Statistics 110- Lecture 4, 5

1. Lecture 4

    Lecture 4는 독립(Independence), 조건부 확률(Conditional Probability)에 대한 내용이다. 개인적으로 조건부 확률의 개념을 설명하는 방식이 굉장히 인상 깊었다.

1) Independence

    Event $A,B$가 식 $P(A \cap B) = P(A) P(B)$를 만족하면 서로 독립(Independent)이라고 한다. Disjoint(서로소)와는 완전히 다른 개념이다. disjoint는 A가 일어나면 B가 일어나지 않는 것이고, 독립은 A가 일어났을 때 B에 대한 정보는 아예 모르는 것을 의미한다.
  만약 사건 3개 $A,B,C$가 있고, 그들이 모두 독립이라면 아래 식들을 모두 충족해야 한다.

• $P(A,B)=P(A)P(B)$
• $P(B,C)=P(B)P(C)$
• $P(A,C)= P(A)P(C)$
• $P(A,B,C) = P(A)P(B)P(C)$

2) Conditional Probability

    조건부 확률은 "기존의 확률에 새로운 정보(증거)가 들어왔을 때 어떻게 확률값을 업데이트할까?"라는 질문에 대한 답을 제공해준다. 식은 아래와 같다.

$P(A|B) = {P(A\cap B) \over P(B)}$ (단, $P(B)$>0)

식은 A given B라고 읽는다. B가 주어졌을 때, A의 확률을 의미한다.

    조건부 확률을 설명하기 위해 강의에서는 두 가지 방식을 사용한다.

i) pebble world

    pebble world 예시부터 살펴보자.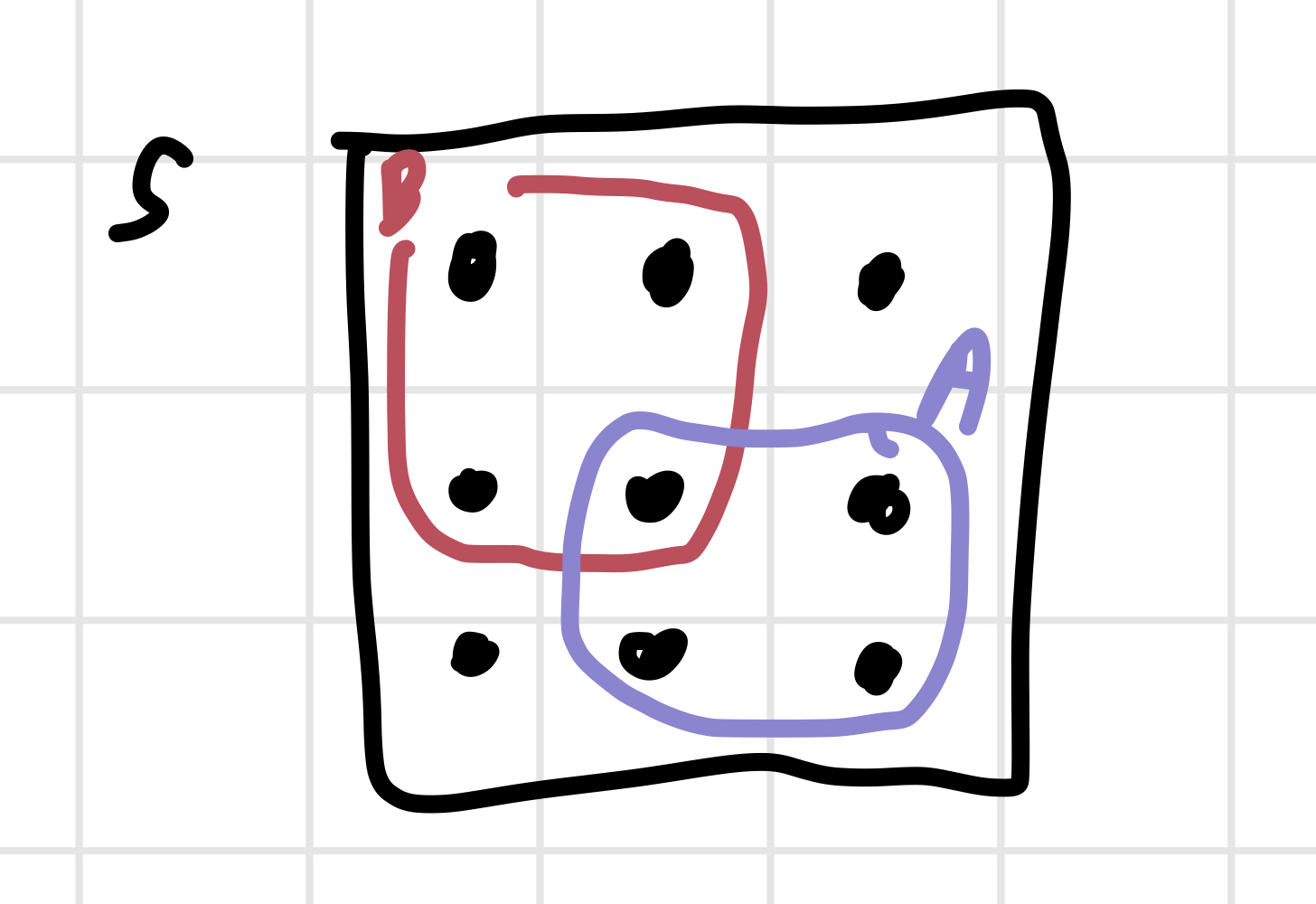
위와 같이 sample space $S$에 9개의 pebble이 있다고 해보자. 사건 $A,B$는 위의 영역과 같다. 전체 mass는 1이다. 이런 상황에서 $P(A|B)$를 구해보자. 사건 $B$가 주어졌을 때 사건 $A$의 확률을 의미하므로, 이 예시에서는 사건 B의 영역에만 집중한다. 즉, 우리가 생각하는 확률의 영역을 빨간 영역으로 제한하겠다는 뜻이다. $S$의 total mass가 1이었다면, 이제 이를 renormalize해 $B$의 영역인 빨강 영역의 total mass를 1로 설정한다. 그 안에서 $A$가 일어날 확률은 0.25가 된다.

ii) frequentist world

    다음은 frequentist world이다. binary 데이터를 생성하는 실험을 여러 번 반복하는 상황이다. 여러 가지 실험 중 사건 B가 일어난 실험들을 동그라미 쳤을 때, 이들 중 A가 발생했을 확률을 구하는 것이 우리의 목표다.
사건 A,B를 정의하진 않았지만, B가 발생한 것들을 동그라미 쳐보았다고 가정하자. 그러면 A가 발생한 확률은 동그라미 친 실험들 내에서만 계산해야 한다는 것이 이 예시의 요지이다.

3) 조건부 확률에 대한 Theorem

• $P(A\cap B)= P(A|B)P(B)= P(B|A)P(A)$
• $P(A_1, A_2, ..., A_n)= P(A_1)P(A_2|A_1)P(A_3|A_1,A_2)...P(A_n|A_1,A_2...A_{n-1})$
• $P(A|B)= {P(B|A)P(A) \over P(B)}$ (Bayes' Rule)

2. Lecture 5

1) Thinking Conditionally

    Conditional Probability 문제를 해결하는 팁에 대한 내용이다.

1) 간단하고 극단적인 예시를 각각 들어보기
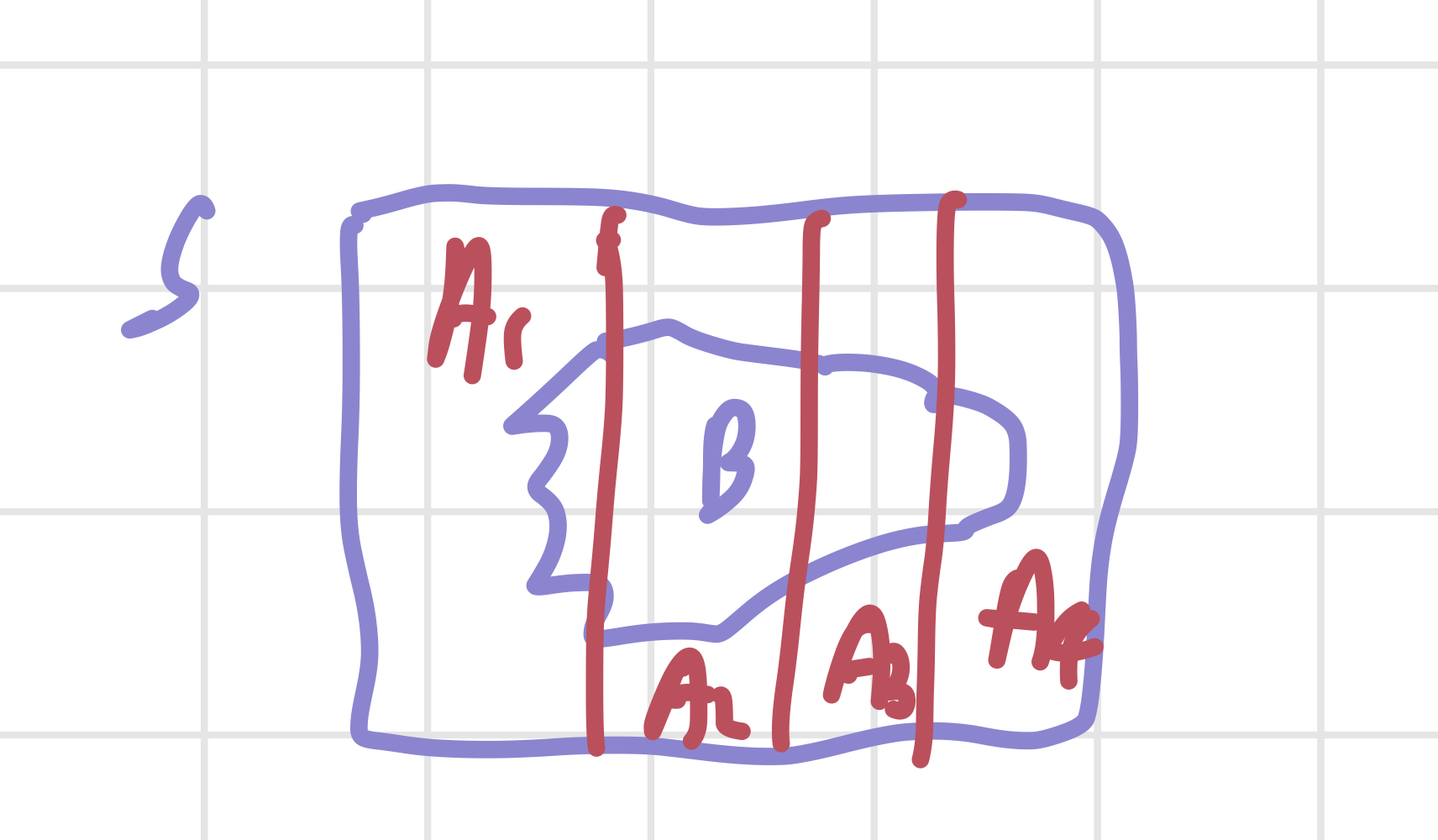
2) 문제를 간단한 여러 개의 문제들로 나눠서 생각하기 (아래 그림 참고)
-> 단, 문제를 나눌 때, 각 문제는 disjoint해야 하고, 나눈 문제들의 합집합은 반드시 S여야 한다.

위에서 2)에 대한 내용은 Law of total probability이다.

2) Law of Total Probability

$P(B) = P(B\cap A_1) + P(B\cap A_2)+... +P(B\cap A_n) = P(B|A_1)P(A_1)+ P(B|A_2)P(A_2)+...+ P(B|A_n)P(A_n)$

위의 그림과 같이 이해하면, B의 영역을 A와 겹치는 부분을 통해 계산할 수 있다. 생각보다 문제 해결에 이 공식이 유용하게 쓰이기 때문에 잘 알아둘 필요가 있다.

예시를 통해 Law of Total Probability가 어떻게 쓰이는지 자세히 살펴보자.

예시 1

  트럼프 카드에서 2장을 뽑을 때, $P(\text{뽑은 2장 중 모두 ace인 경우}|P(\text{뽑은 2장 중에 ace가 있는 경우}), P(\text{뽑은 2장 중 모두 ace인 경우}|P(\text{뽑은 2장 중에 스페이드 ace가 있는 경우})$를 구하는 문제다.

i) $P(\text{뽑은 2장 중 모두 ace인 경우}|P(\text{뽑은 2장 중에 ace가 있는 경우})$는 뽑은 두 장 중에 ace가 있을 때, 2장 모두 ace일 확률을 구하는 문제다.
ii) $P(\text{뽑은 2장 중 모두 ace인 경우}|P(\text{뽑은 2장 중에 스페이드 ace가 있는 경우})$ 는 두 장 중에 스페이드 ace가 있을 때, 2장 모두 ace일 확률을 구하는 문제다.

예시 2

3) Common Mistakes

    조건부 확률에서 흔히 실수할만한 지점들에 대해서 짚고 넘어가려고 한다.

• $P(A|B), P(B|A)$를 정확히 구분하자.
• Prior인 $P(A)$와 posterior인 $P(A|B)$를 정확히 구분하자.
• Independence와 conditional independence를 구분할 것.

위에서 Conditional Independence는 새로 등장한 개념이다.

Conditional Independence

    Event C가 주어졌을 때 Event A,B가 conditionally independent하려면 아래 식을 만족해야 한다. ($P(A,B|C)$는 C가 주어졌을 때 A,B가 동시에 일어날 확률을 의미)

$P(A,B|C) = P(A|C)P(B|C)$

conditionally independent라는 조건이 없다면 위의 식은 약간 다르게 전개된다.

$P(A,B|C) = P(A|B,C)P(B|C) = P(B|A,C)P(A|C)$

왜 이렇게 되는지 증명해보자. 이 식을 이해하면, 위의 conditional independence도 이해하기 쉽다.

이 식에서 C가 주어졌을 때 A,B가 conditionally independent하다면,

$P(A|B,C) = P(A,C)$ 을 만족한다.

이를 위의 식에 대입하면 conditionally independent 할 때의 식을 얻을 수 있다.

* 주의할 점

independent하다고 conditionally independent한 것도 아니고, conditionally independent하다고 independent가 보장되는 것도 아니다.