Statistics 110- Lecture 6, 7

1. Lecture 6

    Lecture 6에서는 Monty Hall problem, Simpson's Paradox에 대해서 이야기 한다. 먼저 Monty Hall 문제부터 살펴보자.

1) Monty Hall Problem

    이 문제는 확률과 통계 강의가 아니더라도 어디선가 한 번쯤은 들어보았을 문제다. 문이 3개가 있는데 그 중 하나의 문 뒤에는 차가, 두 개의 문 뒤에는 염소가 있다. Monty라는 사람이 진행자인데, 만약 내가 3개의 문 중 차가 있는 문을 연다면 차를 경품으로 주는 설정이다. 편의상 각 문을 1번~3번이라고 번호를 붙여서 이야기하겠다. 게임의 진행 방식은 아래와 같다.

1. 내가 3개의 문 중 하나를 고른다. (1번을 골랐다고 예시를 들어보자.)
2. 그러면 Monty는 2,3번 중에 염소가 있는 하나의 문을 열고, 나에게 문을 바꿀 것인지 물어본다.

이러한 상황일때, 처음에 1번을 고른 나는 문을 바꾸는 것이 좋을까 아니면 선택을 그대로 유지하는 것이 좋을까?

이 문제를 확률적으로 계산해서 어떤 선택을 하는 것이 좋을지 알아보자는 것이다.

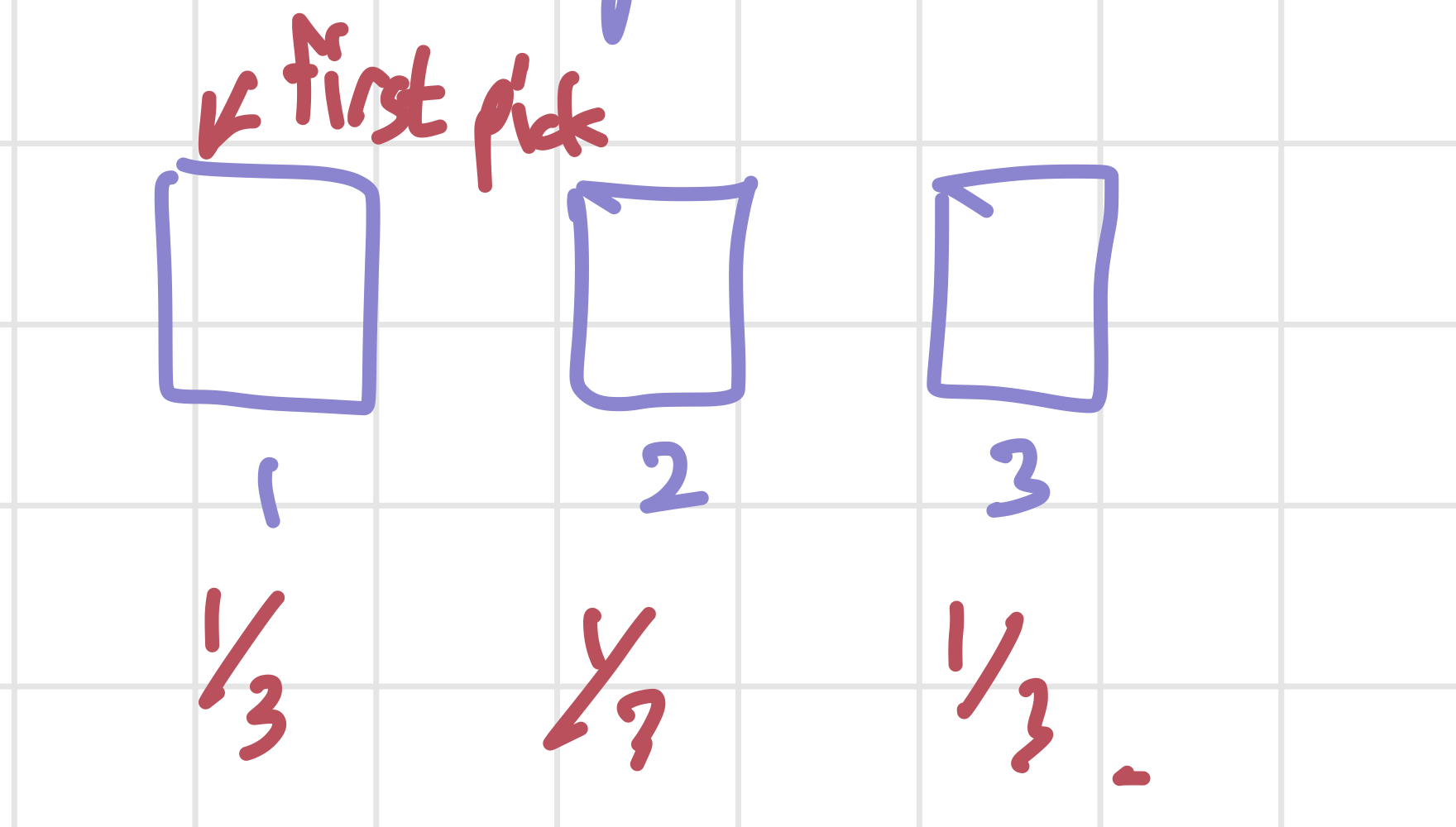
일단 처음 상황은 위의 사진과 같다. 내가 각 문을 고를 확률은 모두 1/3이다.(예시로 1번문을 골랐다고 가정하자.) 그리고 나서 Monty가 2번 문을 열었다고 하면, 우리는 Monty가 2번 문을 선택했다는 사실과 2번 문 뒤에 염소가 있다는 사실을 알고 있다. 강의는 이 문제를 3가지 방법으로 해결한다.

i) 가지치기(?)

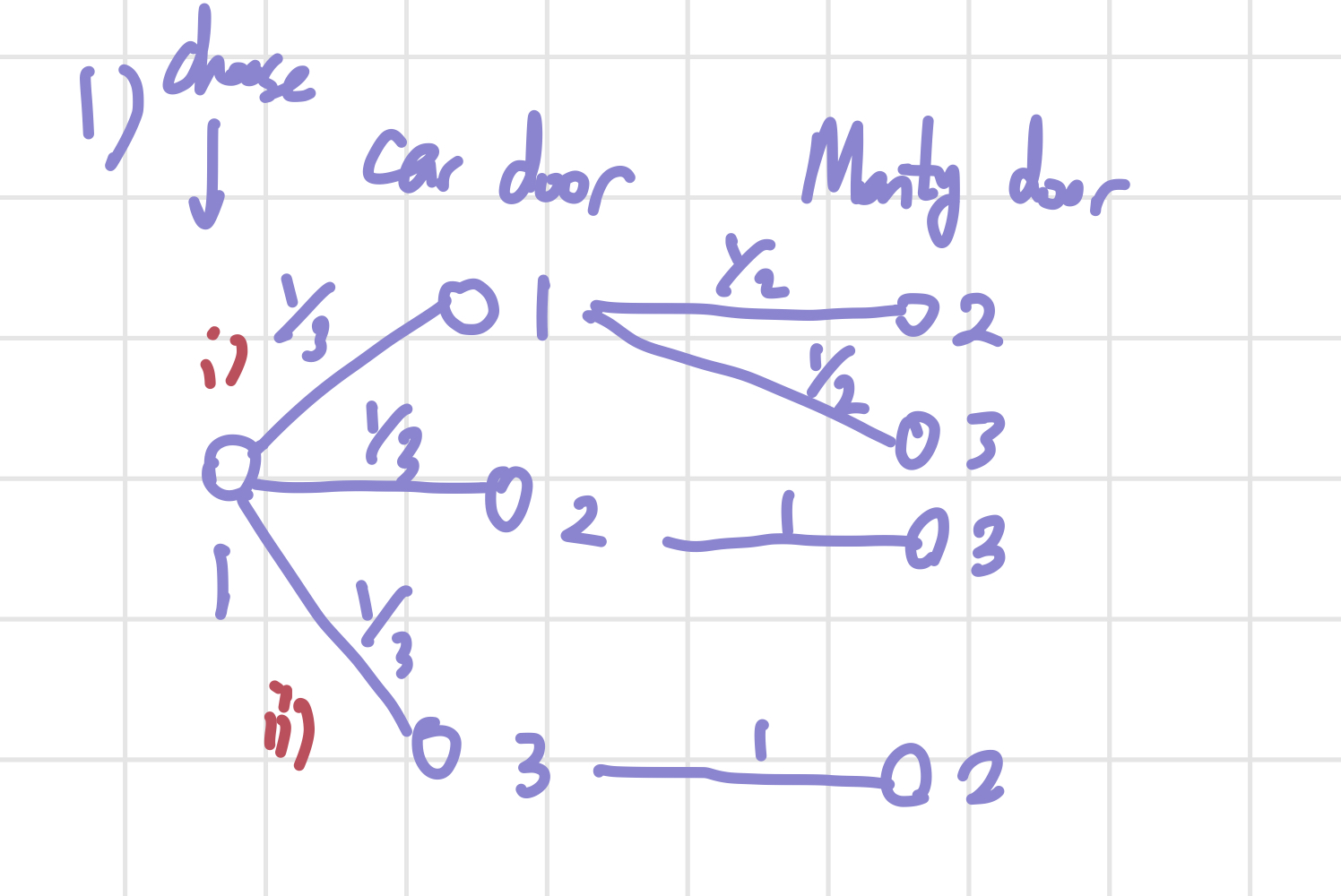
  첫 번째 예시는 가지치기 그림을 그려서 해결하는 방식이다. 경우의 수를 처음 배울 때 접한 그림인 것 같기도 하다. 위의 그림의 왼쪽부터 내가 고른 문, 차가 있는 문, Monty가 열어준 문의 번호를 쓴 것이다. 예를 들어 i)의 가지는 내가 1번 문을 고르고, 차가 있는 문은 1번이어서 Monty가 2번을 연 경우를 나타내는 것이다.
  Monty가 2번 문을 연 경우를 보자. i)번 길은 1/6의 확률을, ii)번 길은 1/3의 확률을 가진다. 우리는 Monty가 2번 문을 여는 경우만 생각하고 있으므로, i),ii)의 경우를 renormalize해보자. 조건부확률을 공부할 때의 pebble world 예시처럼 우리가 구하려는 확률과 관계 없는 것들을 제거하는 과정인 셈이다. i), ii)번 경우의 확률의 합이 1이 되게 renormalize하면 i)번 경우는 1/3, ii)번 경우는 2/3이 된다.
  이제 우리가 구하려는, $P(\text{success if switch}| \text{Monty opens door 2})$를 구해보자. 2번 문을 Monty가 열었을 때 내가 고른 문을 바꿔서 성공하는 경우는 ii)번 뿐이다. 따라서 $P(\text{success if switch}| \text{Monty opens door 2})= {2 \over 3}$ 이 된다. 만약 내가 2번문을 처음에 고르고, Monty가 1번 문을 열었다고 해도 위의 그림과 같이 가지치기를 통해 확률을 구할 수 있다.

ii) LOTP (Law of Total Probability)

    다음으로는 LOTP이다. 이전 글에서도 정리한 적 있는 개념이다. 위의 경우와 마찬가지로 우리가 처음 고른 문은 1번이라고 가정한다. 들어가기에 앞서 우리가 사용할 event를 정의하자. $S$는 우리가 1번 문을 처음에 고르고, 선택을 바꾼다고 가정했을 때 성공하는 경우를, $D_j, j \in\{1,2,3\}$는 $j$번 문 뒤에 차가 있는 경우를 나타낸다. 이렇게 정의하는 경우, 우리가 구하고자 하는 확률은 $P(S)$가 된다. 이를 LOTP를 통해 구하겠다는 것이다. 이전 글에서도 언급했듯이, LOTP는 하나의 확률을 서로소인 확률, 즉 교집합이 없는 확률들로 쪼개서 구하는 방법이다. 따라서 $P(S)$를 이에 맞게 구하면 아래처럼 식을 쓸 수 있다.

$P(S)= P(S|D_1)\times {1 \over 3}+ P(S|D_2)\times {1 \over 3}+P(S|D_3)\times {1 \over 3}$

위의 식에서 1/3씩 곱하는 이유는 1번 문을 고를 확률을 적용해주어야 하기 때문이다. 이를 계산하면, 아래와 같이 식을 정리할 수 있다.

$P(S)= P(S|D_1)\times {1 \over 3}+ P(S|D_2)\times {1 \over 3}+P(S|D_3)\times {1 \over 3}$
= $0 + 1 \times {1 \over 3} + 1 \times {1 \over 3}$
= $2 \over 3$

해설을 조금 덧붙이자면, $P(S|D_1)$는 우리가 1번 문을 골랐을 때 차는 1번 문 뒤의 있고, 문을 바꾼 경우를 의미한다. 따라서 성공할 확률은 0이 되는 것이다. 나머지도 이와 같이 생각하면 된다.

    LOTP를 사용해도 가지치기와 같이 $2 \over 3$이 나온다.

iii) Extreme Case

    마지막으로, 구체적인 확률이 아닌 직관을 이용해 생각하는 방법이다. 만약 문의 개수가 3개가 아니라 10000개라면, 우리는 문을 쉽게 바꿀 것이다. 이는 문이 3개일 때도 동일하게 적용될 것이다. 문을 바꾸는 것이 차가 있는 문을 고를 확률을 높여주는 것이다.

2) Simpson's Paradox

    다음으로 살펴볼 확률 문제는 Simpson's Paradox라는 문제이다. 기본적인 문제의 조건은 아래 그림과 같다. 두 명의 의사 Hibbert와 Nick이 있고, 이 의사들이 각각 2개의 수술(심장 수술(heart), 반창고를 붙이는 수술(bandaid))을 진행한다.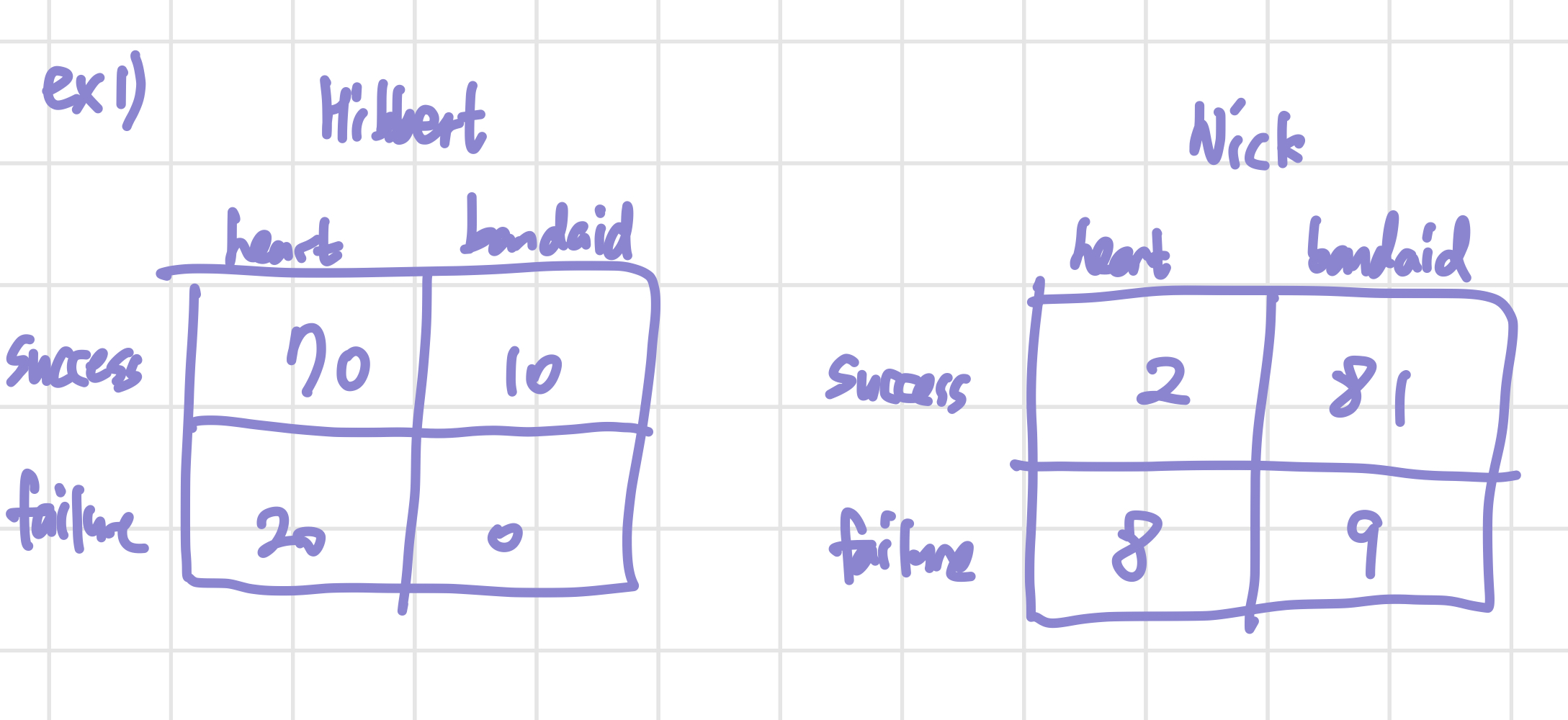
위 그림에 적혀 있는 숫자는 수술의 횟수이다. Hibbert의 경우, 심장 수술을 70번 성공하고 20번 실패했다는 것을 알 수 있다. 전체적인 성공률을 보면, Hibbert는 80%, Nick은 83%의 성공률을 가지고 있다. 이렇게 봐서는 둘 중에 수술 받을 의사를 고르라면 Nick을 고르는 것이 당연해보인다. 그러나 심장 수술과 bandaid 수술을 나누어서 확률을 계산하면 이와 다른 판단을 하게 된다.
  이것도 일종의 conditional thinking이라고 볼 수 있는데, 심장 수술과 bandaid를 따로 생각하는 경우, 모두 Hibbert의 성공률이 Nick보다 높다. 이를 식으로 표현해보자.

• $A$: 수술을 성공하는 경우
• $B$: Nick에게 수술을 받는 경우 ($B^C$는 Hibbert에게 수술을 받는 경우)
• $C$: 심장 수술을 받는 경우 ($C^C$는 bandaid 수술을 받는 경우)

• $P(A|B,C)< P(A|B^C,C)$ ($P(A|B,C)$는 $B,C$가 일어났을 때, A의 확률을 의미)
  -> (Nick이 심장 수술을 할 때 성공할 확률) < (Hibbert가 심장 수술을 할 때 성공할 확률)
• $P(A|B,C^C)< P(A|B^C,C^C)$
  -> (Nick이 bandaid 수술을 할 때 성공할 확률) < (Hibbert가 bandaid 수술을 할 때 성공할 확률)

위의 두 부등호 식을 더하면 각 의사별 전체 수술 성공률을 얻을 수 있다. 부등식의 계산에서도 많이 봤듯이, 부등호 방향이 같은 두 식을 더하면 부등호 방향도 같을 것 같지만, 이 경우에서는 그렇지 않다는 것이 Simpson's Paradox에서 이야기하는 내용이다.

$P(A|B,C)+P(A|B,C^C)< P(A|B^C,C)+P(A|B^C,C^C)$
$= P(A|B)<P(A|B^C)$일 것 같지만, 실제로는
$P(A|B)>P(A|B^C)$

    왜 이런 현상이 생길까? LOTP를 이용해 식을 전개하면 아래와 같다. (어려워보이지만, given B를 나타내는 $'|B'$만 식에서 없애면 우리가 원래 알고 있는 LOTP와 동일학다.)

$P(A|B) = P(A|B,C)P(C|B) + P(A|B,C^C)P(C^C|B)$

위의 식에서 $P(A|B,C)<P(A|B^C,C), P(A|B,C^C)<P(A|B^C,C^C)$ 이다. 그러면 부등호의 방향에 영향을 주는 것은 $P(C|B), P(C^C|B)$ 인 것이다. 그러나 부등호가 바뀌는 이유가 이 두 개의 일종의 weight라는 것을 직접적으로 증명하기는 쉽지 않다.

2. Lecture 7

    다음은 Lecture 7의 내용이다. Random Variable에 대해서 간단히 알아보자. 그 전에 강의에서 Gambler's Ruin이라는 문제를 소개하는데, 계산을 그냥 쭉 하는 내용이라 내가 필기한 것만 올려놓겠다.

1) Random Variable

    Random Variable은 Sample Space $S \rightarrow \mathbb{R}$를 mapping하는 함수이다. 아래 그림을 보면 이해하기 조금 편할 것 같다.

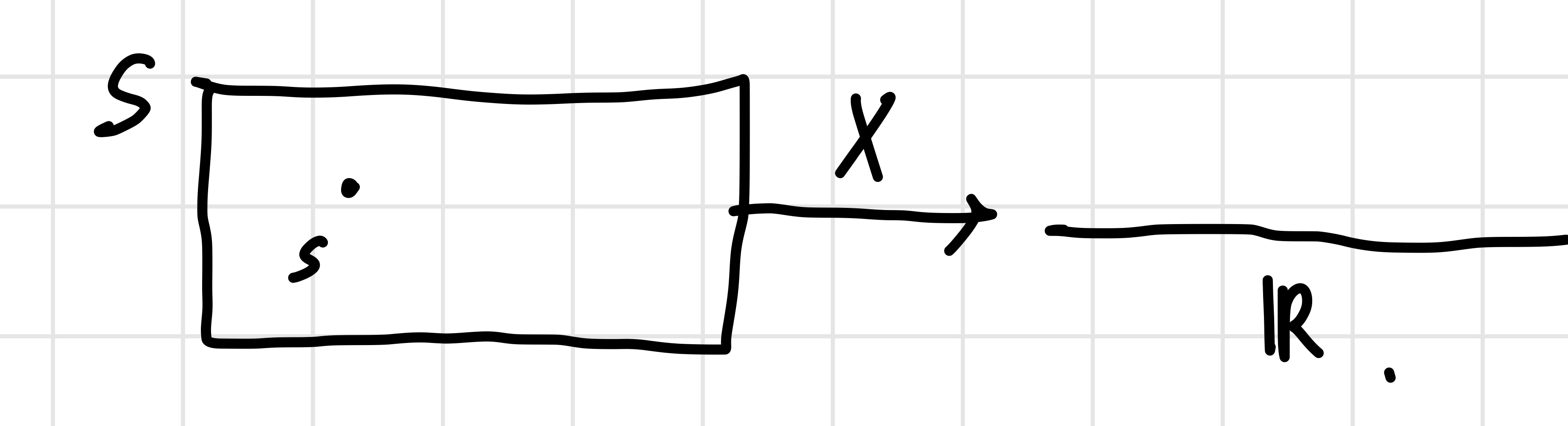
특정 실험의 numerical summary라고도 해석할 수 있다. 이때, S는 특정 실험의 결과이다. Random variable과 그 분포를 파악하는 것은 굉장히 중요하고, 자주 나온다. 대표적인 Random Variable들을 알아보자. 아마 8강까지 Random variable에 대한 내용이 이어질 것 같다.

i) Bernoulli Distribution

    random variable $X$가 Bernoulli Distribution을 가지려면 다음 조건들을 만족해야 한다.

• 2개의 value (0,1/성공,실패)만 값으로 가져야 한다.
• $P(X=1)= p, P(X=0)=1-p$

이때, $X=1$은 event에 해당한다. 보통 distribution을 표기할 때 아래와 같이 표기한다.

$X \sim \mathrm{Bern}(p)$

뒤에 나올 Binomial Distribution과 Bernoulli Distribution의 다른 점이 무엇인지 아는 것이 굉장히 중요한데, 차이는 바로 시행 횟수에 있다. Bernoulli는 한 번 시행하는 것이고, Bernoulli를 여러 번 시행하면 Binomial Distribution이라고 부른다.

ii) Binomial Distribution

    Binomial Distribution은 $X \sim \mathrm{Bern}(p)$을 n번 시행할 때, 성공하는 횟수를 나타내는 분포다. 표기는 아래와 같이 한다.

$X \sim \mathrm{Bin}(n,p)$

시행을 n번하기 때문에, 분포를 식으로 표현할 수 있다.

$P(X=k)= {n \choose k} p^k(1-p)^{n-k}$ , $0\leq k\leq n, k$는 정수.

추가로, 두 개의 Binomial Distribution $X \sim \mathrm{Bin}(n,p), Y \sim \mathrm{Bin}(m,p)$가 있고, 독립 관계일 때, $X+Y \sim \mathrm{Bern}(n+m,p)$ 가 성립한다.