
- 윤덕호 저서 파이썬 날코딩으로 알고 짜는 딥러닝을 공부하고 개인적으로 정리한 글입니다.
- 사진, 내용, 코드는 책을 참고한 것입니다. 코드는 오픈소스로 저저의 깃허브에 모두에게 공개되어있습니다.
- Ch1 - 단층퍼셉트론(SLP)의 코드를 재활용 했습니다.
이진 판단 문제의 신경망 처리
- 가중치와 편향을 이용하는 퍼셉트론의 선형 연산은 1, 0 두 가지 값으로 결과를 제한할 수 없음, 이 때문에 신경망은 확률값을 추정하고 역치를 두어 1과 0으로 분류하는 아이디어가 제시 되었지만, 퍼셉트론의 선형 연산은 출력범위를 제한하는 것마저 불가능함
- 따라서 실숫값을 생산하고 이를 확률값의 성질에 맞게 변환해주는 비선형 함수를 찾았고, 이것의 한 예가 시그모이드 함수임
- 시그모이드 함수를 이용해 신경망 출력을 확률로 해석하고도 어떻게 학습을 해야하는지가 문제였음 (손실함수의 정의가 어려웠기 때문에)
- 이는 교차 엔트로피라는 개념을 통해 해결됨 (두 확률 분포가 얼마나 다른지)
- 챕터 1에서 사용한 코드를 재활용함
시그모이드 함수
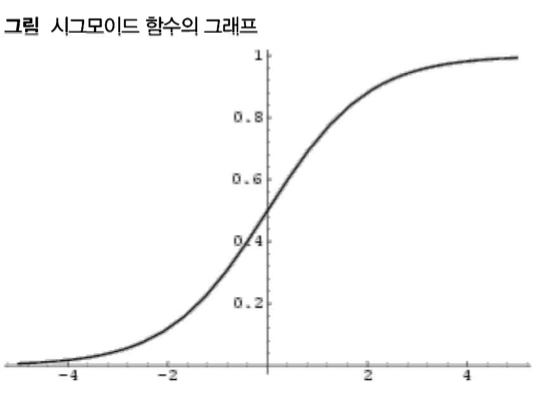
-
시그모이드 함수 (Sigmoid Function)은 범위에 제한 없는 임의의 실숫값을 입력으로 받아 확률값의 범위에 해당하는 0과 1 사이의 값을 출력하는 함수이며 위와 같이 표기한다.
-
입력값 x를 logit값으로 변환해주는 함수
-
넓은 범위의 값을 간단히 표현할 수 있고 변화량보다는 변화 비율 관점에서 더 민감하게 포착할 수 있음
-
답이 참일 가능성을 로짓으로 표현한 값, 상대적인 가능성을 로그를 이용해 나타낸 값
-
시그모이드 함수의 미분
확률 분포와 정보 엔트로피
-
분자들의 무질서도 혹은 에너지의 분산 정도를 나타내는 물리학 용어에서 기원
- 예시로 라면 2비트(00,01,10,11)로 구별 하고 이면 2비트(00,01,10)를 사용하겠지만 용량낭비가 발생함(11)
- 이와 같은 사건이 k 차례 일어난다면 경우의 수는 가되고 이를 표현 하기 위해선 비트의 경우의 수 가 되어야 함 이는 결국 으로 나타남
- 따라서 일 때 한 사건을 표현하는데 최소 필요한 비트 수는 이며 이 값을 정보량이라고 함
-
이러한 정보량 개념은 균일하지 않은 확률 분포에도 확장해서 적용할 수 있고, 가중평균으로 적용 이라면
-
허프만 코드: 표현하려는 대상의 분포 비율을 조사해 자주 나타나는 대상에는 짧은 이진 코드를, 가끔 등장하는 코드에는 긴 이진 코드를 할당해 전체 표면에 필요한 비트수를 줄여주는 정보 압축 기법
-
정보 엔트로피는 어떤 확률 분포로 일어나는 사건을 표현하는데 필요한 정보량이며 이 값이 커질수록 확률 분포의 불확실성이 커지며, 예측이 어려워짐
확률 분포의 추정과 교차 엔트로피
- 앞서 언급한 정보 엔트로피 H 는 결국 정보량의 기대값(가중평균)이라고 볼 수 있음
- 교차 엔트로피는 정보량을 제공하는 확률분포와 가중평균에 사용되는 확률 분포를 서로 다르게 설정하여 정보량의 기댓값을 구함
- 즉 확률 분포 Q에 따른 정보량을 갖는 사건이 확률 분포 P에 따라 일어날 때를 의미함
- 언제나 H(P,Q) >= H(P,P)가 성립하며 등호는 두 분포가 일치할 때만 성립함
- 결국 두 확률 분포가 얼마나 다른지를 나타내는 정량적 지표
딥러닝 학습에서의 교차 엔트로피
-
수시로 수정되는 딥러닝 모델의 추정 확률 분포 P 그리고 딥러닝 모델이 흉내 내야 할 미지의 확률 분포 Q가 있다면 P와 Q의 교차 엔트로피 값을 추정하여 작아지는 쪽으로 P를 수정시킴
- 문제1: 확률 분포 Q를 정확하게 알 수 없음
- 문제2: 학습에 이용되는 데이터들은 각각 다른 입력과 그에 따른 출력이기 때문에 확률 분포 Q는 고정된 확률 분포가 아닌 입력에 따라 그때 그때 달라지는 조건부 확률 분포임
-
레이블 정보의 내용을 추정 확률 분포 P가 접근해야할 학슴 목표, 입력에 대한 출력의 조건부 확률 분포로 간주하면 교차 엔트로피 계산이 가능함
-
딥러닝 학습의 궁극적인 목표는 새로운 입력에 대해서도 유사한 문제 풀이 경험을 토대로 알맞은 답을 내놓는 것
-
이진 판단 딥러닝에서는 입력에 대해 직접 출력을 추정하지 않으나 출력의 확률분포, 즉 입력에 따른 조건부 확률 분포로서 추정함
시그모이드 교차 엔트로피와 편미분
-
이진 판단 문제의 정답 z가 주어지면 참일 확률은 p_t, 거짓일 확률은 p_f 일 때 p_f = 1-z임을 나타냄. 보통 z 는 0 혹은 1로 주어짐
-
신경망 회로의 출력이 로짓값x로 계산되었다고 할 때 이에 대응하는 확률값은 q_t = sigmoid(x), q_f = 1 - sigmoid(x)
-
여기서 교차 엔트로피 정의식에 대입하면
-
-
x가 양수일 때는 안정적으로 잘 계산되지만 음수일 때 e^(-x)가 폭주하는 오류가 발생
-
이진 판단 문제는 0 혹은 1값 -> z를 0, 1
-
여기서 교차 엔트로피의 편미분을 진행하면
계산값 폭주 문제와 시그모이드 관련 함수의 안전한 계산법
-
파이썬 내에서 sigmoid(-1000) 계산 문제가 발생함. e^1000은 지나치게 큰 값이어서 inf로 표현되고 이는 오버플로 오류가 나타남
-
이에 대한 해결책은 음수일 경우 계산 방법을 다르게 처리하는 방법이 있음: e^(-x)가 e^(x)로 연산 되도록
-
하지만 일괄 처리를 해야하기 때문에 조건문을 통해 하나하나 바꾸는 것은 적합하지 않으며, 반복문을 통해 원소별 부호 검사하는 방법 또한 효율적이지 않음, 다음 수식을 적용하면 x의 부호에 따라 식이 다르게 적용되는것을 확인할 수 있음
구현코드 및 Annotation
이진 판단: 천체의 펄서 여부 판정 신경망
- 천체가 펄서인지 아닌지 판정하는 이진 판단 신경망
- 단층 퍼셉트론
- 이진 판단 문제와 시그모이드 함수
- Data : Pulsar Data (Kaggle)
- 17898개의 천체(rows)
- 8가지의 특성(columns) = integrated profile과 DM-SNR curve 값에 대한 평균, 표준편차, 첨도, 뒤틀림 등
- 펄서의 여부(target)
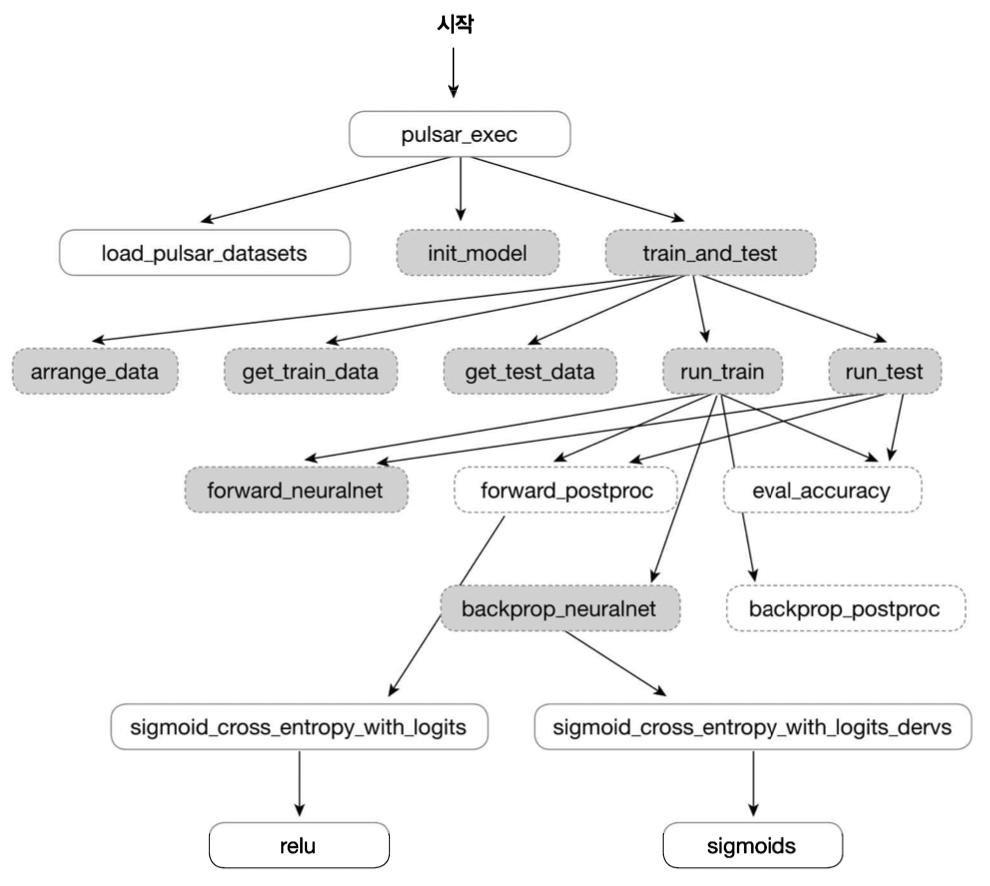
- 점선은 Ch1 - 단층퍼셉트론(SLP) 에서 사용된 함수들을 그대로 사용한다는 의미 | 실선은 새롭게 선언
- 구현 코드 파일 실행
%run ../ch01/단층퍼셉트론(SLP).ipynb- 메인 함수 정의
def pulsar_exec(epoch_count=10, mb_size=10, report=1):
load_pulsar_dataset()
init_model()
train_and_test(epoch_count, mb_size, report)- 데이터 적재 함수의 정의
def load_pulsar_dataset():
with open('.../Study/파이썬 날코딩으로 알고 짜는 딥러닝/data/pulsar_stars.csv') as csvfile:
csvreader = csv.reader(csvfile)
next(csvreader, None) # 첫 행을 읽지 않고 건너뜀
rows = []
for row in csvreader:
rows.append(row)
global data, input_cnt, output_cnt
input_cnt, output_cnt = 8, 1
data = np.asarray(rows, dtype='float32')- 후처리 과정에 대한 순전파와 역전파 함수의 재정의
def forward_postproc(output, y): # 순전파 처리 수행
# 두 행렬의 각 원소 짝에 대한 시그모이드 교차 엔트로피를 일괄적으로 구함
entropy = sigmoid_cross_entropy_with_logits(y, output)
# 이들의 평균 = loss
loss = np.mean(entropy)
return loss, [y, output, entropy]
def backprop_postproc(G_loss, aux):
y, output, entropy = aux
# 순전파는 entropy -> loss였음, 따라서 역전파는 loss -> entropy
# 1.0을 행렬의 원소 수로 나누어 각 원소의 손실 기울기로 부여
g_loss_entropy = 1.0 / np.prod(entropy.shape)
# y와 output 쌍 간의 시그모이드 교차 엔트로피 편미분 값을 구함
g_entropy_output = sigmoid_cross_entropy_with_logits_derv(y, output)
#역전파 결과를 산출
G_entropy = g_loss_entropy * G_loss
G_output = g_entropy_output * G_entropy
return G_output- 정확도 계산 함수의 재정의
def eval_accuracy(output, y):
# output의 부호에 따라서 신경망의 판단을 알 수 있음(시그모이드를 안써도됨)
estimate = np.greater(output, 0)
# 정답은 1 or 0 , 안전하게 0.5와 비교하여 구함
answer = np.greater(y, 0.5)
# 불리언값 배열로 비교
correct = np.equal(estimate, answer)
# 평균을 내면 결국 불리언이 1,0으로 간주되어 계산됨
return np.mean(correct)- 시그모이드 관련 함수 정의
def relu(x): # x배열 원소 각각에 대해 음수는 모두 0으로 대치하는 함수
# np.max는 문자열 전체와 0을 비교하는 것이어서 다름
return np.maximum(x, 0)
def sigmoid(x):
return np.exp(-relu(-x)) / (1.0 + np.exp(-np.abs(x)))
def sigmoid_derv(x, y): # 시그모이드 미분 수식 원리 이해는 위 수식 참고
return y * (1 - y)
def sigmoid_cross_entropy_with_logits(z, x):
return relu(x) - x * z + np.log(1 + np.exp(-np.abs(x)))
def sigmoid_cross_entropy_with_logits_derv(z, x):
# 시그모이드 교차엔트로피 편미분 수식 원리 이해는 위 수식 참고
return -z + sigmoid(x)모델의 확장
-
예측 데이터 셋은 타겟이 불균형함 -> 별과 펄서가 비슷한 수가 되도록 데이터의 비율을 바꾸어 출연빈도가 낮은 펄서를 학습하는 기회를 늘리는 것
-
별 데이터를 버리는 방법, 펄서를 중복사용하는것(잡음 주입하면 성능이 좋아질수도)
-
하지만 이런 방법은 신경망 추정 성능은 향상될 수 있지만 겉보기 정확도는 오히려 하락할 가능성이 있다.
-
이에 대한 다른 평가지표로 정밀도(precision)와 재현율(recall)이 있다.
- 정밀도: 참으로 예 추정한 것 중 참인 것의 비율
- 재현율: 정답이 참인 것들 가운데 참으로 추정한 것의 비율
- F1 score: 정밀도 재현율의 조화 평균
-
결론적으로 확장된 코드에는 펄서의 수를 늘린 데이터 사용, 평가지표에 정밀도, 재현율,F1값 추가가 포함되어 있다
- 짜놓은 이진판단 코드 재활용
%run ../ch02/이진판단.ipynb- 메인함수 재정의 (adjust_ratio 파라미터 추가)
def pulsar_exec(epoch_count=10, mb_size=10, report=1, adjust_ratio=False):
load_pulsar_dataset(adjust_ratio)
init_model()
train_and_test(epoch_count, mb_size, report)- 데이터 적재함수 재정의 (adjust_ratio 파라미터 추가)
def load_pulsar_dataset(adjust_ratio):
pulsars, stars = [], []
with open('.../Study/파이썬 날코딩으로 알고 짜는 딥러닝/data/pulsar_stars.csv') as csvfile:
csvreader = csv.reader(csvfile)
next(csvreader, None)
rows = []
#펄서와 별의 데이터를 나누어 담는다
for row in csvreader:
if row[8] == '1': pulsars.append(row)
else: stars.append(row)
global data, input_cnt, output_cnt
input_cnt, output_cnt = 8, 1
star_cnt, pulsar_cnt = len(stars), len(pulsars)
#매개 변수 값이 True인 경우
if adjust_ratio:
#별의 두배 길이로 데이터를 만들고
data = np.zeros([2*star_cnt, 9])
#별 데이터를 넣어줌
data[0:star_cnt, :] = np.asarray(stars, dtype='float32')
#반복문을 통해서 별데이터와 같은 수 만큼 펄서 데이터를 넣어 줌
for n in range(star_cnt):
data[star_cnt+n] = np.asarray(pulsars[n % pulsar_cnt], dtype='float32')
#매개변수 값이 False인 경우 불균형에 대한 고려 없이 별과 펄서 데이터를 넣어줌
else:
data = np.zeros([star_cnt+pulsar_cnt, 9])
data[0:star_cnt, :] = np.asarray(stars, dtype='float32')
data[star_cnt:, :] = np.asarray(pulsars, dtype='float32')- 정확도 계산 함수 재정의
def eval_accuracy(output, y):
# Confusion Matrix
est_yes = np.greater(output, 0)
ans_yes = np.greater(y, 0.5)
est_no = np.logical_not(est_yes)
ans_no = np.logical_not(ans_yes)
# precision recall f1 score을 위한
tp = np.sum(np.logical_and(est_yes, ans_yes))
fp = np.sum(np.logical_and(est_yes, ans_no))
fn = np.sum(np.logical_and(est_no, ans_yes))
tn = np.sum(np.logical_and(est_no, ans_no))
accuracy = safe_div(tp+tn, tp+tn+fp+fn)
precision = safe_div(tp, tp+fp)
recall = safe_div(tp, tp+fn)
f1 = 2 * safe_div(recall*precision, recall+precision)
return [accuracy, precision, recall, f1]
def safe_div(p, q):
#타입 오류 방지를 위한 형변환
p, q = float(p), float(q)
#0 나누기 오류를 방지하는 예외 처리
if np.abs(q) < 1.0e-20: return np.sign(p)
return p / q- 학습 및 평가 함수 재정의(출력 부분) (단층 퍼셉트론 파트에 있는 함수)
def train_and_test(epoch_count, mb_size, report):
step_count = arrange_data(mb_size)
test_x, test_y = get_test_data()
for epoch in range(epoch_count):
losses = []
for n in range(step_count):
train_x, train_y = get_train_data(mb_size, n)
loss, _ = run_train(train_x, train_y)
losses.append(loss)
if report > 0 and (epoch+1) % report == 0:
acc = run_test(test_x, test_y)
acc_str = ','.join(['%5.3f']*4) % tuple(acc)
print('Epoch {}: loss={:5.3f}, 정확도:{}|정밀도:{}|재현율:{}|F1 Score:{}'. \
format(epoch+1, np.mean(losses), acc_str.split(',')[0],acc_str.split(',')[1],acc_str.split(',')[2],acc_str.split(',')[3]))
acc = run_test(test_x, test_y)
acc_str = ','.join(['%5.3f']*4) % tuple(acc)
print('\nFinal Test: final result = 정확도:{}|정밀도:{}|재현율:{}|F1 Score:{}'.format(acc_str.split(',')[0],acc_str.split(',')[1],acc_str.split(',')[2],acc_str.split(',')[3]))