단층퍼셉트론(Softmax - 선택분류)

DonghyunAnn·2021년 12월 29일

딥러닝

파이썬 날코딩으로 알고 짜는 딥러닝

목록 보기

3/5

윤덕호 저서 파이썬 날코딩으로 알고 짜는 딥러닝을 공부하고 개인적으로 정리한 글입니다.
사진, 내용, 코드는 책을 참고한 것입니다. 코드는 오픈소스로 저저의 깃허브에 모두에게 공개되어있습니다.
Ch1 - 단층퍼셉트론(SLP)의 코드를 재활용 했습니다.

선택 분류 문제의 신경망 처리

이진분류는 후보가 하나, 선택분류는 후보가 여러개인 것의 차이
이진 판단에서처럼 각 후보 항목에 대한 로그 척도와 상대척 추천 강도, 즉 로짓값을 추정하도록 구성되며 이때 퍼셉트론 하나가 후보 하나에 대한 로짓값을 출력함
선택 분류에서 로짓값은 각 후보 항목을 답으로 추정할 확률
- ex: A 항목의 로짓 값 = 3, B 항목의 로짓 값 =1이면 A를 답으로 추정할 확률이 e^(3-1)= 7.39배 만큼 큰 것
로짓값 만으로는 학습 방법을 찾기 어렵고 이에 대한 해결책이 교차 엔트로피에 대한 개념임(챕터2의 시그모이드 교차 엔트로피), 이를 선택분류 문제에도 똑같이 적용
복수의 후보 항목들에 대한 로짓값 벡터를 확률 분포 벡터로 변환하는 함수와 이렇게 구해진 확률 분포와 정답에 나타난 분포간의 교차 엔트로피를 계산하는 함수가 필요함
이는 소프트맥스와 소프트맥스 교차 엔트로피 함수라고 볼 수 있음
따라서 챕터1에서 사용한 코드들을 재활용함

소프트맥스 함수

\frac {e^{x_i}} {e^{x_1} + ... + e^{x_n}}

로짓값 벡터를 확률 분포 벡터로 변환해주는 비선형 함수
27개의 칼럼 데이터 벡터가 input 되면 미니배치 사이즈 N을 고려 했을 때
- 입력은 (N,27)
- 퍼셉트론은 타겟에 근거하여 7개 즉 계산을 위해 (27,7)이 되어
- 최종적으로 (N,7)의 로짓값 벡터가 출력됨
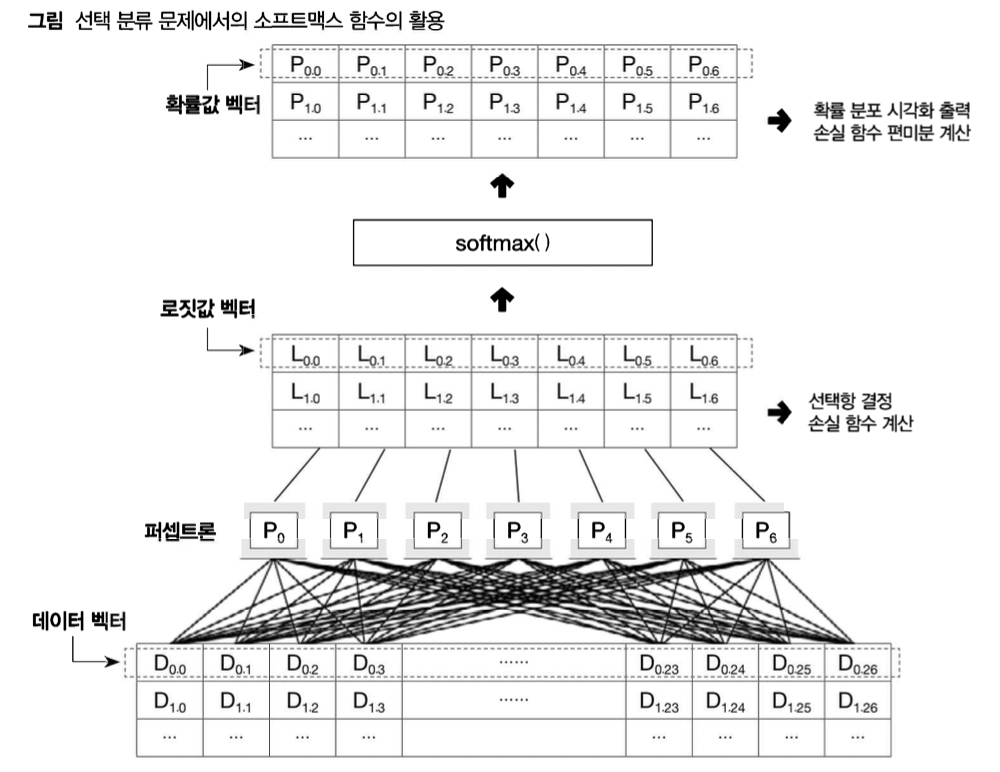
로짓값들은 후보 항들에 대한 선택 확률을 로그 척도로 표현한것, 따라서 굳이 로그 계산을 하지 않아도 최대항만 파악된다면 신경망이 채택할 후보를 바로 알 수 있음
선택 분류를 위한 손실 함숫값도 로짓값 벡터를 이용하여 계산할 수 있음, 즉 굳이 확률값 변환 없이도 순전파의 모든 처리가 가능함
하지만 사용자가 확률 분포를 눈으로 확인하기 위해 필요하며, 역전파 과정에서 손실함수에 대한 편미분을 구할 때 확률분포가 필요함
위 두가지 이유 때문에 로짓값 벡터를 확률 분포 벡터로 변환해 주는 소프트맥스 함수가 필요함
계산 과정에서 오류가 발생할 수 있기 때문에 약간은 변형된 식을 사용한다

소프트맥스 함수 일반식 도출

로짓값 벡터가 주어진다면 (2.0,1.0,1.2,0.7) 이는 $e^{2.0}:e^{1.0}:e^{1.2}:e^{0.7} = 7.39:2.72:3.32:2.01 = 0.479:0.176:0.251:0.130$ 이라는 확률 비율로 변환할 수 있다.
이 내용을 수식으로 변환했을 때 입력벡터 $x_1,...,x_n$ 의 각 $x_i$ 로짓 값에 대응하는 실제 확률값은 $e^{x_i}$ 에 비례하는 값이며 비례 상수를 a라고 하면 $ae^{x_i}$ 이 되고 전체 경우의 확률 합은 1이 되어야 함 $ae^{x_1}+ ... +ae^{x_n} = 1$ 이고 따라서 $a = \frac{1}{ae^{x_1}+ ... + .ae^{x_n}}$ 이 됨
즉 소프트맥스 함수는 입력 벡터 $(x_1,...,x_n)$ 에 대해 $(\frac {e^{x_1}} {e^{x_1} + ... + e^{x_n}}, ... , \frac {e^{x_n}} {e^{x_1} + ... + e^{x_n}})$ 을 출력한다

소프트 맥스 변형식 도출

\frac {e^{x_i-x_k}} {e^{x_1-x_k} + ... + e^{x_n-x_k}}

범위 제약이 없는 x_i의 값은 오버플로 오류를 일으킬 수 있기 때문에 변형식이 필요함
$max(x_i) = x_k$ 일 때 정의식에서 분자와 분모를 동시에 $e^{x_k}$ 로 나누는 방법이 이용된다.
$\frac {e^{x_i-x_k}} {e^{x_1-x_k} + ... + e^{x_n-x_k}}$ 가 되는데 임의의 j에 대하여 $x_j - x_k \leq 0 \quad and \quad 0 < e^{x_i-x_k} \leq 1$ 이 됨
즉 분모와 분자에 존재하는 모든 항이 0과 1 사이에 존재하고, $e^{x_k-x_k} = 1$ 이 분모에 항상 존재하기 때문에 분모는 항상 1보다 커져서 0으로 나누는 오류도 방지할 수 있다.

소프트맥수 함수의 편미분

백터를 입력받아 벡터를 출력하기 때문에 다대다 관계로 편미분 식이 매우 복잡함
어차피 역전파에서 진행할 편미분의 대상은 소프트맥스 함수가 아닌 소프트맥스 교차 엔트로피임
입력벡터(x_1,...,x_n)는 출력벡터 (y_1,...,y_n)에 영향을 미치므로 (x_j,y_j) 쌍에 대한 편미분 값들로 구성된 2차원 행렬을 구해야 함
모든 원소 쌍에 대한 편미분 $\frac {\partial y_j}{\partial x_j}$ 을 야코비안 행렬이라고 읽음
결론적으로는 야코비안 행렬을 미니배치 단위로 병렬 처리 하기 때문에 3차원 텐서로 볼 수 있음

$y_j = \frac {e^{x_j}} {e^{x_1} + ... + e^{x_n}}$

$\frac {\partial y_j}{\partial x_i} = - \frac {e^{x_j}(e^{x_1} + ... + e^{x_n})'} {(e^{x_1} + ... + e^{x_n})^2} = - \frac {e^{x_j}e^{x_i}} {(e^{x_1} + ... + e^{x_n})^2}$

$= - \frac {e^{x_i}} {(e^{x_1} + ... + e^{x_n})} \frac {e^{x_j}} {(e^{x_1} + ... + e^{x_n})} = -y_iy_j \quad (s.t \; i \neq j)$

$\frac {\partial y_i}{\partial x_i} = \frac {e^{x_j}(e^{x_1} + ... + e^{x_n})' - e^{x_i}e^{x_j}} {(e^{x_1} + ... + e^{x_n})^2} = \frac {e^{x_j}e^{x_i}} {(e^{x_1} + ... + e^{x_n})^2}$

$= \frac {e^{x_i}} {(e^{x_1} + ... + e^{x_n})} (1 - \frac {e^{x_i}} {(e^{x_1} + ... + e^{x_n})}) = y_i(1-y_i) = y_i - y_i^2 \quad (s.t \; i = j)$

소프트맥스 교차 엔트로피

H(P,Q) = -\sum_{i=1}^m p_i \log q_i

로짓 벡터 (a_1, ... ,a_n)의 분포를 Q, 정답 벡터 (y_i,...,y_n)을 Q로 삼아 교차 엔트로피 정의식에 적용
보통 정답 벡터는 0,1로 표현되는데, log 계산에 0이 들어가면 결과값이 -∞으로 나오기 때문에, 확률 분포 P로 삼는 것이 유리함
로짓 벡터는 소프트맥스 함수 덕분에 항상 0과 1 사이로 나오지만 유난히 작은 로짓값은 실수의 표현 범위 문제로 0으로 간주 되어 -∞ 계산 폭주 문제를 발생시킴
이에 대한 해결책으로 ε를 보정하여 사용 (하한선 역할을 해서 폭주를 막음)
$H(P,Q) = -\sum p_i \log q_i \approx -\sum p_i \log (q_i + \epsilon)$

소프트맥스 교차 엔트로피의 편미분

\frac {\partial H}{\partial x_i} = q_i -p_i

신경망이 추정한 로짓벡터 $x_1, ... ,x_n$ 정답 벡터 $p_1, ..., p_n$ 가 존재할 때 로짓 벡터로부터 소프트맥스 함수를 활용하여 추정한 확률 분포를 $q_1, ... ,q_n$ 을 두고 실행

$q_i = \frac {e^{x_i}} {e^{x_1} + ... + e^{x_n}}$

$H = -\sum_{i=1}^n p_i \log q_i$

$\frac {\partial H}{\partial x_i} = -\frac{\partial}{\partial x_i}\sum_{k=1}^n p_k \log q_k = -\sum_{k=1}^n \frac{\partial}{\partial x_i}p_k \log q_k$

$= -\sum_{k=1}^n p_k\frac{\partial}{\partial x_i}\log q_k =-\sum_{k=1}^n p_k\frac{1}{q_k}\frac{\partial q_k}{\partial x_i} \quad(by 연쇄법칙)$

마지막 식에서 $\frac{\partial q_k}{\partial x_i}$ 는 소프트맥스 함수의 편미분을 의미하고, 편미분 값은 $-q_iq_k \;\, (s.t \; i \neq k), \quad q_i - q_i^2 \; \, (s.t \; i = k)$ 로 조건에 따라 계산 식이 다름

$\frac {\partial H}{\partial x_i} = -\sum_{k=1}^n \frac {p_k}{q_k}\frac{\partial q_k}{\partial x_i} = -\sum_{k=i} \frac{p_k}{q_k} \frac{\partial q_k}{\partial x_i} -\sum_{k \neq i} \frac {p_k}{q_k}\frac{\partial q_k}{\partial x_i}$

$= -\frac{p_i}{q_i} \frac{\partial q_i}{\partial x_i} -\sum_{k \neq i} \frac {p_k}{q_k}\frac{\partial q_k}{\partial x_i} = -\frac{p_k(q_i -q_i^2)}{q_i} -\sum_{k \neq i} \frac {p_k(-q_iq_k)}{q_k}$

$=p_iq_i - p_i +\sum_{k \neq i}p_kq_i = \sum_{k=1}^np_kq_i - p_i = q_i \sum_{k=1}^np_k -p_i$
전체 확률 값의 합은 1 즉 $\sum_{k=1}^np_k =1$ 이고 따라서 $\frac {\partial H}{\partial x_i} = q_i - p_i$

시그모이드 함수와 소프트맥스 함수의 관계

시그모이드 함수는 두 후보 항목을 갖는 소프트맥스 함수에서 입력벡터 $exist \, x_1,x_2 ; \; x_2=0$ 로 설정해 입력 변수를 하나로 줄인 함수
소프트맥스 함수 대신 시그뫼드 함수를 선택 분류에 사용해도 큰 문제는 없음
후보 항목들의 로짓값에 소프트맥스 함수 대신 시그모이드 함수를 적용하면 각 항목이 답으로 선택될 확률이 구해지지만 그 합이 1로 맞취지진 않음 즉 개별 확률로 구해지고 그 중 가장 큰 확률을 선택하면 됨

구현코드 및 Annotation

선택 분류: 철판 불량 상태 분류 신경망

철판 표면 상태의 불량 여부, 불량 종류를 판별하는 신경망
단층 퍼셉트론
소프트맥스 함수와 소프트맥스 교차 엔트로피
Data : faulty-steel-plates Data (Kaggle)
- 1941개의 철판 재료(rows)
- 27가지의 특성(columns)
- 7가지 철판 불량 상태(target):one-hot-encoding하면 7개의 칼럼
성능은 좋지 않고 결과 또한 들쭉날쭉한데 이는 데이터 양이 적기 때문
27차원 벡터 공간을 7개 구역으로 적절하게 분할할 수 있어야 함
이에 대해 1941개의 불량 철판 데이터는 너무 적음
혹은 단층 퍼셉트론의 구조가 낮은 품질의 또다른 원인일수도 있음

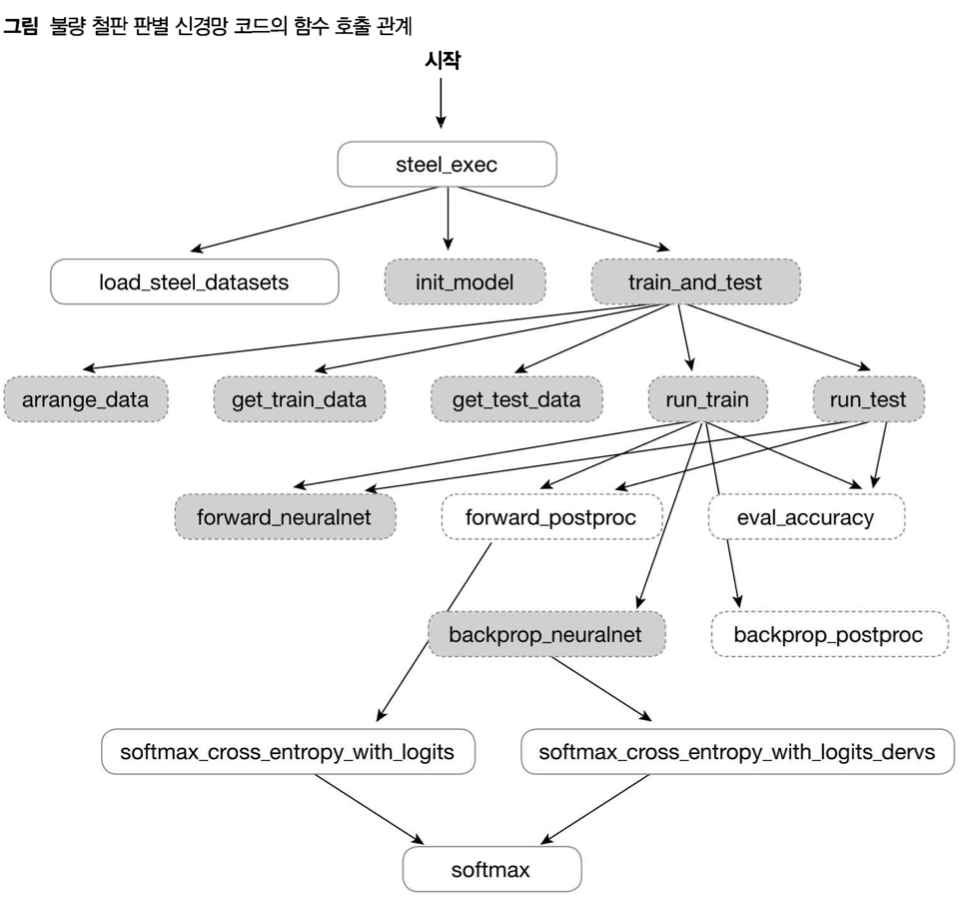
점선은 ch1에서 사용된 함수들을 그대로 사용한다는 의미 | 실선은 새롭게 선언

구현 코드 및 파일 실행

%run ../ch01/단층퍼셉트론(SLP).ipynb

메인 함수 정의

def steel_exec(epoch_count=10, mb_size=10, report=1):
    load_steel_dataset()
    init_model()
    train_and_test(epoch_count, mb_size, report)

데이터 적재 함수 정의

def load_steel_dataset():
    with open('/Users/andonghyeon/Desktop/Study/파이썬 날코딩으로 알고 짜는 딥러닝/data/faults.csv') as csvfile:
        csvreader = csv.reader(csvfile)
        next(csvreader, None)     # 첫행을 읽지 않고 건너뛴다
        rows = []
        for row in csvreader:
            rows.append(row)
            
    global data, input_cnt, output_cnt
    input_cnt, output_cnt = 27, 7     # 출력데이터가 7열로 설정(원핫벡터)
    data = np.asarray(rows, dtype='float32')

후처리 과정에 대한 순전파와 역전파 함수의 재정의
- 시그모이드 교차 엔트로피는 확률값 하나를 입력 삼아 엔트로피 값을 계산
- 소프트맥스 교차 엔트로피는 여러 확률값으로 구성된 확률 분포 하나로부터 엔트로피 값을 구함
- 미니배치 사이즈를 N이라고 했을 때 시그모이드 교차 엔트로피는 (N,1), 하지만 소프트맥스 교차 엔트로피는 (N,7)로부터 (N,1)형태로 얻어짐

def forward_postproc(output, y):
    # output은 로짓값
    # 로짓값 -> 소프트맥스 교차 엔트로피를 -> loss 연산
    entropy = softmax_cross_entropy_with_logits(y, output)
    loss = np.mean(entropy) 
    return loss, [y, output, entropy]

def backprop_postproc(G_loss, aux):
    y, output, entropy = aux
    #평균(loss) 역산(편미분)
    g_loss_entropy = 1.0 / np.prod(entropy.shape)
    #엔트로피 함수 역산(편미분)
    g_entropy_output = softmax_cross_entropy_with_logits_derv(y, output)
    
    G_entropy = g_loss_entropy * G_loss
    G_output = g_entropy_output * G_entropy
    #손실 기울기
    return G_output

정확도 함수 정의

def eval_accuracy(output, y):
    # np.argmax()는 각 로짓값을 담고 있는 최대값의 인덱스를 뽑아줌
    estimate = np.argmax(output, axis=1)
    answer = np.argmax(y, axis=1)
    # 둘 인덱스 간의 위치가 일치하면 True(1) 아니면 False(0)
    correct = np.equal(estimate, answer)
    
    return np.mean(correct)

소프트맥스 관련 함수 정의

def softmax(x):
    # 각 열에서 최대를 고르고(피쳐에 해당하는 최대)
    max_elem = np.max(x, axis=1)
    # 각 행을 전치시켜서 최댓값을 뺴주고 (행벡터 -> 열벡터)
    diff = (x.transpose() - max_elem).transpose()
    # 자연상수 처리 (열벡터)
    exp = np.exp(diff)
    # 자연상수 처리 한 것들을 합치고 (열벡터)
    sum_exp = np.sum(exp, axis=1)
    # 시그모이드 함수 수식 적용하고 전치 (열벡터 -> 행벡터)
    probs = (exp.transpose() / sum_exp).transpose()
    return probs

#실제로 호출되지 않지만 학습을 위한 구현
#소프트맥스 함수 자체보다 교차엔트로피 값을 중심으로 이루어지기 때문
def softmax_derv(x, y):
    mb_size, nom_size = x.shape
    derv = np.ndarray([mb_size, nom_size, nom_size])
    #3중 반복문을 통한 야코비안 행렬
    for n in range(mb_size):
        for i in range(nom_size):
            for j in range(nom_size):
                derv[n, i, j] = -y[n,i] * y[n,j]
            derv[n, i, i] += y[n,i]
    return derv

#log함수 폭주를 막기위해 epsilon 값을 10^(-10)값을 사용함
#labels는 원-핫 벡터
def softmax_cross_entropy_with_logits(labels, logits):
    probs = softmax(logits)
    return -np.sum(labels * np.log(probs+1.0e-10), axis=1)

def softmax_cross_entropy_with_logits_derv(labels, logits):
    return softmax(logits) - labels