다층퍼셉트론(MLP)

DonghyunAnn·2022년 1월 3일

딥러닝

파이썬 날코딩으로 알고 짜는 딥러닝

목록 보기

4/5

윤덕호 저서 파이썬 날코딩으로 알고 짜는 딥러닝을 공부하고 개인적으로 정리한 글입니다.
사진, 내용, 코드는 책을 참고한 것입니다. 코드는 오픈소스로 저저의 깃허브에 모두에게 공개되어있습니다.
Ch1 - 단층퍼셉트론(SLP), Ch2 - 단층퍼셉트론(Sigmoid-이진판단), Ch3 - 단층퍼셉트론(Softmax-선택분류)의 코드를 수정 및 재활용 했습니다.

다층 퍼셉트론 신경망 구조

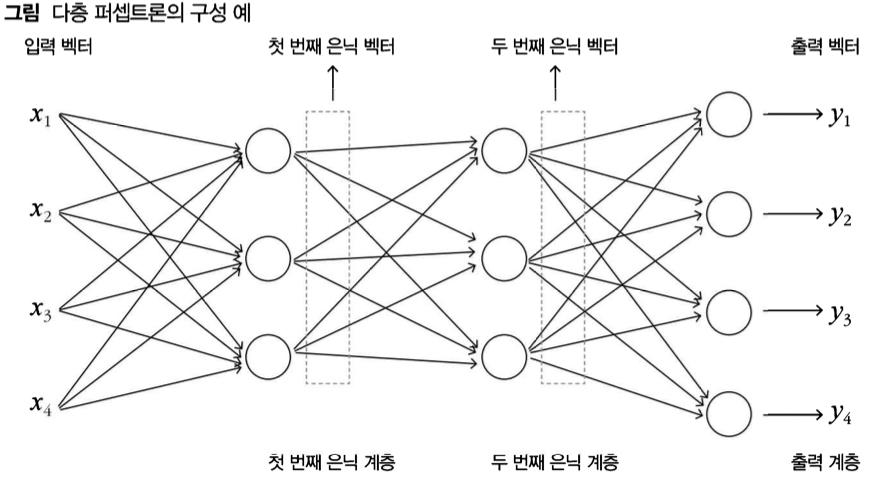
복수의 퍼셉트론 계층을 순서를 두고 배치하여, 중간 표현을 거쳐 출력 벡터를 얻어내는 신경망, 은닉 계층을 적어도 하나 이상 갖는 것이 보통
다층 퍼셉트론에서 각각의 계층은 단층 퍼셉트론과 같은 내부 구조
하나의 계층 내 퍼샙트론들은 동일한 입력을 공유하고 각각의 출력하고 인접한 계층끼리 앞 계층의 출력은 뒤 계층의 입력으로 제공됨, 인접 계층끼리는 완전 연결 방식
단층퍼셉트론은 0개의 은닉 계층을 갖는 다층 퍼셉트론의 특수한 경우라고 볼 수 있음

은닉 계층의 수와 폭

폭은 해당 계층이 갖는 퍼셉트론의 수이자 생성하는 은닉 벡터의 크기, 이 퍼셉트론을 노드라고 함
한 계층의 퍼셉트론들은 각각 해당 계층에 대한 입력 벡터 크기 만큼의 가중치와 편향 파라미터를 가짐
- 앞에 그림으로 제시된 신경망은 첫번째 은닉층 = 4 x 3 + 3 = 15, 두번째 은닉층 = 3 x 3 +3 = 12, 출력층은 3 x 4 + 4 = 16으로 총 43개의 파라미터를 갖음
은닉 계층을 추가해서 파라미터 수가 늘어나면 더 많은 학습 데이터가 필요해지는 경향이 있음
문제이 규모, 데이터양, 난이도를 종합적으로 고려해야 함, 따라서 은닉 계층 수와 폭 설정 값을 쉽게 바꾸어 실험할 수 있게 프로그램을 구현해야 함

비선형 활성화 함수

선형 연산 뒷단에 적용되어 퍼셉트론의 출력을 변형시키는 함수
일차 함수로 표현이 불가능한 좀 더 복잡한 기능을 수행 (ex) 시그모이드, 소프트맥스
출력 벡터를 구성하는 각 정보의 특성에 맞게 별도의 비선형 처리를 해야 하는데 출력 계층 안에 비선형 활성화 함수를 두면 코드가 지나치게 복잡해짐
출력 계층에는 비선형 활성화 함수가 사용되지 않는데 이 때문에 단층 퍼셉트론에서는 후처리 과정에서 비선형 함수를 사용하되 출력 계층 내부의 비선형 활성화 함수를 따로 다루지 않음
은닉 계층에서는 다음 은닉 계층, 출력 계층으로 입력하기 위해 비선형 함수가 사용됨
따라서 비선형 활성화 함수는 필수적 구성요소임, 선형 처리는 아무리 여러 단계를 반복해도 하나의 선형 처리로 줄여 표현할 수 있음(비선형 활성화가 없는 다층 퍼셉트론은 단층 퍼셉트론으로 만들 수 있음)
노드 수가 많은 단층 구조 신경망보다 노드 수가 적은 다층 구조 신경망 성능이 훨씬 우수한 경우가 많음 입력 데이터로부터 유용한 정보를 추출해내는 추상화에 다층구조가 더 효과적이기 때문, 딥러닝이 부각되계된 계기

ReLU 함수

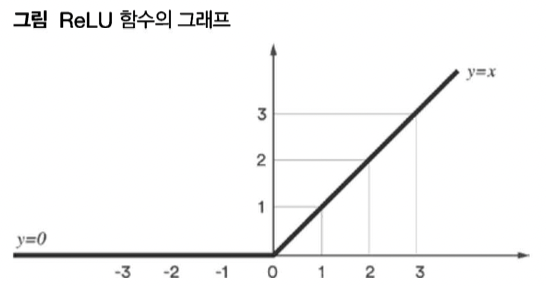
음수 입력을 걸러내 0으로 만드는 함수, 은닉 계층의 비선형 활성화 함수로 가장 많이 이용됨
시그모이드나 소프트맥스는 복잡한 계산과정 때문에 처리 부담이 크며, 소프트 맥스는 벡터 원소들을 묶어 처리하기 때문에 은닉 계층 출력 처리에는 부적합함
x = 0 에서 미분이 불가능한 것이 문제인데, 미분값을 0우로 강제 할당함, 별문제 없는 경우가 다수
이렇게 되면 미분 후 계산이 쉬워 지는데 양수이면 1로 음수이면 0 으로 출력됨 (numpy.sign(y) 사용 가능)

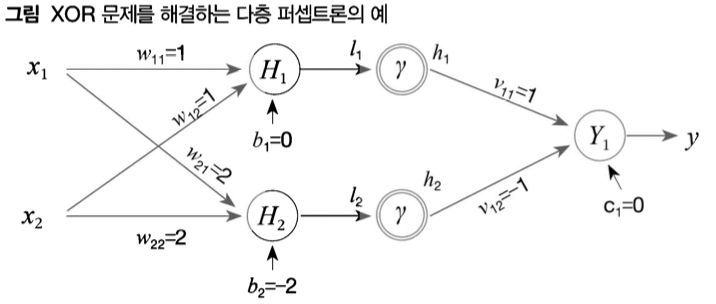
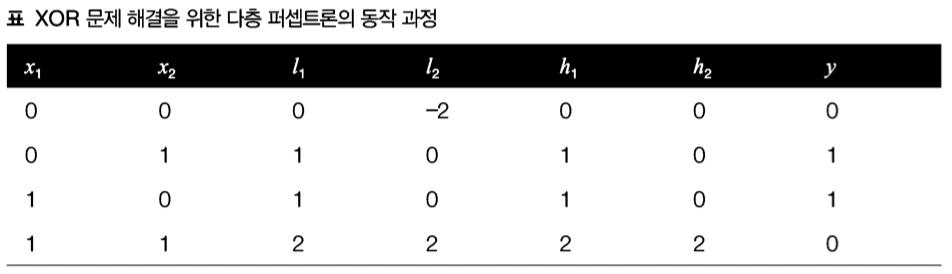
민스키의 XOR 문제와 비선형 활성화 함수

단층에서는 해결하지 못하는 문제

$y = f(x_1,x_2) = w_1x_1 +w_2x_2 + b$
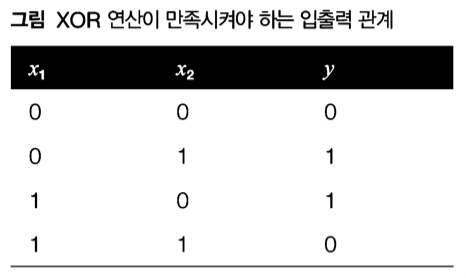
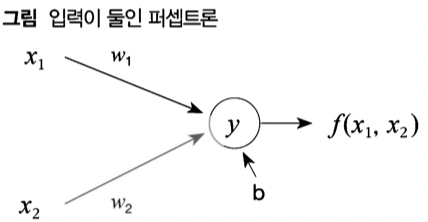
구조적으로 x와 y는 비례 관계에 있음, 여기서 영향을 미치는 파라미터는 w인데, w_1은 x_1 증감에 따른 y에 영향을 주지 x_2값에 따라 방향을 바꿀 수 는 없음, 따라서 단층에서는 해결할 수 없음 (민스키의 주장)

-이에 대한 해결책이 비선형 활성화 함수를 동반한 다층 퍼셉트론

구현코드 및 Annotation

앞선 설명에서 다뤘던 전복 고리 수 추정, 천체 펄서 판정, 철판 불량 유형 분류 문제를 다층 퍼셉트론 신경망으로 해결

수정이 필요한 함수

파라미터 초기화 함수 | 순전파 함수 | 역전파 함수
단층 퍼셉트론에 맞는 방법으로 정의된, 신경망 내부 처리에 직접적으로 관련된 함수

def init_model():
    global weight, bias, input_cnt, output_cnt
    weight = np.random.normal(RND_MEAN, RND_STD,[input_cnt, output_cnt])
    bias = np.zeros([output_cnt])

def forward_neuralnet(x):
    global weight, bias
    output = np.matmul(x, weight) + bias
    return output, x

def backprop_neuralnet(G_output, x):
    global weight, bias
    g_output_w = x.transpose()
    
    G_w = np.matmul(g_output_w, G_output)
    G_b = np.sum(G_output, axis=0)

    weight -= LEARNING_RATE * G_w
    bias -= LEARNING_RATE * G_b

은닉 계층 하나를 위한 파라미터 생성 함수 정의
- 단층 퍼셉트론에서 사용한 init_model() 함수와 비슷한 기능을 하지만 두 쌍의 파라미터를 저장하고 hidden_cnt라는 파라미터를 전달 받는 다는 점에서 다름

def init_model_hidden1():
    global pm_output, pm_hidden, input_cnt, output_cnt, hidden_cnt
    
    #은닉 계층 파라미터
    pm_hidden = alloc_param_pair([input_cnt, hidden_cnt])
    #출력 계층 파라미터
    pm_output = alloc_param_pair([hidden_cnt, output_cnt])
    
def alloc_param_pair(shape):
    #계층 하나를 위한 파라미터 쌍 생성
    weight = np.random.normal(RND_MEAN, RND_STD, shape)
    #2차원 형태를 넘는 것을 대비해 편향은 shape의 마지막 순서로 할당
    bias = np.zeros(shape[-1])
    return {'w':weight, 'b':bias}

은닉 계층 하나를 위한 순전파 함수 정의

def forward_neuralnet_hidden1(x):
    # init_model_hidden1 쌍의 파라미터에 접근
    global pm_output, pm_hidden
    
    #입력 x와 pm_hidden을 통해 은닉계층 출력 계산 Relu함수 사용
    hidden = relu(np.matmul(x, pm_hidden['w']) + pm_hidden['b'])
    #hidden과 pm_output을 통해 출력계층 출력이자 최종출력 output 계산
    output = np.matmul(hidden, pm_output['w']) + pm_output['b']
    
    #출력 계층의 역전파 처리 때 가중치에 대한 편미분 정보로 hidden이 필요함
    return output, [x, hidden]

def relu(x):
    return np.maximum(x, 0)

단층 퍼셉트론 vs 다층 퍼셉트론 역전파 편미분 차이

단층 퍼셉트론 알고리즘 구조 $X\rightarrow [F(x) = WX+B] \Rightarrow Y$ $Y\rightarrow [G(Y) = Loss function(Y)] \Rightarrow L$ -역전파를 진행할 때 편미분을 진행함 (기울기에 대한 미분) $\frac {\partial L} {\partial Y_{ij}} \frac{\partial Y_{ij}}{\partial W_{kj}} = G_{ij}X_{ik}$
이와 같이 단층 퍼셉트론은 역전파를 진행할 때 손실기울기를 위한 연산은 한 번으로 충분함 (기울기 수정을 한 차례만 진행하면 되기 때문)
다층 퍼셉트론 알고리즘 구조 $X \rightarrow [F_1(x) = W_1X+B_1] \Rightarrow Hidden\,Output = H_o$ $H_o \rightarrow [R(H_o) = ReLU(H_o)] \Rightarrow Hidden\,Input = H_i$ $H_i \rightarrow [F_2(H_i)= W_2H_i + B_2] \Rightarrow Y$ $Y \rightarrow [G(Y) = Loss function(Y)] \Rightarrow L$
단층 퍼셉트론에선 (X -> Y -> L) 다층 퍼셉트론에서는 (X -> Hidden output -> Hidden input -> Y -> L)로 순전파 처리가 됨
- 다층 퍼셉트론은 (Hidden input -> Y -> L), (X -> Hidden output -> Hidden input -> Y) 두 단계에서 손실 기울기를 구해야 함
- ReLU함수는 기울기 수정을 할 필요가 없기 때문에 두번의 기울기에 대한 미분을 구하면 됨
  $\frac {\partial L} {\partial Y} \frac{\partial Y}{\partial W_2} = GH_i$ $\frac {\partial Y} {\partial H_i}\frac {\partial H_i} {\partial H_o} \frac{\partial H_o}{\partial W_1} = W_2 R'(H_o)X \quad (s.t \; R'(H_o) = H_i')$

은닉 계층 하나를 위한 역전파 함수 정의
- 단층 퍼셉트론에서 구현한 backprop_neuralnet()의 처리를 출력 계층과 은닉 계층에 대해 반복함
- 두 계층 처리 사이에 역전파를 위한 G_hidden부분이 추가됨

def backprop_neuralnet_hidden1(G_output, aux):
    # G_output은 역전파 후처리 후만들어지는 파라미터
    global pm_output, pm_hidden
    
    # 순전파에 사용됐던 input
    x, hidden = aux
    
    # 출력층에 대한 역전파
    # 출력층에서 사용하는 input은 hidden 
    g_output_w_out = hidden.transpose()                      
    G_w_out = np.matmul(g_output_w_out, G_output)            
    G_b_out = np.sum(G_output, axis=0)    
    
    # 출력 계층과 은닉 계층 역전파 처리 매개하는 G_output으로부터 G_hidden을 구해내는 과정
    g_output_hidden = pm_output['w'].transpose()
    # pm_output['w']은 변환이 되는 계수이기 때문에 미리 기록한 것 위에 명시된 식에서 W_2
    G_hidden = np.matmul(G_output, g_output_hidden)   
    
    # 출력층 역전파
    pm_output['w'] -= LEARNING_RATE * G_w_out                
    pm_output['b'] -= LEARNING_RATE * G_b_out                
    
    # 은닉층 -> relu -> 출력층 순서
    # 역전파는 그 반대로 가야하기 때문에 Relu 부분을 처리해줘야 함 위 식에서 편미분값
    G_hidden = G_hidden * relu_derv(hidden)
    
    # 은닉층에 대한 역전파
    # 은닉층에서 사용하는 input은 x
    g_hidden_w_hid = x.transpose()
    G_w_hid = np.matmul(g_hidden_w_hid, G_hidden)            
    G_b_hid = np.sum(G_hidden, axis=0)                       
    
    # 은닉층 역전파
    pm_hidden['w'] -= LEARNING_RATE * G_w_hid                
    pm_hidden['b'] -= LEARNING_RATE * G_b_hid                
    
def relu_derv(y):
    return np.sign(y)

가변적 은닉 계층 구성을 위한 파라미터 생성 함수 정의

def init_model_hiddens():
    # 은닉 계층의 수와 폭은 hidden_config리스트를 통해 지정
    global pm_output, pm_hiddens, input_cnt, output_cnt, hidden_config
    
    pm_hiddens = []
    prev_cnt = input_cnt
    
    # 리스트 성분 개수 = 계층의 수 | 리스트 성분 = 폭
    # 반복문을 통해 prev_cnt를 갱신해서 은닉층의 벡터 크기를 맞물리게 갱신
    for hidden_cnt in hidden_config:
        pm_hiddens.append(alloc_param_pair([prev_cnt, hidden_cnt]))
        prev_cnt = hidden_cnt
    
    #은닉층은 반복문이었지만 출력층은 하나이기 때문에 먼저 제시한 1개짜리 함수와 동일 
    pm_output = alloc_param_pair([prev_cnt, output_cnt])

가변적 은닉 계층 구성을 위한 순전파 함수 정의
- foward_neuralnet_hidden1 함수 를 은닉 계층 수만큼 반복해주면 됨

def forward_neuralnet_hiddens(x):
    # pm_hiddens는 앞에서 생성한 파라미터들
    global pm_output, pm_hiddens
    
    # 처음에 x로 input되어 첫번째 은닉층의 입력으로 이용됨
    hidden = x
    # input들이 정리된 리스트
    hiddens = [x]
    
    for pm_hidden in pm_hiddens:
        # hidden이 다음 층의 입력으로 초기화 됨
        hidden = relu(np.matmul(hidden, pm_hidden['w']) + pm_hidden['b'])
        hiddens.append(hidden)

    # 마지막에는 출력층의 입력으로 초기화
    output = np.matmul(hidden, pm_output['w']) + pm_output['b']
    
    # 출력층의 결과, 은닉층의 결과 리스트는 보조 정보로 활용
    return output, hiddens

가변적 은닉 계층 구성을 위한 역전파 함수 정의

def backprop_neuralnet_hiddens(G_output, aux):
    global pm_output, pm_hiddens
    
    #foward_neuralnet_hiddens에서 파생된 hiddens가 aux로 input됨
    hiddens = aux
    
    # 출력층에서부터 역전파 시작 [-1]은 마지막 층을 출력을 가져오기 위해
    g_output_w_out = hiddens[-1].transpose()
    G_w_out = np.matmul(g_output_w_out, G_output)
    G_b_out = np.sum(G_output, axis=0)
    
    # 기울기 수정 전 Relu역전파를 위한 기울기 저장
    g_output_hidden = pm_output['w'].transpose() 
    G_hidden = np.matmul(G_output, g_output_hidden)
    
    # 출력층 기울기 수정
    pm_output['w'] -= LEARNING_RATE * G_w_out
    pm_output['b'] -= LEARNING_RATE * G_b_out
    
    # 반복문을 통해 은닉층 역전파, reversed()를 통해 뒤에서부터 가져옴
    # hiddens의 길이가 아닌 pm_hiddens의 길이를 반영
    # 처리해야하는 횟수는 은닉층의 개수 만큼 (pm_hiddens)이기 때문
    for n in reversed(range(len(pm_hiddens))):
        # Relu의 역전파 처리 부분
        # 입력벡터 pm_hiddens[n]를 relu함수의 역전파 처리를 위해 필요한 출력 벡터 내용에는 hiddens[n+1]로 접근
        G_hidden = G_hidden * relu_derv(hiddens[n+1])

        g_hidden_w_hid = hiddens[n].transpose()
        G_w_hid = np.matmul(g_hidden_w_hid, G_hidden)
        G_b_hid = np.sum(G_hidden, axis=0)
    
        g_hidden_hidden = pm_hiddens[n]['w'].transpose()
        G_hidden = np.matmul(G_hidden, g_hidden_hidden)

        pm_hiddens[n]['w'] -= LEARNING_RATE * G_w_hid
        pm_hiddens[n]['b'] -= LEARNING_RATE * G_b_hid

스위치 함수 정의
- 전역 변수 성정에 따라 두 부류 함수를 선택적으로 호출할 수 있음

global hidden_config

def init_model():
    # 값이 설정되어 있으면 
    if hidden_config is not None:
        print('은닉 계층 {}개를 갖는 다층 퍼셉트론이 작동되었습니다.'. \
              format(len(hidden_config)))
        init_model_hiddens()
        
    # 설정 되어있지 않으면
    else:
        print('은닉 계층 하나를 갖는 다층 퍼셉트론이 작동되었습니다.')
        init_model_hidden1()

# 신경망 순전파
def forward_neuralnet(x):
    if hidden_config is not None:
        return forward_neuralnet_hiddens(x)
    else:
        return forward_neuralnet_hidden1(x)

#신경망 역전파
def backprop_neuralnet(G_output, hiddens):
    if hidden_config is not None:
        backprop_neuralnet_hiddens(G_output, hiddens)
    else:
        backprop_neuralnet_hidden1(G_output, hiddens)

은닉 계층 구조 지정 함수 정의
- hidden_config는 list 형식 | hidden_cnt는 int 형식

def set_hidden(info):
    global hidden_cnt, hidden_config
    if isinstance(info, int):
        hidden_cnt = info
        hidden_config = None
    else:
        hidden_config = info