올바른 괄호 문자열

Baekjoon 3012

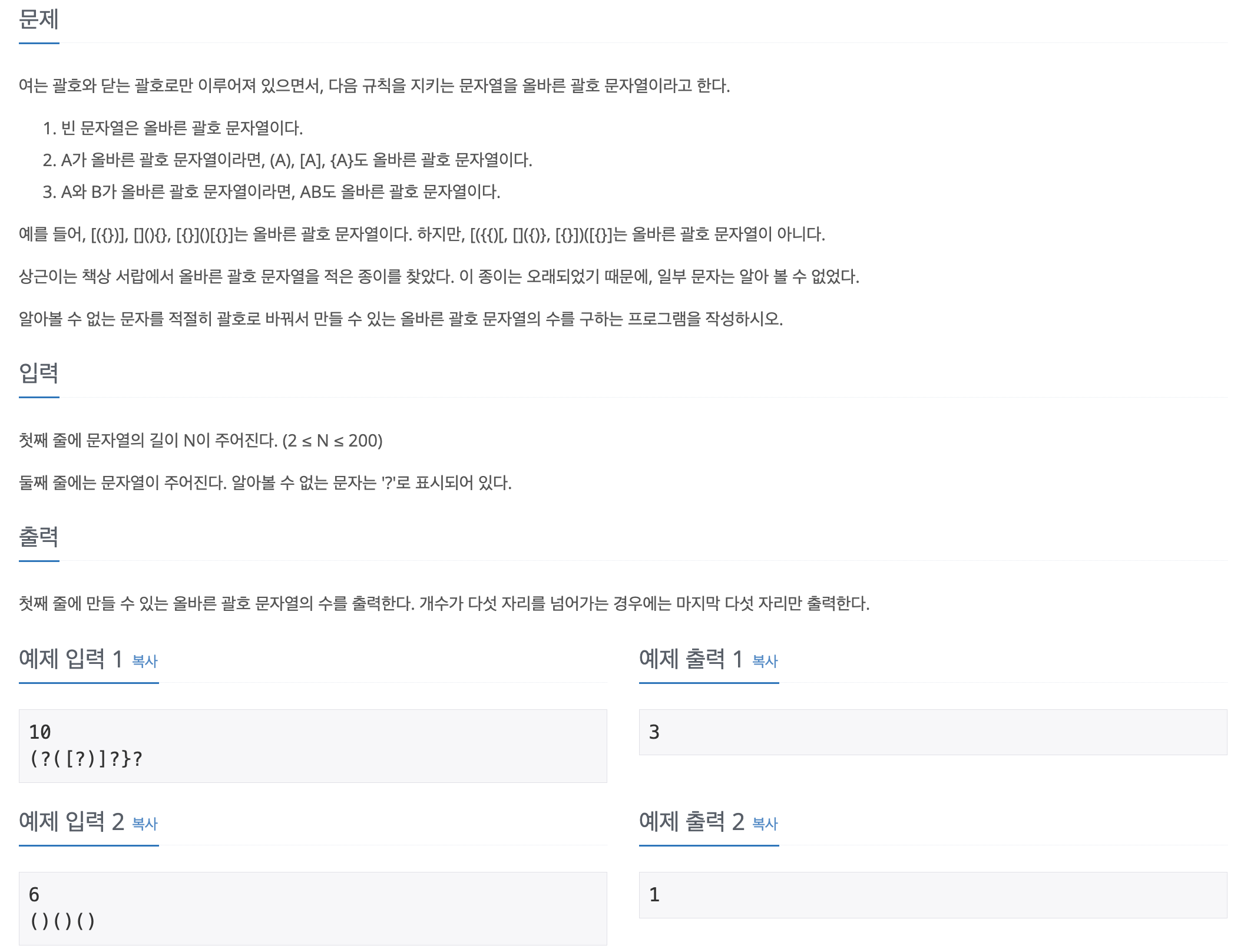
Problem

Solution

This problem uses range dp (dp[i][j]), which I am not familiar of yet... Once you figure out that it can be solved using range dp, the dp equation itself it pretty easy to derive.

$dp[i][j]=\sum dp[i][k] \cdot dp[k+1][j]$

Beware of handling question marks, and the output condition is pretty annoying (have to use %05lld)

Code

#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
const long long MOD=100000;
long long N, dp[210][210];
string s, open="([{", close=")]}";
long long solve(long long start, long long end){
    long long &r=dp[start][end];
    if(start>end) r=1;
    if(r!=-1) return r;
    else{
        r=0;
        for(long long i=start+1; i<=end; i+=2){
            for(long long j=0; j<3; j++){
                if(s[start]==open[j] || s[start]=='?'){
                    if(s[i]==close[j] || s[i]=='?'){
                        r+=solve(start+1, i-1)*solve(i+1, end);
                        if(r>=MOD)
                            r=MOD+r%MOD;
                    }
                }
            }
        }
    }
    return r;
}
int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> N;
    cin >> s;
    fill(&dp[0][0], &dp[209][210], -1);
    long long temp=solve(0, (long long)s.length()-1);
    if(temp>=MOD)
        printf("%05lld\n", temp%MOD);
    else cout << temp << "\n";
    return 0;
}