1. 데이터로 도수분포표 만들기

• 정규분포의 첫걸음은 히스토그램 만들기
• 대략적인 순서는
  1. 데이터 : 공공기관 데이터, 회사 등의 매출 데이터
  2. 도수분포표 : 원시 데이터를 이용하여 최댓값,최솟값(범위) / 그래프 폭(계급)과 빈도 등을 통해 도수분포표 완성
  3. 히스토그램 : 도수분포표를 이용하여 히스토그램 생성, 분포상황을 한눈에 파악
• 데이터의 구간을 나눔 이를 계급이라 함
• 적정한 계급 수(구간 수)를 구하는 기준은 스터지스의 법칙
• 스터지스의 법칙 : 표본이 수를 n이라 했을 때 계급 수 K를 구하는 공식은 $K = log_{2}n$ 임
• 계급값 : 해당 계급의 한가운데 값
• ex) 57.0~59.0 구간에 30개의 데이터가 있다고 한다면 이 계급의 계급값은 58.0, 해당 구간의 데이터를 모두 더하지 않아도 계급값을 통해 30 x 58.0 = 1,740과 같이 대략적인 값을 구할 수 있음

2. 히스토그램에서 쌍봉형을 발견했다면?

• 산(봉)이 2개인 쌍봉형 패턴은 데이터를 재확인 필요
  
• 단봉형이 2개 겹친 것이라면 이치에 맞지만,
• 서로 다른 데이터의 종류가 섞인 경우가 존재함
• ex) 여자의 키와 남자의 키가 섞인 경우

3. 히스토그램에서 분포곡선으로

• 키의 분포 등이라면 좌우 대칭을 이루는 깔끔한 종형 모양의 분포에 가까워질 것, 이를 정규분포라고 함
  
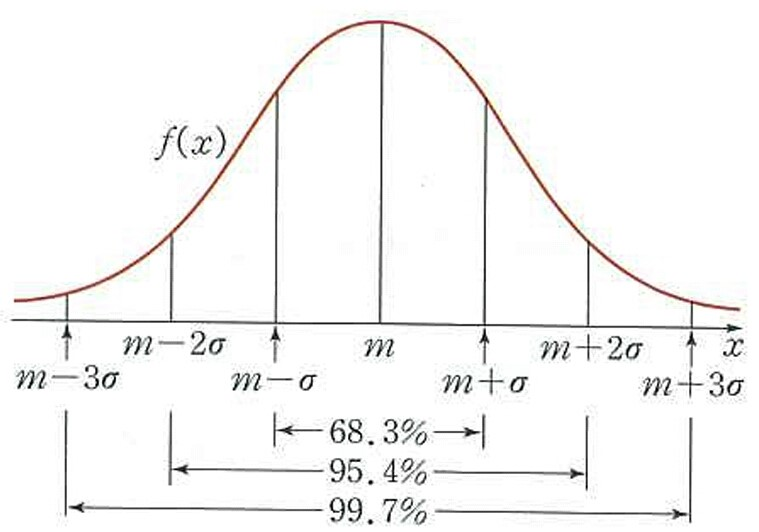
• 정규분포는 평균과 분산(표준편차)로 정해짐
• 정규분포에서는 '평균에서 얼마나 떨어져 있나?'로 해당 범위에 포함되는 데이터의 비율(확률)이 정해짐
• 그리고 그 거리 단위로 표준편차를 사용
• 100개의 데이터로 이루어진 정규분포에선 평균에서 $\pm1\sigma$ 거리에 68개 정도의 데이터가 포함됨

4. 정규분포 움직이기 ①: 평균 변경

• 평균이 달라지면 중심축이 달라짐
• 즉, 평균이 변하면 정규분포는 좌우로 움직이는 것
• 평균 = 0, 표준편차 = 1인 정규분포를 표준정규분포라고 함

5. 정규분포 움직이기 ②: 표준편차 변경

• 평균이 다르면 좌우 위치가 바뀌지만 표준편차가 다르면 형태가 달라짐
  

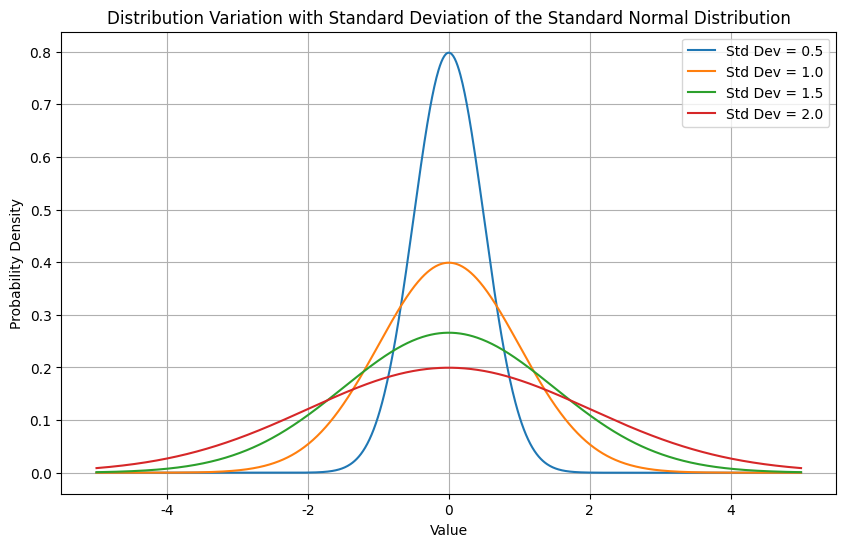
6. 정규분포로 확률 보기

• 정규분포곡선에서 '평균+표준편차(혹은 분산)'까지의 범위는 특정 데이터가 해당 범위에 포함될 확률을 나타냄
• $\pm1\sigma$ 위치는 수학에서 '변곡점'으로 불리는 위치, 곡선 위에서 가장 '기울기가 큰' 지점으로 이 지점을 기준으로 양쪽의 기울기가 작아짐
• 95% = 1.96시그마 / 99% = 2.58시그마

7. '관리도'를 이용한 품질관리

8. 2개의 서로 다른 정규분포를 1개로?

• 정규분포곡선을 사용하여 그대로는 비교하기 어려운 서로 다른 2개 데이터를 상대적으로 비교할 수 있음
• 예시를 들면,
  1. 고교생 홍길동 군이 전국모의고사에서 수학 73점, 영어 76점 획득
  2. 평균점수는 수학이 60점, 영어가 68점
  3. 표준편차는 수학이 8점, 영어가 6점
• 어느 과목의 성적이 우수할까?
  
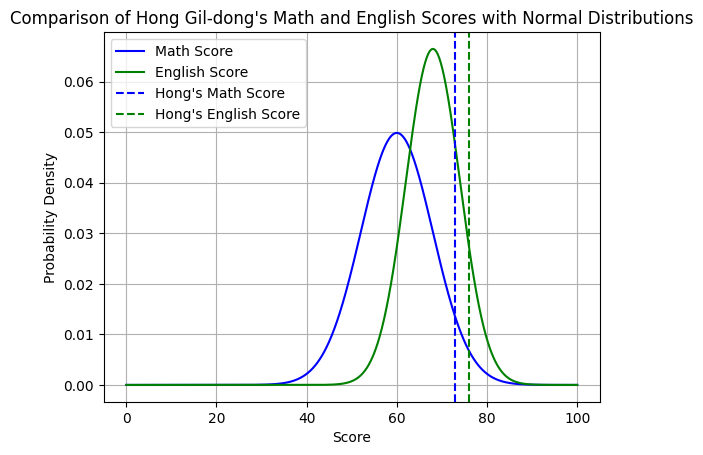
• 2개의 그래프를 (한데 모아) 같은 모양으로 만들면 비교가능

9. 여러 곳에서 사용할 수 있는 표준정규분포

표준점수, 표준화로 '비교할 수 있는 장소' 만들기

• 수학 : 점수 - 평균점수 = 73 - 60 = 13점
• 영어 : 점수 - 평균점수 = 76 - 68 = 8점
• 이 점수 차를 산포도(표준편차)와 대응시키려면 다음과 같이 생각할 수 있음
• '수학의 13점은 표준편차 8점에 대해 13/8 = 1.625에 해당'
• '영어의 8점은 표준편차 6점에 대해 8/6 = 1.333에 해당'
• 여기서 1.625나 1.333을 표준점수standard score 또는 표준화점수라고 함
• 원래 데이터에서는 수치가 모두 다르므로 비교하기 어렵지만,
• 표준점수를 계산함으로써, '표준편차를 1로 했을 때, 홍길동 군의 수학 및 영어 성적은 각각 1.625, 1.333'으로 그 차이를 수치로 비교할 수 있음
• 즉, '평균과의 차이'를 해당 과목의 표준편차로 나누면 표준점수를 계산할 수 있음
• 이는 전원의 성적을 '표준점수=1'에 대한 비율로 공통화한 것으로 표준화라고 함

표준정규분포는 평균=0, 표준편차=1

• 각자의 성적에서 표준점수를 계산하여 표준화했을 때 이를 나타내는 분포는 '평균 = 0, 표준편차 = 1인 정규분포'가 됨
• 무수히 많은 정규분포 중에서도 이러한 특별한 정규분포를 표준정규분포라 부름

개인의 위치 알기

• 수학의 표준점수 : 1.625 / 영어의 표준점수 : 1.333
• 이는 표준정규분포에서 표준편차1의 1.625배, 1.333배의 위치라는 것
• 표준정규분포표를 통해 %를 알 수 있음