1. 표본을 이용하여 모집단의 특징 추정

• 추측통계학을 이루는 두 기둥 "추정"과 "가설검정"
• 무엇을 추정하냐? 모집단의 평균, 분산, 비율(시청률과 비슷함)
• 추정의 순서는 "모집단의 평균을 추정하는 방법"만 알면 모두 비슷함
• 정규분포, $t$분포, $\chi^2$분포 사용함.
• 중심극한정리 : 모집단의 평균을 추정하는 추측통계학의 근거가 되는 중요한 정리

2. 통계학 용어정리

• 모평균($\mu$), 모분산($\sigma^2$), 모표준편차($\sigma$)
• 위의 모집단의 값들은 "통계량"이라 부르지 않음
• 일반적으로 평균, 분산, 표준편차는 모집단의 값들을 의미
• 표본평균($\overline{X}, \overline{x}$), 표본분산($s^2$), 표본표준편차($s, u$), 불편분산($u^2$)
• 위의 표본들의 값들은 "통계량"이라 부름
• 불편분산 : "분산"과 다르게 (데이터의 개수 - 1)로 나눔, "표본분산"은 (데이터의 개수)로 나눔
• 왜 불편분산 필요함?(왜 (데이터의 개수 - 1)로 나눔?)
  - 우리의 목적은 표본평균, 표본분산을 아는 것이 아니라 결과적으로 모집단의 평균과 분산을 추정하는 것
  - "표본분산"을 통해 모분산을 추정하면 모분산보다 작음
  - "불편분산"을 통해 모분산을 추정하면 모분산과 같음
• 이런 의미에서 "표본평균"과 "불편분산"은 "추정값"이 되지만,
• 표본분산은 모집단의 값을 정확히 추정할 수 없으므로 "추정값"이 될 수 없음

3. "점 추정"은 맞을 수도 틀릴 수도 있다?

• 표본의 평균이 그대로 모집단의 평균일 것 이다 => "점 추정"
• 점 추정과 달리 일정한 폭과 구간을 추정하는 방법 => "구간 추정"
• "구간 추정"을 위해 중심극한정리가 필요

4. "평균값의 평균"분포와 중심극한정리

• $\overline{X}$ = $\mu$의 경우, 즉 "점 추정"의 경우는 매우 찾아보기 힘듦
• 과수원에서 10개씩의 사과를 추출해 그 표본의 평균을 측정하면 매번 다를 것
• 아마 $\overline{X}$의 분포는 "정규분포"를 따를 것
• "표본평균($\overline{X}$)의 분포"의 특징은 다음과 같음

1. "표본평균($\overline{X}$)의 분포"의 평균은 모집단의 평균($\mu$)와 일치
2. "표본평균($\overline{X}$)의 분포"의 분산은 $\frac{\sigma^2}{n}$ (표준편차는 $\frac{\sigma}{\sqrt{n}}$) ($\mu$는 모집단의 표준편차)
3. 모집단의 분포가 어떠하든 표본 수n이 커질수록 "표본평균($\overline{X}$)의 분포"는 "정규분포"에 가까워짐

• 위 3가지 내용이 바로 중심극한정리
  

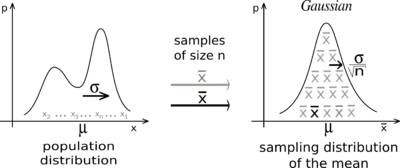
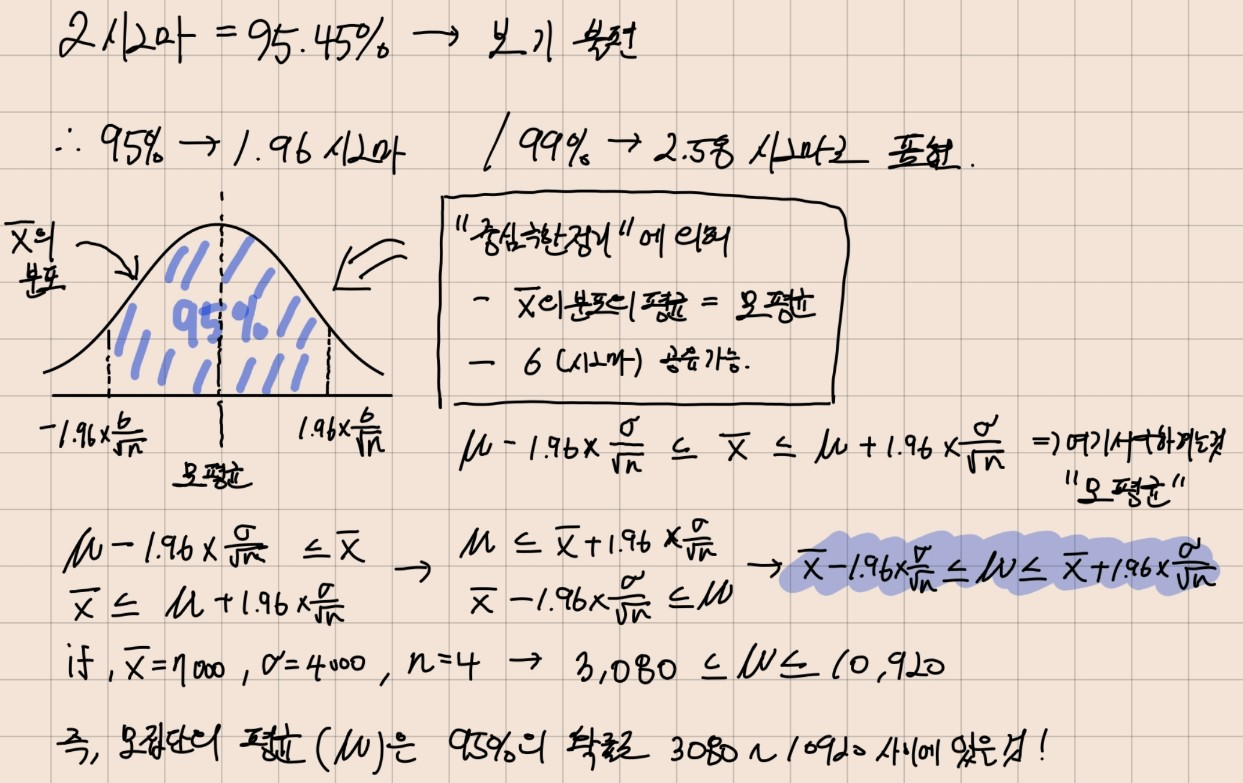
5. 구간으로 나타내는 "구간추정"

• "점 추정" : 표본평균이 모평균이다!
• "구간 추정" : 95%의 확률로 모평균이 5,500원 ~ 8,000원 사이에 있을 것이다!
• 즉, 일정확률과 구간으로 추정하는 것이 구간 추정
• 구간 추정에서는 중심극한정리 3번을 이용,
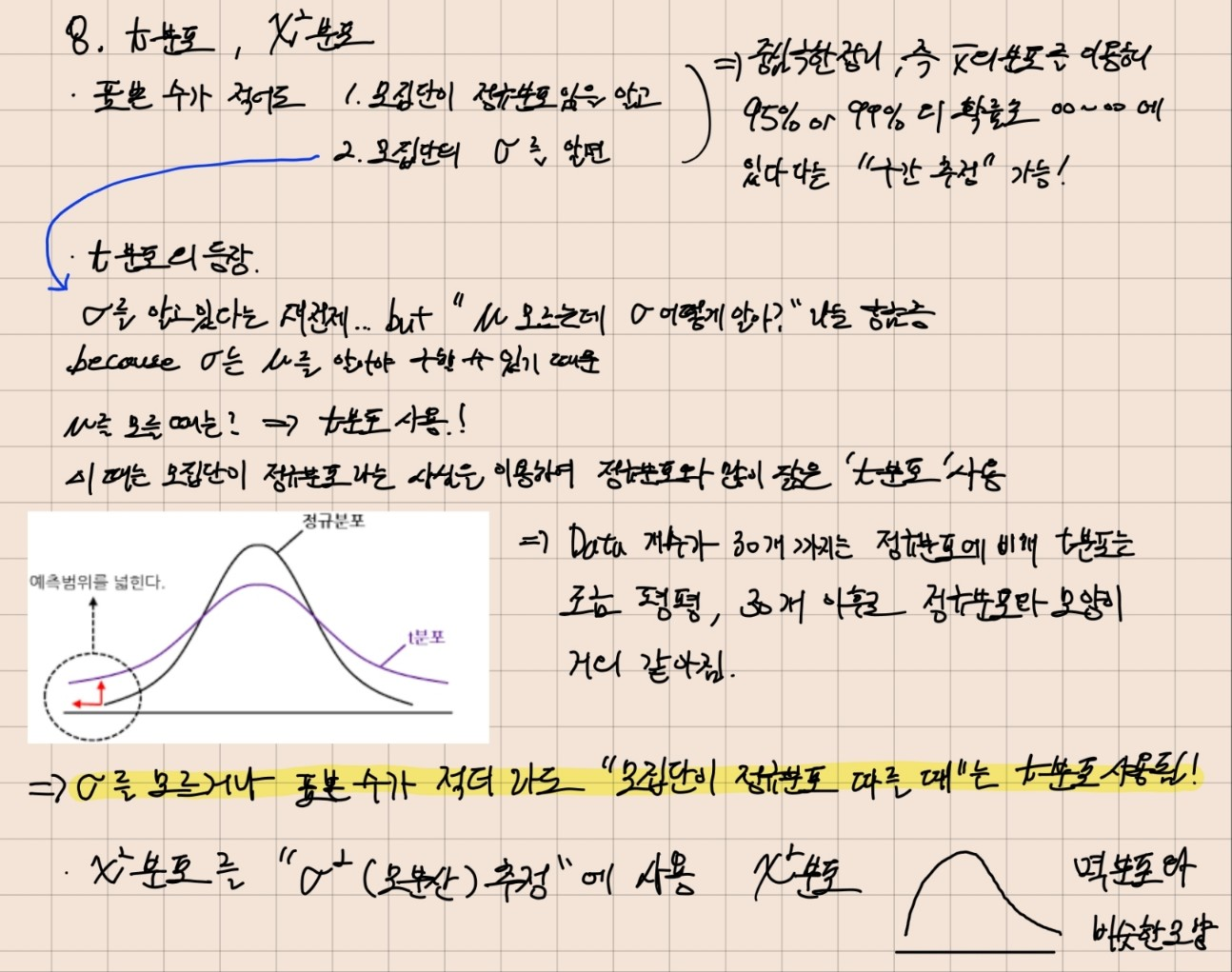
• 모집단의 분포가 어떠하든 표본 수n이 커질수록 "표본평균($\overline{X}$)의 분포"는 "정규분포"에 가까워짐 -> 이 말인 즉, 모집단이 "정규분포"임을 알고있다면 표본 수는 상관없다 (즉, 표본 수가 적어도 된다)
  

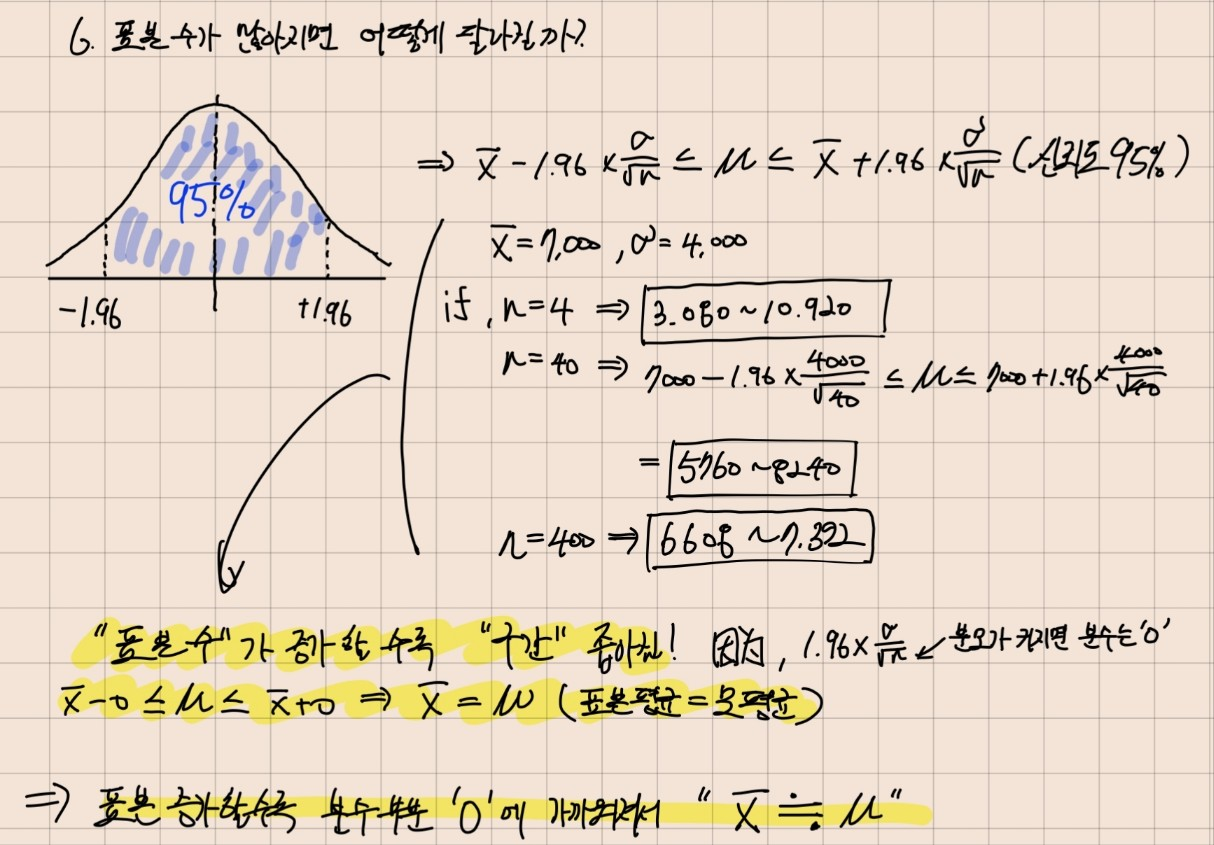
6. 표본 수가 많아지면 어떻게 달라질까?

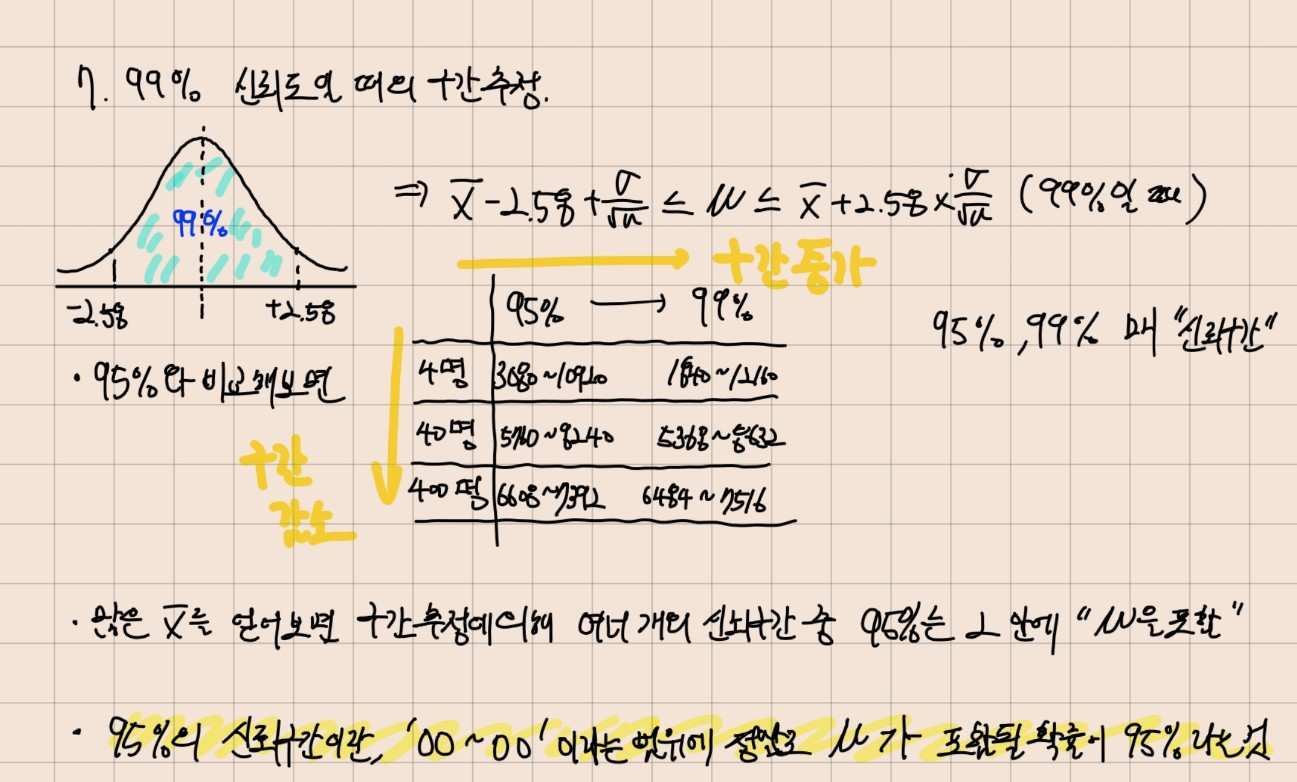
7. 99% 신뢰도 일 때의, 구간 추정

8. $t$분포, $\chi^2$분포

9. 시청률(모비율)은 어떻게 추정할까?

10. 설문조사 응답 수는 얼마가 적당할까?

• 설문조사 시 가장 신경쓰이는 것 : "응답 수에 따른 신뢰도는 어느정도 될까?"

• 이를 위해선 시청률의 "표본오차" 사용

• ex) X국가에 1,000만 가구가 있고 1,000가구 대상으로 시청률 조사 / Y국가는 6,000만 가구가 있고, 1,200가구 대상으로 시청률 조사 / 어느쪽이 오차가 더 작을까?

• 감각적으로 X는 1만 가구 당 1가구 / Y는 5만 가구 당 1가구 이므로 X가 더 작아보이지만 실제로 계산하면 Y국가의 오차가 더 작음

$-1.96\times\sqrt{\frac{p(1-p)}{n}}\le표본오차\le1.96\times\sqrt{\frac{p(1-p)}{n}}$

• 위 식을 살펴보면 n(조사한 가구 수)와 p(시청률)만 변함

• 즉, 뉴질랜드 133만 가구, 일본 5100만 가구, 중국 2억 7000만 가구와 같은 모집단의 개수와 상관없이 오차는 "조사한 가구 수"(표본 수)의 크기에 따라 결정

• 표본이 크면 오차가 작아짐