GAN은 GAN 관련 유튜브 강의
의 내용을 포함하여 이 글에서 GAN에 대해서 자세히 다루도록 하겠다.
Gernerative Model
그저 단순히 무언가를 생성하는 것만이 아닌 많은 것을 포함하는 개념
강아지의 이미지들이 주어졌다고 가정했을 때, 확률 분포 에 대하여 아래와 같은 것을 학습하는 것이 목표이다.
- Generation
~ 로 sampling했을 때, 강아지같아 보여야한다. - Density Estimation
x가 충분히 강아지같다면, p(x)가 충분히 높아야한다.
- Explicit Model이라고도 한다.
- 입력값에 대한 확률값을 얻을 수 있는 모델
- Unsupervised representation learning
강아지가 꼬리, 귀, 등의 특징이 있다고 생각한다.(Feature Learning)
그렇다면, 를 어떻게 구해야할까?
우리는 이산 확률 분포에서, Bernoulli와 Categorical이 있다는 사실을 알고 있다. 이를 바탕으로 RGB벡터에 대한 Joint Distribution을 구해보자.
~
위의 경우, 하나의 RGB픽셀에 대해서 상당히 많은 수의 파라미터가 필요하다는 것을 알 수 있다.
그렇다면 Binary Pixel이라고 생각해본다면, 전체 데이터가 n개라고 가정할 때, 우리는 parameter의 수를 이라고 생각할 수 있다.
대부분의 딥러닝이 그렇지만, 이렇게 파라미터의 수가 너무 커지는 것은 문제를 일으킬 가능성이 높아 이를 줄일 수 있는 방법이 필요하다.
그래서 n개의 픽셀들이 모두 independent하다고 생각해보자. 가능한 possible state는 이지만 모두 독립적이기 때문에 필요한 parameter수는 n개이다.(Very Strong Assumption) 그러나 이 방법은 너무 모델의 표현력이 떨어진다.
Important Three Rules
Chain rule:
Bayes' rule:
Conditional independence:
아무런 가정 없이, Joint Distribution을 Chain Rule을 활용한 곱으로 표현하면 다음과 같다.
아무런 가정이 없기 때문에 Fully Dependent모델과 같은 파라미터 수를 가질 것이다. ( 개)
그렇다면 여러가지 조건을 줘서 Fully Independent 모델과 Fully Dependent 모델 사이의 파라미터 개수를 가진 모델을 구할 수 있을 것이다.
Conditional Independence
(Markov assumption)라 가정하자. i+1번째 데이터는 i번째의 데이터에만 Dependent하고 나머지 정보에 대해서는 독립적이다. 그렇다면,
즉 총 파라미터의 수는
이다.
Hence, by leveraging the Markov assumption, we get exponential reduction on the number of parameters.
Auto-regressive models leverage this conditional independency.
Auto Regressive Model
기본적인 Auto Regressive Model은 현재 정보가 이전 정보에 Dependent한 Joint Distribution using Chain Rule 이다.(Markov 가정이 있든, 아무런 가정이 없든)
따라서, 우리는 Ordering이 필요하다. 순서를 매기는 방법이나 Conditional Independence 정보에 따라서 방법론이 달라질 수 있다.
NADE
i번째 픽셀을 1:i-1픽셀에 Dependent하게 하는 형식
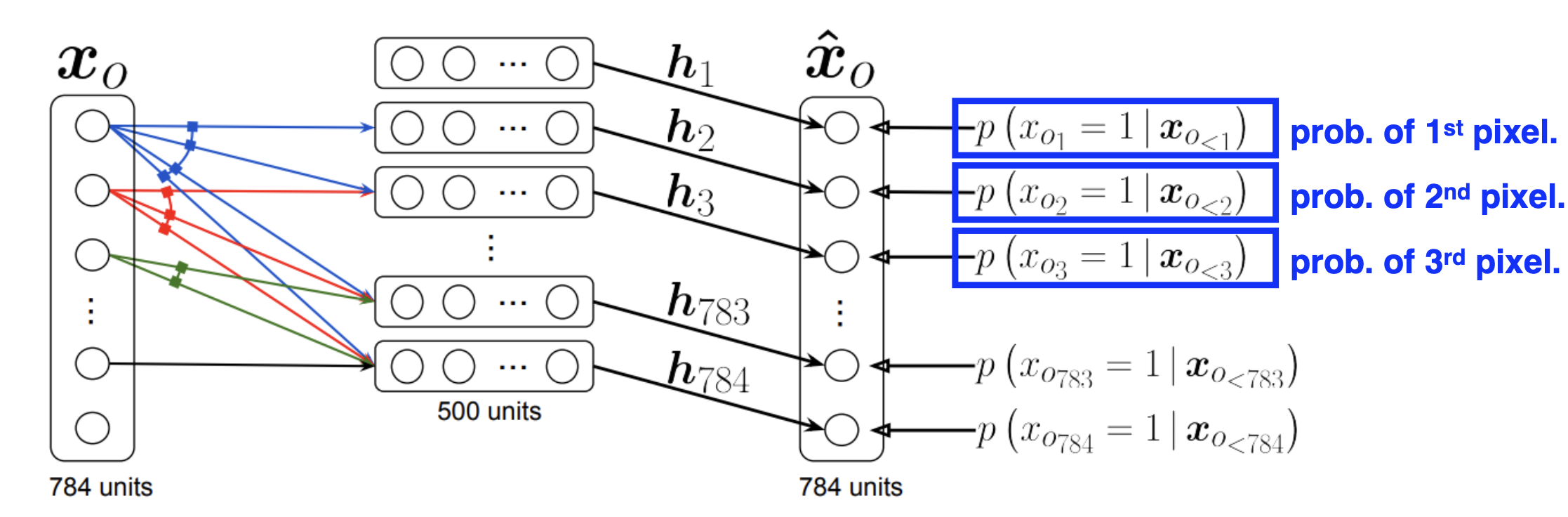
where
NADE is an explicit model that can compute the density of the given inputs.
Density를 구한다는 것 :
- 확률 분포를 구한다
- Explicit 모델이다
Suppose we have a binary image with 784 binary pixels, . Then, the joint probability is computed by
where each conditional probability is computed
independently.
In case of modeling continuous random variables, a mixture of Gaussian can be used.
Pixel RNN
- Row LSTM
- Diagonal BiLSTM
Latent Gradient Models
Autoencoder는 Generative model인가?
Variational Auto-Encoder
- Variational Inference(VI)
- 목적은 Variational Distribution이 Posterior Distribution과 가장 잘 Match하도록 Optimize하는 것이다. - Variational Distribution :
- Posterior Distribution :
- 관측 데이터가 내가 관심있어하는 Random Variable일 확률 분포
따라서, Posterior Distribution과의 KL-Divergence가 최소가 되게 하는 Variational Distribution을 찾아야 한다.
Posterior를 알 수 없는데 어떻게 Variational을 최대한 가깝게 만들 수 있을까? 마치 Target값을 모르는데 Loss값을 구하라는 것과 같이 느껴진다.
이 문제를 해결하는 것이 ELBO이다. 수식은 아래와 같다.
궁극적인 목표는, Vari와 Post의 KL-DIV를 줄이는 것인데, 아래의 식은 Exact하기 때문에, ELBO(Evidence of Lower Bound)를 Maximize하는 것으로 KL-DIV를 줄이는 효과를 볼 수 있다.
ELBO는 아래와 같이 Reconstruction Term과 Prior Fitting Term으로 나눌 수 있다.
Reconstruction Term은 Auto-Encoder의 Loss로 작용(Minimize시켜야 함)한다.
Prior Fitting Term은 latent distribution(q)을 prior distribution(p)과 비슷해지도록 한다.
궁극적으로 우리는 관측 x에 대해 latent space z를 찾는 것이 목적이다. 우리는 posterior값을 모르기 때문에 우리는 VI의 ELBO 기법을 활용하여 KL-DIV를 최소화하는 효과를 만들어낼 수 있는 Implicit Generative 모델이다.
어떤 입력이 주어지고, Latent space로 보내서 다시 Reconstruction term으로 만들어지는데, Latent된 Prior Distribution으로 z를 샘플링을 하고, 그 뒤 Decoder를 통해 나오는 이미지들이 Generation Result라고 보는 것이다.
여기VAE에 대해 추가적으로 상세히 설명해보려 한다.
Limitation
- Intractable model (hard to evaluate)
- prior fitting term must be diffrentiable
- 대부분 Gaussian(isotropic) 사용

Variational Auto-Encoder는 prior fitting term에서 KL-DIV를 활용하기 때문에 결국 Gaussian이 아니면 활용하기 힘들다는 단점이 있다.
Adversarial Auto-Encoder
GAN
VAE vs GAN
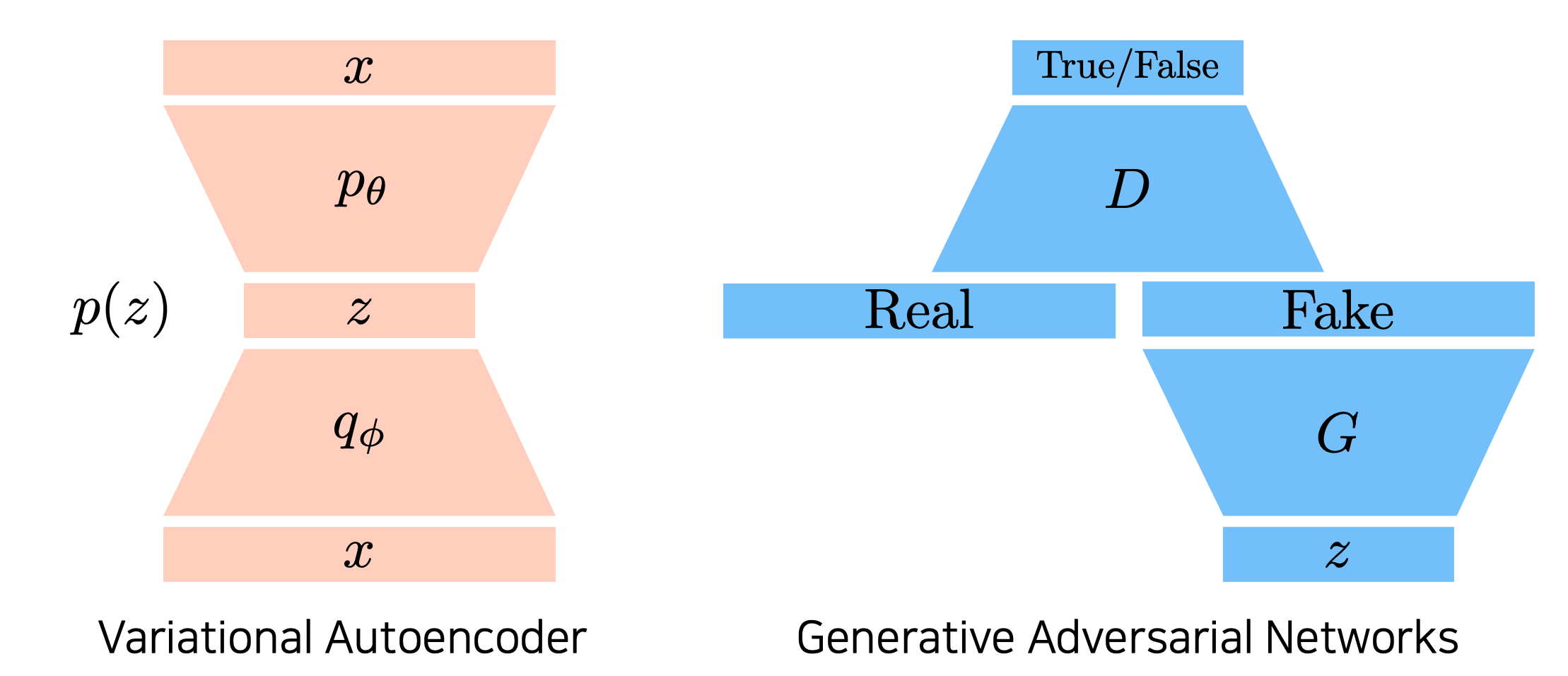
이 글에서 GAN에 대해서 자세히 다루도록 하겠다.
True data Generating Distribution(Data를 통해 우리가 만들어낸 분포)과 내가 학습한 Generator 사이의 Jenson-Shannono Divergence(JSD)를 최소화하는 것이다.
Several GANs
-
DCGAN
Generating images에서는 Deconvolution이 MLP보다 성능이 좋다. -
Info-GAN
학습할 때 Class라는 것을 Random하게 집어넣어서 결과론적으로 gernerting할 때 각 class에 집중하게 된다. -
Text2Image
Dall-E -
Puzzle-GAN
-
CycleGAN(두개의 갠 구조)
-
Star-GAN
-
Progressive-GAN
마스터 클래스
최성준 마스터님
뭘 모르는지 아는 것도 중요하다!
Uncertainty
- data uncertainty(aleatoric uncertainty)
- model uncertainty(epistemic uncertainty)
- Out-of-distribution(novelty detection)
What is Bayesian in DL?
관심있는 대상에 대한 분포를 찾는다.
