Introduction
Generative adversarial networks (GANs)은 기계 학습 분야에서 recent Innovative한 분야중 하나이다. Generative models들은 우리가 지정한 학습 데이터와 매우 유사한 데이터를 생성해낸다. 예를 들면, GANs can create images that look like photographs of human faces, even though the faces don't belong to any real person. These images were created by a GAN:

GANs achieve this level of realism by pairing a generator, which learns to produce the target output, with a discriminator, which learns to distinguish true data from the output of the generator. The generator tries to fool the discriminator, and the discriminator tries to keep from being fooled.
GAN(Generative Adversarial Network)
강의 영상을 참고했다.
"Generative" describes a class of statistical models that contrasts with discriminative models. Generative models can generate new data instances.
Formally, given a set of data instances X and a set of labels Y: Generative models capture the joint probability p(X, Y), or just p(X) if there are no labels.
In GAN, Discriminative Model can capture p(Y | X)
예를 들어 우리는 어떠한 사진 데이터에 대해서 이를 의 확률 분포로 나타낼 수 있다. 그리고 각각의 의 데이터는 데이터의 어떠한 특징을 나타낸다고 할 수 있는데, 예컨데 이미지 데이터에 안경을 쓴 남성의 비율이 적었다면 안경을 나타내는 어떠한 데이터에 대한 확률 값을 낮게 나타내는 확률 분포를 가지게 될 것이다.
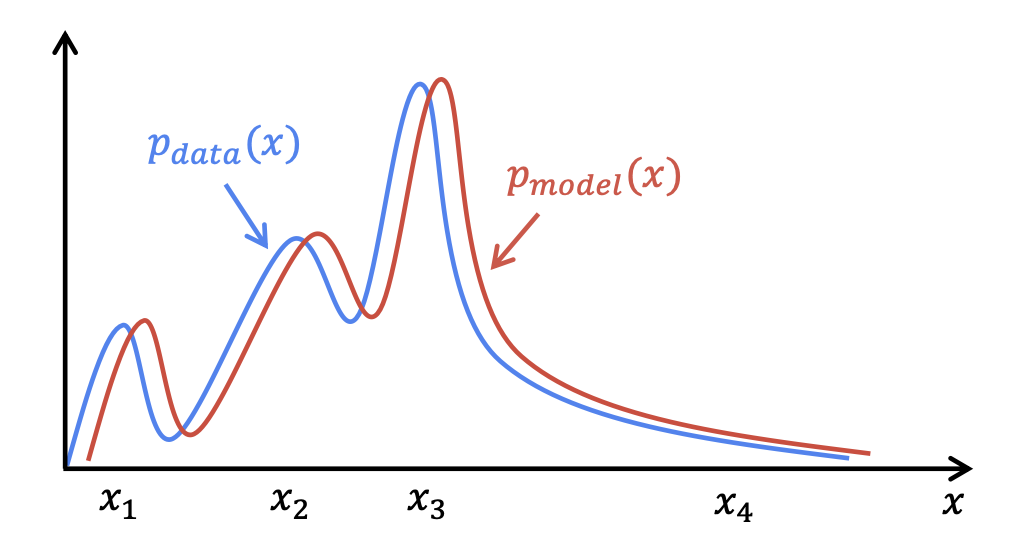
이 때, Generator 모델을 통해 나온 결과물 가 실제 데이터의 확률 분포 와 유사하도록 하는 것이 우리의 최종 목표라고 할 수 있다.
1. Generative Adversarial Network
Adversarial이란 말은 '적대적인' 이란 뜻으로, Generative Model 중에서도 적대적인 방법을 사용하는 GAN(Generative Adversarial Network)에 대해서 알아보자.
기본적인 GAN의 구조는 Discriminator와 Generator로 구성되어 있다. Discriminator는 이미지를 Input받았을 때, Output으로 0또는 1의 1차원 데이터를 출력해주는 Classification모델이다. 대표적으로 Sigmoid 함수를 써서 Threshold를 0.5기준으로 구별한다.

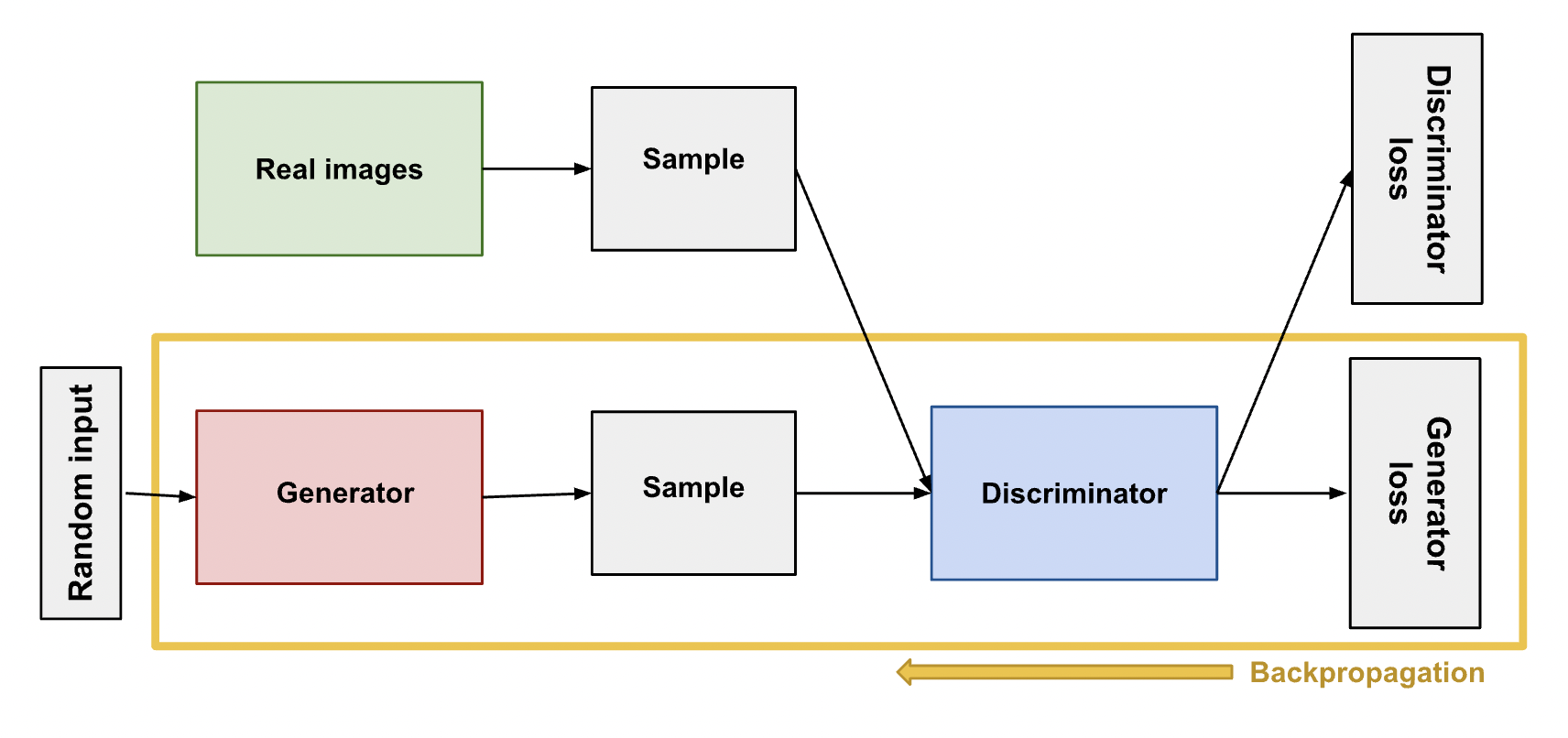
위와 같은 두 가지의 학습을 진행하는 형태로 볼 수 있고, 여기서 Real Image를 x, random input을 z라고 했을 때 Discriminator는 x에 대한 결과값으로 나온 D(x)를 1로 만들고 싶어하고, Generator는 z에 대한 결과값 G(z)에 대하여 D(G(z))가 0이 나오도록 학습하는 것이다. 이를 다음과 같이 수식으로 나타낸다. V는 GAN의 목적 함수이다.
Discriminator
Generator
이를 Pytorch 코드로 확인해보자.
import torch
import torch. nn as nn
D=nn. Sequential(
nn.Linear(784, 128)
nn.ReLU(),
nn.Linear (128, 1),
nn.Sigmoid)
G=nn. Sequential(
nn.Linear (100, 128),
nn.ReLU(),
nn.Linear (128, 784),
nn.Tanh()
criterion =nn. BCELOSS()
d_optimizer = torch.optim.Adam(D.parameters(), Ir=0.01)
g_optimizer = torch.optim.Adam(G.parameters(), Ir=0.01)
# Assume x be real images of shape (batch size, 784)
# Assume z be random noise of shape (batch size, 100)
while True:
# train D
loss = criterion(D(x), 1) + criterion(D(G(z)), 0)
loss.backward()
optimizer.step()
# train g
loss = criterion(D(G(z)), 1)
loss.backward()
optimizer.step()위의 코드에서 우리는 Optimizer로 Binary Cross Entropy Loss를 사용했는데, 이는 아래와 같이 적을 수 있다.
Discriminator 기준으로, 우리는 여기서 y가 1일 때와 0일 때 loss를 더해서 앞서 봤던 수식의 형태를 지닌다는 것을 알 수 있다.(부호가 반대이기 때문에 최소화시키는 형태로 생각할 수 있다.)
한편, Generator의 목적식을 다시 살펴보자.
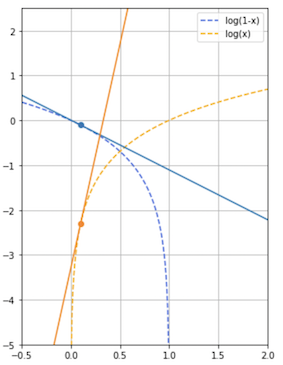
우리는 여기서 학습 초기 단계에서 D(G(z))의 값이 0에 매우 가까울 것이라는 것(가짜에 가까운 형편없는 Output)을 충분히 생각해볼 수 있다. 하지만 D(G(z))의 값이 0에 매우 가까울 때에 의 Gradient의 크기가 충분히 크지 않아 우리는 다음과 같이 수식을 바꿔주게 된다.(Heuristically motivated)
왜 기울기가 커야 할까?
시작 단계에서 Generator가 학습할 때 Gradient를 높여주면 Discriminator가 0이라고 확신하는 단계에서 빠르게 벗어날 수 있기 때문이다.
0에 가까울 때의 기울기 차이를 비교할 수 있다.
따라서 우리는 Pytorch 코드에서 작성한 Binary Cross Entropy Loss 함수가 y=1을 대입했을 때 변형된 log likelihood가 되는 것을 확인할 수 있다.
추가 설명
에서 을 대입했을 때 나오는 결과인 의 값을 최소화하는 것은 를 최대화하는 것과 같다
Why Does GAN Work?
위에서 구한 수식에 대하여 min, max를 취하는 방법이 통계학적으로 JSD를 Minimize하는, 즉 두 분포 간의 거리를 줄이는 방법이기 때문이다.
여기까지 GAN의 기본적인 형태였고, 여기서 변형된(Variants) GANs들에 대해 알아보도록 하자.
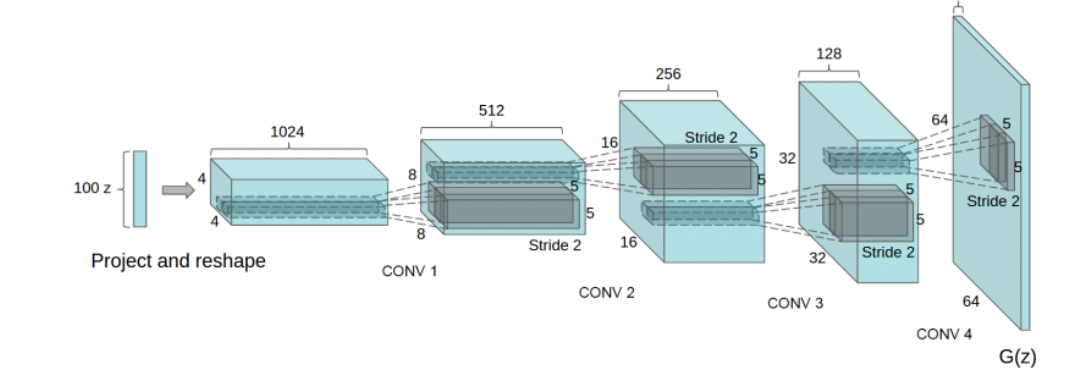
2. DCGAN
Discriminator로 CNN, Generator로 Deconvolution Network를 사용한다.
- pooling layer는 사용하지 않는다.
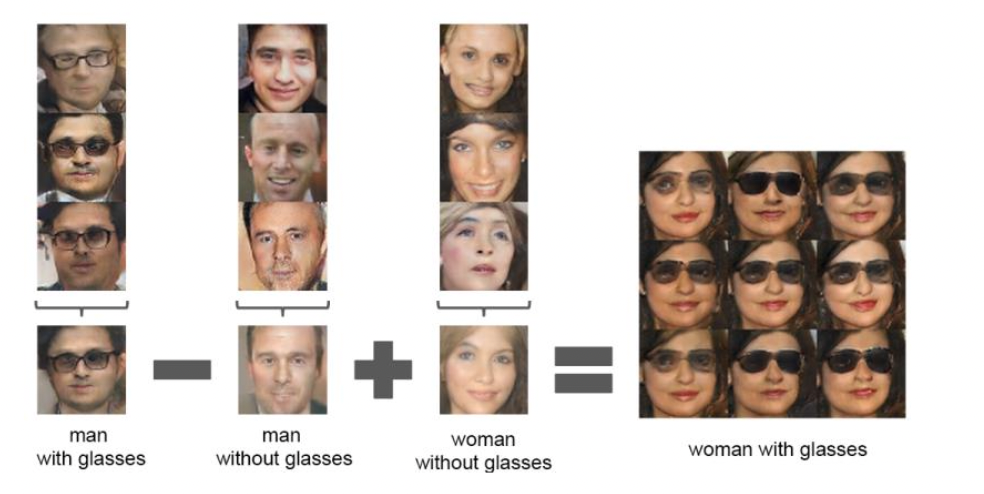
- Latent vectors에 arithmetic이 가능
3. LSGAN
Least Squares GAN(LSGAN)
Proposed a GAN model that adopts the least squared loss function for the discriminator.
-
Discriminator는 D(x)는 1에 가깝게, D(G(z))는 0에 가깝도록 학습하기 위해 Square를 사용한다. Generator또한 D(G(z))가 1에 가깝도록 학습한다.
-
GAN에서는 Discriminator에서 Sigmoid를 사용했지만 여기서는 사용하지 않는다.
-
DCGAN보다 좋은 성능

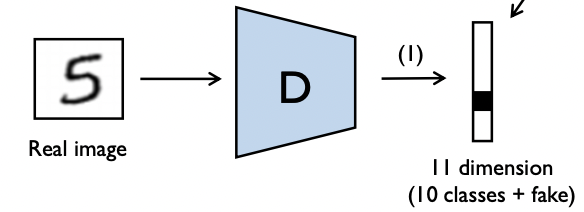
4. SGAN
Semi-Supervised GAN
클래스를 구분하는 GAN이다.
Supervised
Unsupervised
- Discriminator는 이미지가 들어왔을 때 기존의 클래스 + FAKE클래스에 대해 학습하고, Generator는 Latent벡터와 클래스 라벨링 벡터와 함께 입력되어 fake 이미지를 만들어 input으로 들어온 라벨링 벡터로 예측하도록 속여야한다.
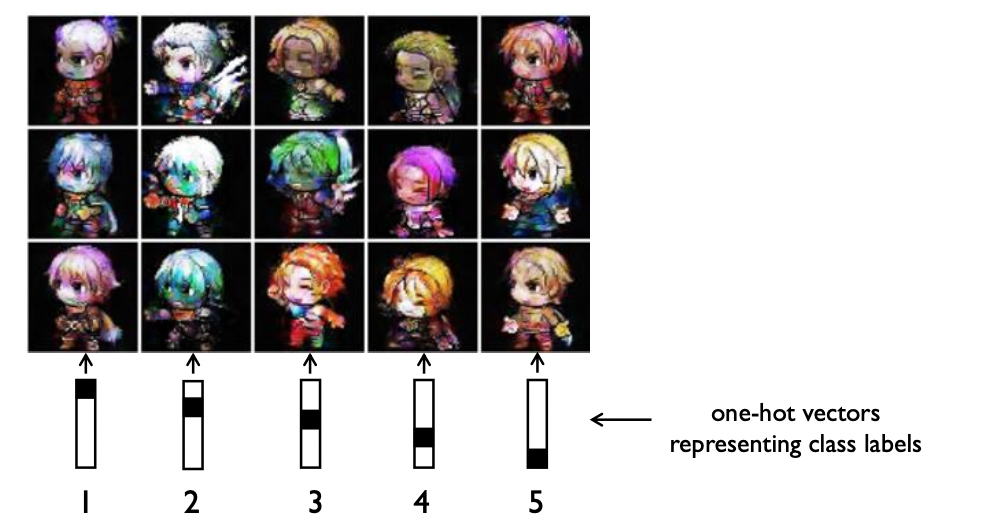
- 위 그림에서 Latent vector가 고정되고 Label데이터가 달라지는 것은 캐릭터가 고정되고 캐릭터의 행동(표정)이 달라지는 형태라고 생각할 수 있다.
5. ACGAN
AC-GAN과 나머지 GAN과의 형태를 비교할 수 있는 그림이다.
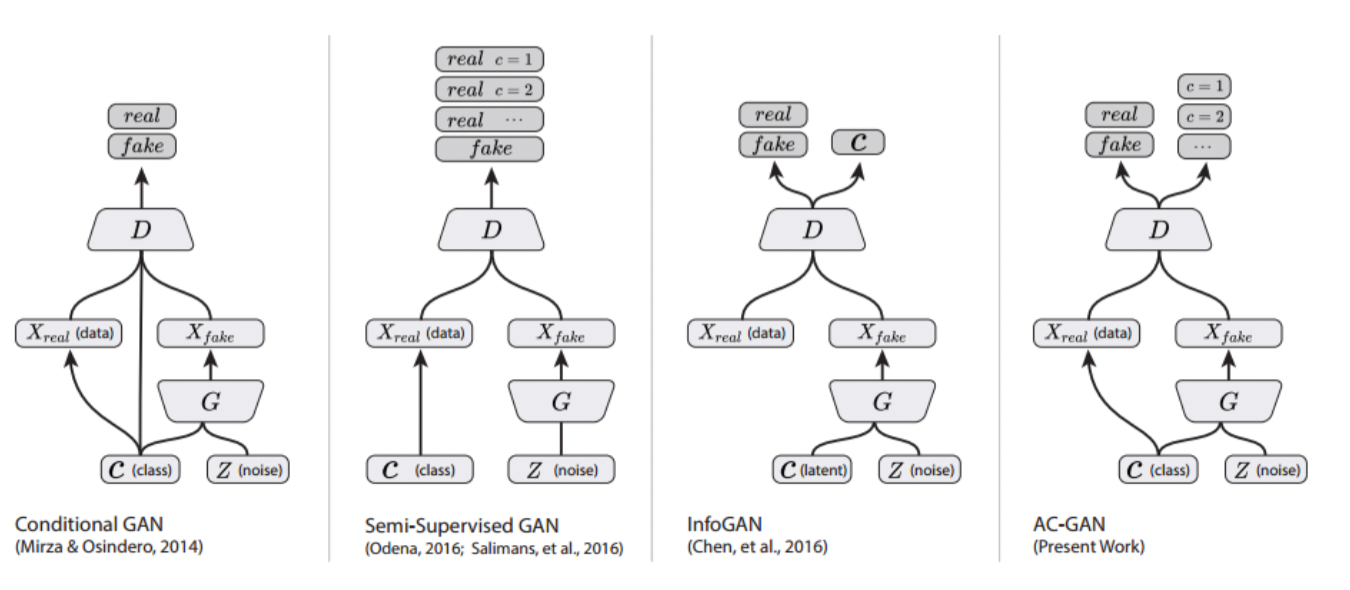
(ACGAN)Auxiliary Classifier GAN
- Discriminator가 해야할 일이 두 개이다.
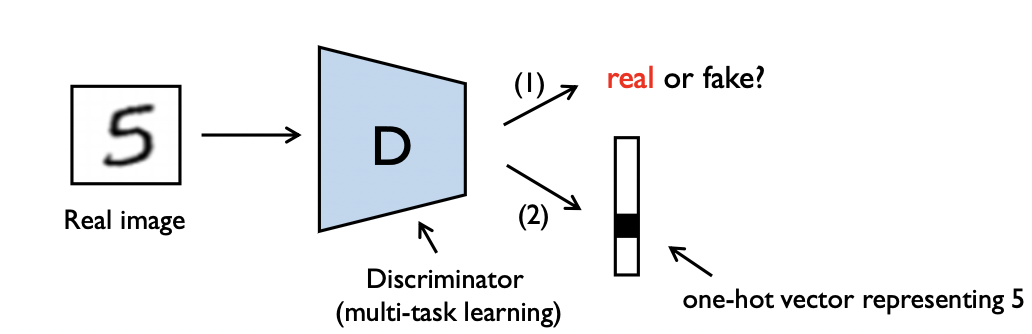
위와 같이 Discriminator는 1.진짜 혹은 가짜 판별과 2.클래스 예측의 두 가지를 학습한다. SGAN에서는 label수가 이었다면 여기서는 class 수와 동일하다. - 나중에 학습이 진행될 수록 성능이 좋아진다.
- Generator보다 Discriminator에 좀 더 초점을 맞추는 것도 좋아보인다.
여기까지 Variants of GAN(Loss의 변환, Label추가)에 대해 알아봤다면, 마지막으로 Extensions of GAN에 대해 알아보자.
6.CycleGAN
Unpaired Image to Image Translation
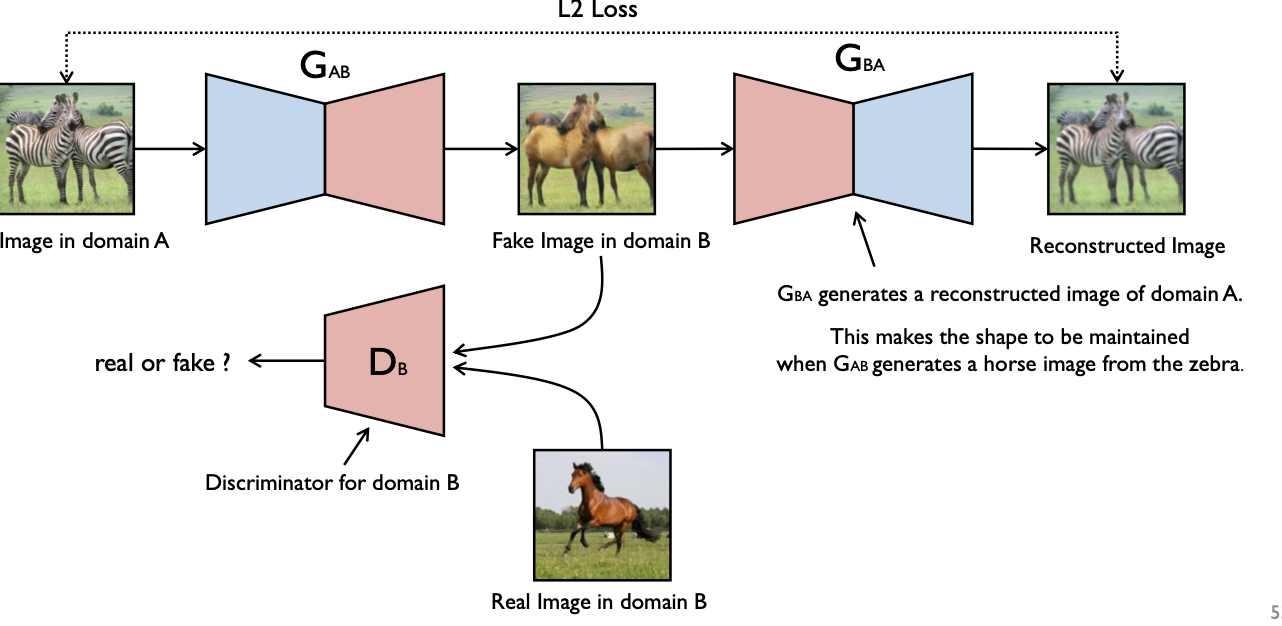
Generator가 이제 image를 입력받는다. Discriminator는 '말'이라고 예측할 수 있도록 학습하고, Generator는 얼룩말 이미지가 들어왔을 때 얼룩 무늬를 뺀 말의 형태를 만들도록 학습한다. 그리고 또 다른 Generator에서 이렇게 생성된 말에서 원래의 얼룩말로 다시 돌렸을 때 실제 입력 얼룩말과의 L2 Loss를 최소화하도록 또 학습해서 얼룩무늬만 제거할 수 있도록 하는 방식이 바로 Cycle GAN이다.
7.StackGAN
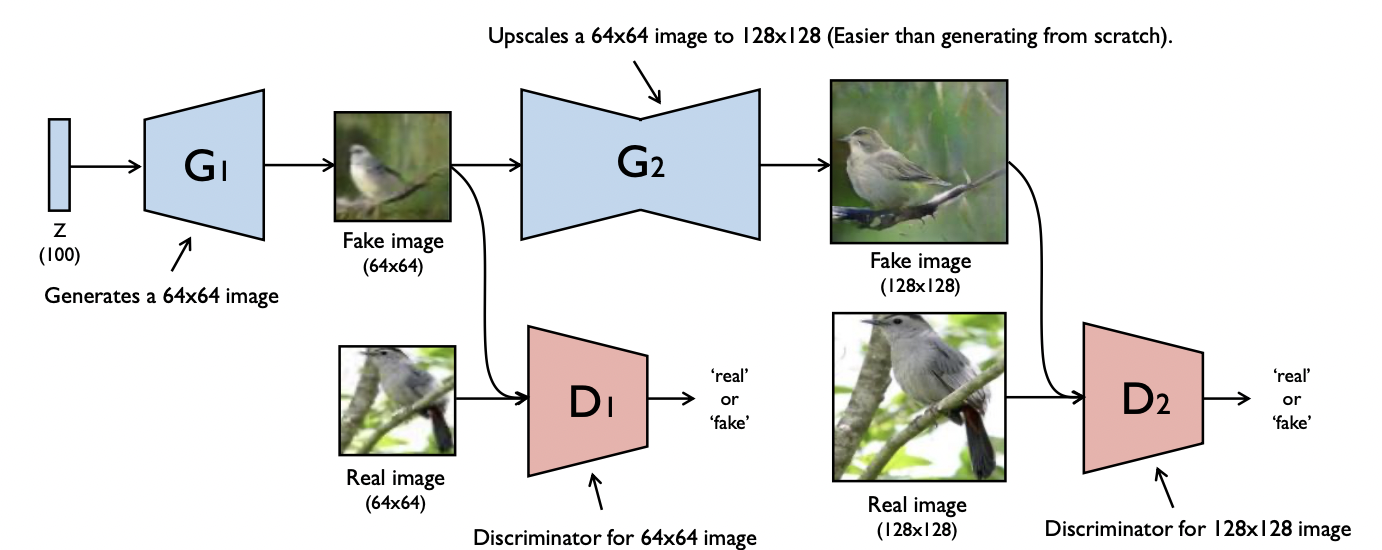
Generator를 한 번 거쳐서 만든 결과물을 가지고 다시 Generator를 거쳐 고해상도의 이미지를 Generate할 수 있는 방법이다. Generator두 개, 각 generating마다 Discriminator한 개씩 총 두 개가 필요하다.