고정 소숫점 & 부동 소숫점

컴퓨터에서 실수를 표현하는 방법은 고정 소수점과 부동 소수점 두가지 방식이 존재한다.

컴퓨터에서는 실수를 정수와 마찬가지로 2진수로만 표현해야 하기 때문에 실수를 표현하는 방법은 정수에 비해 훨씬 복잡하다.

📌 고정 소숫점 (fixed point)

소수점이 찍힐 위치를 미리 정해놓고 소수를 표현하는 방식 (정수 + 소수)

• 3.141592는 부호(+)와 정수부(3), 소수부(0.141592) 3가지 요소 필요함

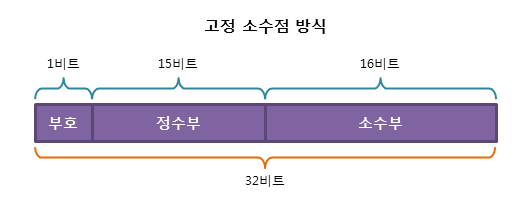
장점 : 실수를 정수부와 소수부로 표현하여 단순하다.

단점 : 표현의 범위가 너무 적어서 활용하기 힘들다. (정수부는 15bit, 소수부는 16bit)

비트 수 대비 표현 가능한 수의 범위가 낮아 실수를 다룰 필요가 있는 범용시스템에서 사용을 거의 하지 않는다.

지수의 값에 따라 소수점이 움직이는 방식을 활용한 실수 표현 방법이다.

소숫점의 위치가 고정되지않고, 앞에서부터 채우며 남은 뒷자리는 다 0으로 채운다.

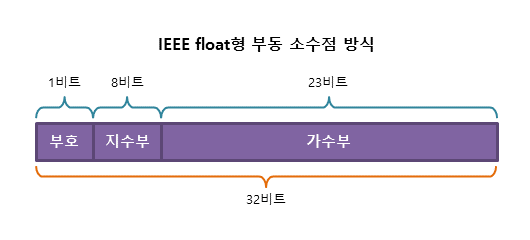
🚘 부동 소숫점 (floating point)

실수를 가수부 + 지수부로 표현한다.

• 가수(Fraction) : 실수의 실제값 표현, 부호화된 고정 소수점 숫자
• 지수(Exponent) : 크기를 표현함. 가수의 어디쯤에 소수점이 있는지 나타냄

예) 10진수 +6132.789 를 표기하면, (가수) + .6132789 (진수) +04 ⇒ +0.6132789 * 10^4

부동소숫점으로 바꾸기

1. 이진법 변환
   0.34(10)을 컴퓨터에서 사용하기 위해 이진수 0.010101110…(2) 로 변환 할 수 있다.

2. 정규형으로 바꾸기

   • 정규형이란 정수 부분에서 한자리수 1만 남기는 것을 말한다.
   • 정수를 한자리 수만 남겨 실수의 표현법을 통일 시킬 수 있다.

   ⇒ 1.0101110… * 2^(-2)

3. 지수부, 초과 표현하기

   • 초과 표현 : N bit에서 2^(N-1)-1을 초과시켜 표현하는 것이다.
   • 1.0101110… * 2^(-2) 를 표현하기 위해서는 지수가 -2 이기 때문에 3을 초과시켜 (-2 +3) 1을 적는다.
   • 지수 영역을 위해서 초과 표현을 사용하면 같은 부호일 경우에는 전체의 비트 패턴을 정수처럼 생각해서 대소 관계를 파악할 수 있게 된다. 실수의 연산보다 정수의 연산이 더 빠르기 때문에 이는 큰 장점.
   • 가수는 1.0101110 이기 때문에 0101110이 되는데, 가수부분으로 4비트를 할당했기 때문에 0101이 된다. *앞의 정수부분 1은, 모든 정규화 수가 1.-으로 시작하니까, Hidden Bit라 하며 정규화 할때 무시하고 쓴다. 따라서 이를 그대로 표현하면- 부호 지수 가수 0 001 0101

💡 부동소숫점의 특징

• 지수부의 크기를 빠르게 비교할 수 있다.
• 부동 소수점은 0과 0.01을 표현하지 못하는 등의 실수를 정확히 표현하지 못하는 오차가 있다.
• 지수와 가수의 상대적인 위치 배치의 문제로, 초과 표현을 사용한다.

장점 : 표현할 수 있는 수의 범위가 넓어진다. (현재 대부분 시스템에서 활용 중)

단점 : 오차가 발생할 수 있다. (부동소수점으로 표현할 수 있는 방법이 매우 다양함)

🔗 참조한 사이트