
🔎 역전파 (오차 역전파)
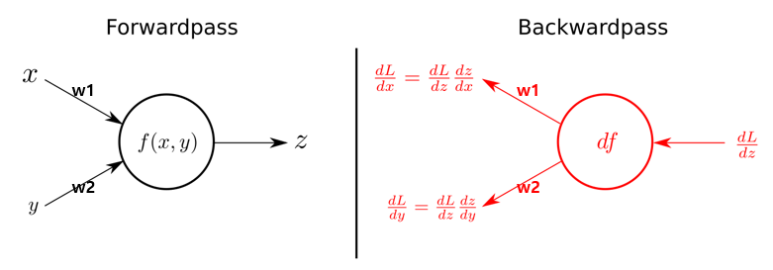
순전파 (Forward Propagation)
신경망의 입력층부터 출력층까지 순서대로 변수들을 계산하고 저장하는 것.
역전파 (Back Propagation)
신경망의 출력층부터 입력층까지 오차를 전파시키며 각 층의 가중치를 업데이트 하는 것.
📌 역전파 과정
1) 주어진 입력값에 상관 없이, 임의의 초기 가중치 w를 준 뒤 은닉층을 거쳐 결과를 계산
2) 계산 결과와 실체 예측 값 사이의 오차를 구함
3) 가중치 업데이트
4) 1~3의 과정을 오차가 더 이상 줄어들지 않을 때까지 반복
기울기 소실 (Vanishing Gradient)
인공지능에게 학습이란, 기울기(Gradient)가 작아지는 방향으로 업데이트를 반복하는 과정을 의미한다. 그런데 시그모이드와 같은 활성화 함수는 미분값이 작기 때문에, 계산 과정 중 가중치가 0에 수렴하여 사라지게 된다. 이와 같은 현상을 기울기 소실이라고 하며, 이를 해결하기 위해 다양한 활성화 함수가 고안되었다. 현재는 ReLU 함수가 가장 많이 사용되고 있다.
🔎 경사하강법 (Gradient Descent)
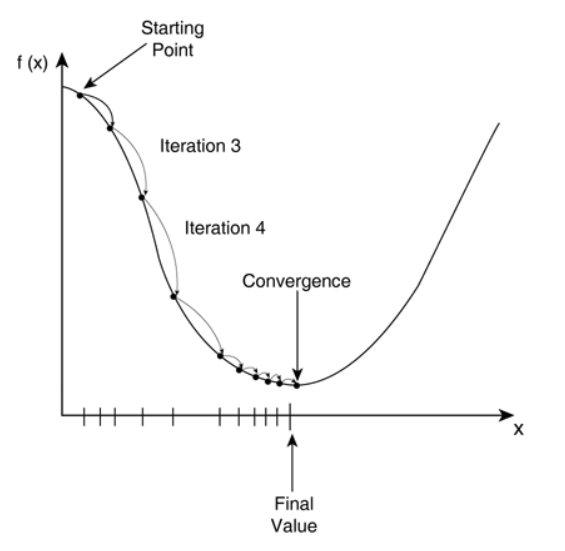
경사하강법이란 1차 미분계수를 이용해 함수의 최소값을 찾아가는 방법이다.
경사하강법의 사용 이유
함수의 최소값을 찾으려면 미분계수가 0인 지점을 찾으면 된다.
그렇다면 왜 함수를 미분하지 않고 경사하강법을 사용해 최소값을 찾을까?
실제 분석에서 마주치는 함수들은
- 닫힌 함수가 아니거나
- 함수의 형태가 복잡하여 (예: 비선형함수)
미분계수와 그 근을 계산하기 어려운 경우가 많기 때문이다.
또 실제 미분계수를 계산하는 것에 비해 경사하강법은 컴퓨터로 구현하기 쉬우며, 데이터 양이 큰 경우 계산량이 효율적이다.
경사하강법 수식
경사하강법은 함수의 경사(gradient)를 이용해 x의 값을 어느 방향으로 얼마나 옮겼을 때 함수가 최소값을 찾는지 찾아보는 방법이다.
💡 최대값(극대값)에 머무르는 경우는 드물기 때문에 고려하지 않는다.
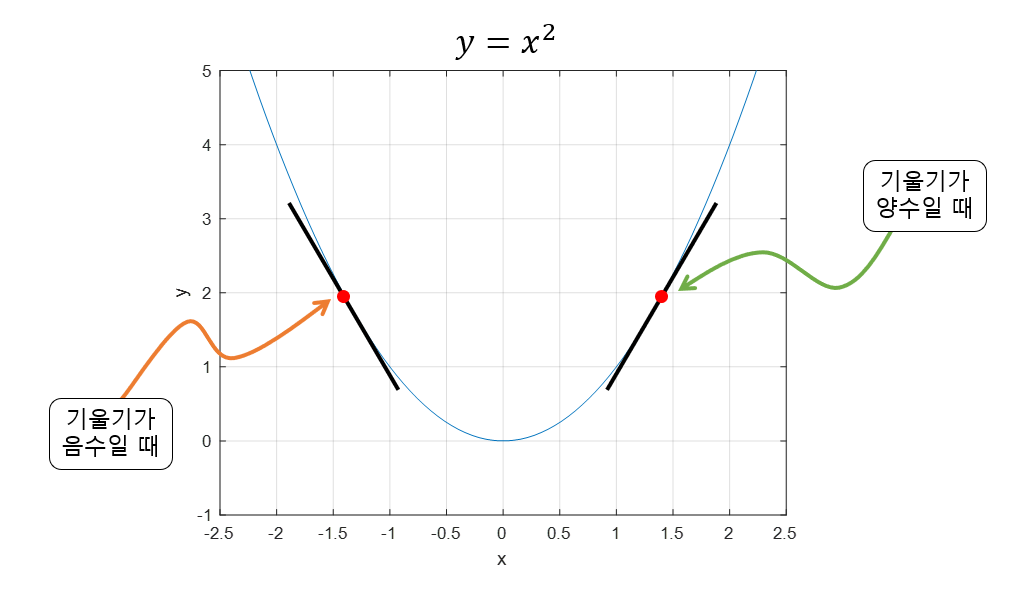
기울기가 양수일 때는 x값이 작아질수록 극소값에 가까워질 것이고,
기울기가 음수일 때는 x값이 커질수록 극소값에 가까워질 것이다.

그러므로 위와 같은 수식을 통해 최소값을 찾을 수 있다.
이동거리(step size)는 어떻게 결정해야 할까?
미분계수는 극소값에 가까울수록 0에 가까워지기 때문에,
- 기울기가 크다면 많이 이동하고
- 기울기가 작다면 적게 이동하는
방식으로 조정하면 될 것이다.
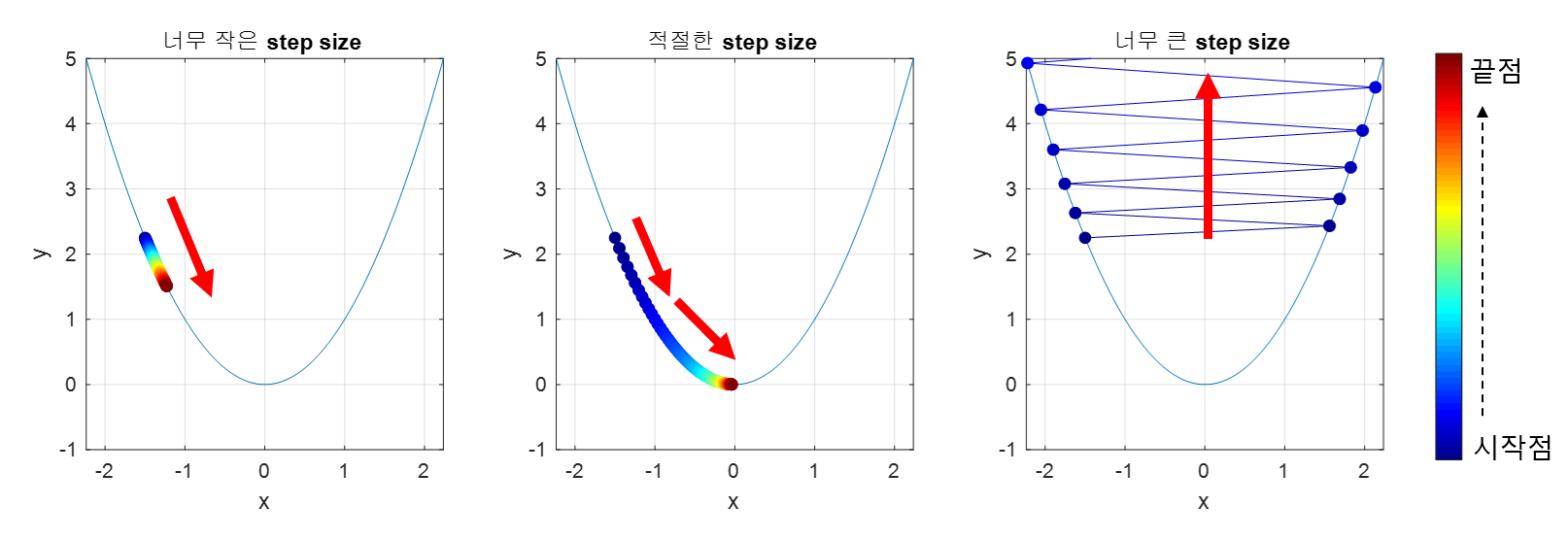
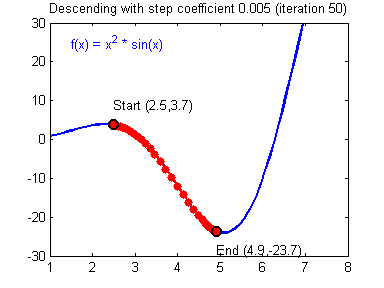
step size를 적절히 조절하지 못할 경우 위와 같은 상황이 발생한다.
경사하강법 최종 수식
α는 step size를 의미한다.
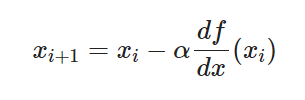
Local Minima 문제
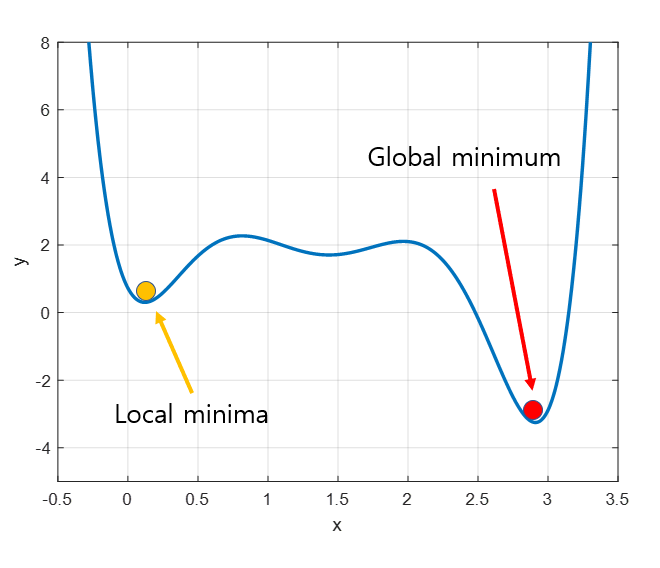
위 사진에서 빨간 점이 최소값이지만, 경사하강법의 시작 위치는 매번 랜덤하기 때문에 어떤 경우에는 local minima에 빠져 올바른 답을 찾지 못할 때도 있다.
📑 참조
https://ko.d2l.ai/chapter_deep-learning-basics/backprop.html
https://www.datamaker.io/blog/posts/32
https://angeloyeo.github.io/2020/08/16/gradient_descent.html
