
회귀 분석
독립변수(x)로 종속변수(y)를 예측하는 것.
체중과 식사량에 관계에 관한 모델을 만든다고 해보자.
체중이 식사량에 따라 달라지는 관계를 확인했다면, 체중은 식사량에 종속되었다고 할 수 있다.
하지만 체중의 변화가 식사량의 변화를 이끌어내는지는 확인하지 못했다.
그러므로 체중은 종속변수, 식사량은 독립변수이다.
독립변수 : 변수의 변화 원인이 모델 밖에 있는 변수
종속변수 : 변수의 변화 원인이 모델 안에 있는 변수
실제 데이터를 바탕으로 학습된 딥러닝 모델은 새로운 입력에 대해 적절한 결과값을 예측해야한다.
이 예측에 이용되는 것이 회귀분석이다.
선형 회귀 (Linear Regression)
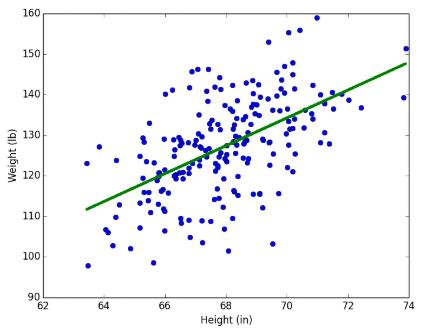
데이터에 대해 가장 잘 설명할 수 있는 최적의 직선을 찾아 분석하는 방법이다.
독립변수 x가 1개라면 단순 선형 회귀, 2개 이상이면 다중 선형 회귀라고 한다.
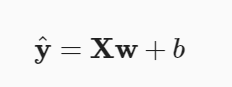
x : 독립 변수. y에 영향을 주는 n개의 변수
y : 종속 변수
w : 가중치. 각 x마다 하나의 w가 존재
b : 편향(bias)
로지스틱 회귀 (Logistic Regression)
연속된 수가 아닌 범주형(categorical) 변수를 예측할 때 사용된다.
이 모델은 범주 A에 속할 확률을 예측한다.
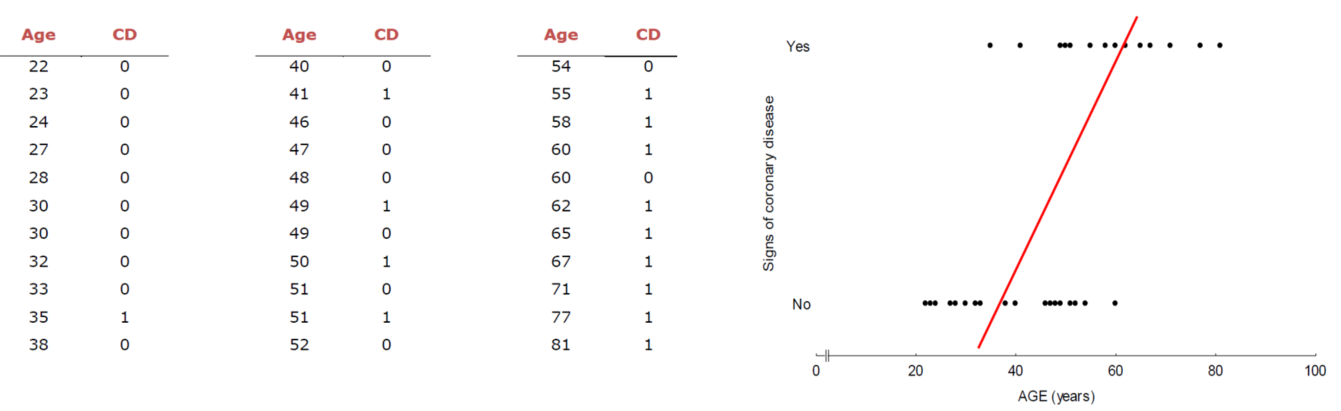
연령에 따른 암 발생 여부(발병: 1, 정상: 0)에 관해 모델을 구축하면, 위 그래프와 같은 모양이 나온다.
선형 회귀로는 적절한 직선을 찾을 수 없다.
이는 종속변수인 암 발생 여부가 중간범주가 없고, 숫자 자체에 의미가 없는 (0과 1을 바꾸어도 되는) 범주형변수이기 때문이다.
이러한 문제 때문에 로지스틱 회귀 모델이 제안되었다.
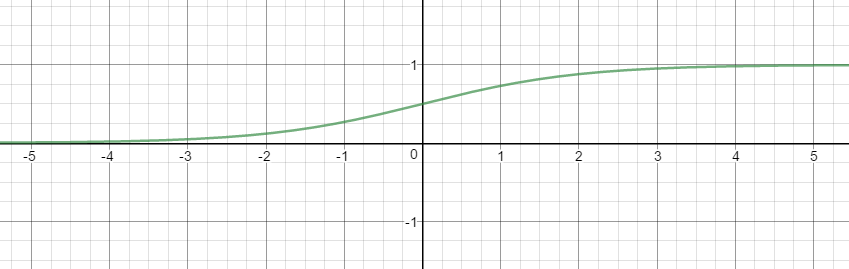
로지스틱 함수는 시그모이드 함수의 다른 이름이다.
로지스틱 함수는 0과 1 사이의 치역을 가지기 때문에 확률밀도함수 요건을 충족시킨다.
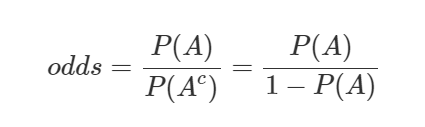
승산(Odds)이란 임의의 사건 A가 발생하지 않을 확률 대비 일어날 확률의 비율을 뜻한다.
승산이 커질수록 사건 A가 발생할 확률이 커지는 것이다.
이렇게 구한 Odds에 자연로그를 취하면 Log-Odds가 된다.
종속변수 y가 범주형 변수이기 때문에 기존 회귀 모델을 적용할 수 없다.
이 때 y를 범주가 아니라, 범주 1이 될 Log-Odds로 두고 식을 변형하면
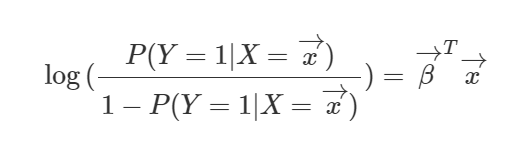
이렇게 된다.
그리고 이 식을 정리하면
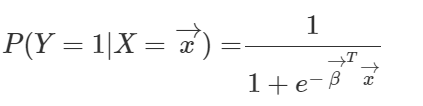
로지스틱 함수의 형태가 된다.
그래서 이 회귀 분석의 이름이 로지스틱 함수인 것이다.
유도 과정은 여기 참고... 난 이해 못했음😭😭😭
로그 손실
로지스틱 회귀에 대한 손실 함수는 로그 손실(Log Loss)라고 부르며, 아래와 같이 구할 수 있다.
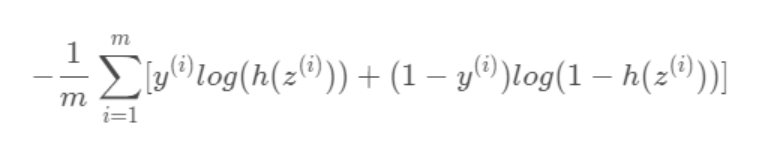
m : 데이터 총 개수
y_i : 데이터 샘플 i의 분류
z_i : 데이터 샘플 i의 Log-Odd
h(z_i) : 데이터 샘플 i의 Log-Odd의 Sigmoid. 즉, i가 분류에 속할 확률
우리는 이 로그 손실을 최소화하는 모델을 찾아야 한다.
이 로그 손실은 사건 A가 일어나는 경우, 아닌 경우 2가지로 나누어 분석해야한다.
- 1) 사건 A가 일어나는 경우 (y=1)
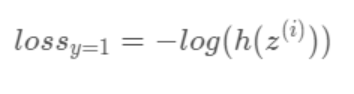
- 2) 사건 A가 일어나지 않는 경우 (y=0)
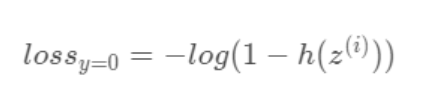
두 손실함수 모두 사건 A가 일어날/일어나지 않을 확률에 로그를 씌운 것 뿐이다.
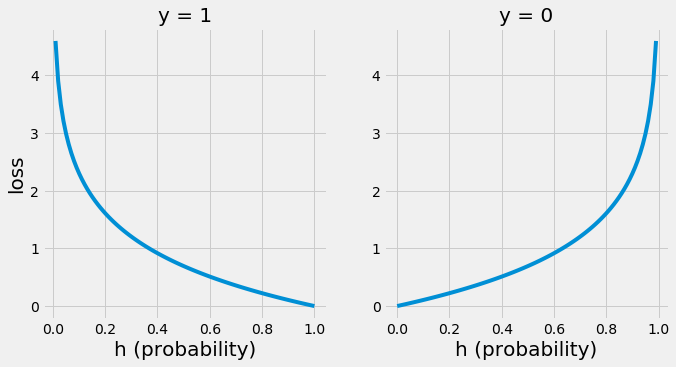
이 때의 손실함수는 위와 같다.
로지스틱 회귀의 최적화에도 경사하강법이 사용된다.
📑 참조
https://mindscale.kr/course/basic-stat-r/regression-intro/
https://ratsgo.github.io/machine%20learning/2017/04/02/logistic/
https://hleecaster.com/ml-logistic-regression-concept/
