👀0.개요
## 💡0.1 데이터 만들기
두가지 데이터를 사용하였는데,
첫번째 데이터는 y = (x-10)(x-20)
두번째 데이터는 y = (x-10)(x-20)(x-30)
데이터를 x범위 0~50 으로 세팅하여 csv파일을 각각 만들었다.
아래의 코드를 통해 쉽게 csv파일을 얻을 수 있었다.
알고보니 CSV 파일은 주어져 있었다.. 그냥 데이터를 좀더 다뤄본걸로 생각하자 ..
🐍makedata.py
#!/usr/bin/env python3
import pandas as pd
import numpy as np
a = 1
b = -60
c = 1100
d = -6000
x_values = np.arange(0, 50, 1)
y_values = a * x_values**3 + b * x_values**2 + c* x_values + d
df = pd.DataFrame({'time': x_values, 'y_measure': y_values})
df.to_csv('3rd_degree_equation_data_2.csv', index=False)
📁1.Average Filter
예측 결과값을 이전 결과의 평균값을 반영하여 추정값을 계산한다.
🐍1.1 파이썬 코드
🐍average_filter.py
#!/usr/bin/env python3
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#input arraylike
class AverageFilter:
def __init__(self, y_initial_measure):
self.df = pd.DataFrame()
self.df['initial'] = y_initial_measure
def estimate(self):
self.y_estimate = []
initArray = self.df['initial'].values
print(len(initArray))
for i in range(len(initArray)):
if (i==0) :
self.y_estimate.append(initArray[i])
else:
value = round(self.y_estimate[i-1]*(i)/(i+1) + initArray[i]/(i+1),4)
self.y_estimate.append(value)
self.df['estimate'] =np.array(self.y_estimate)
def getAverageValue(self):
return self.df['estimate'].values
if __name__ == "__main__":
#read csv file as date frame
#signal = pd.read_csv("filters/data/example_Filter_1.csv")
signal = pd.read_csv("filters/data/example_Filter_2.csv")
#set values
timeValues = signal['time'].values
measureValues = signal['y_measure'].values
#estimate value
y_estimate = AverageFilter(measureValues)
y_estimate.estimate()
plt.figure()
# use date for floating
plt.plot(timeValues, measureValues,'k.', label = "Measure")
plt.plot(timeValues, y_estimate.getAverageValue(),'r-',label = "Estimate")
#set label
plt.xlabel('time (s)')
plt.ylabel('signal')
#settings
plt.legend(loc="best")
#plt.axis("equal")
plt.grid(True)
plt.show()
📊1.2 차트 화면
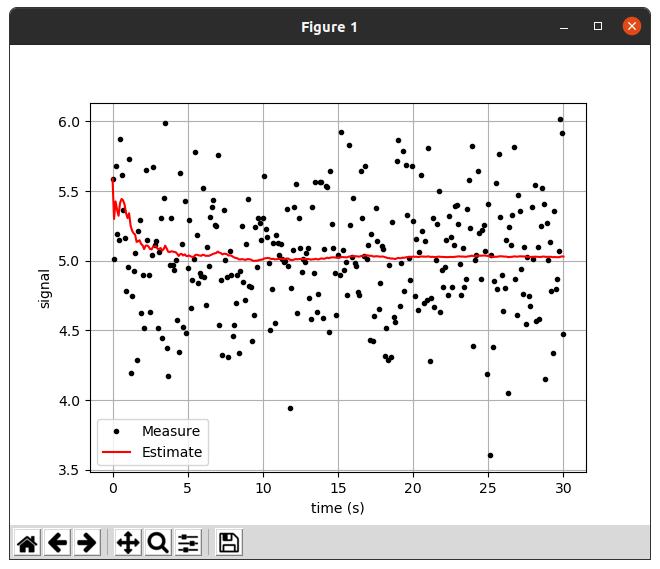
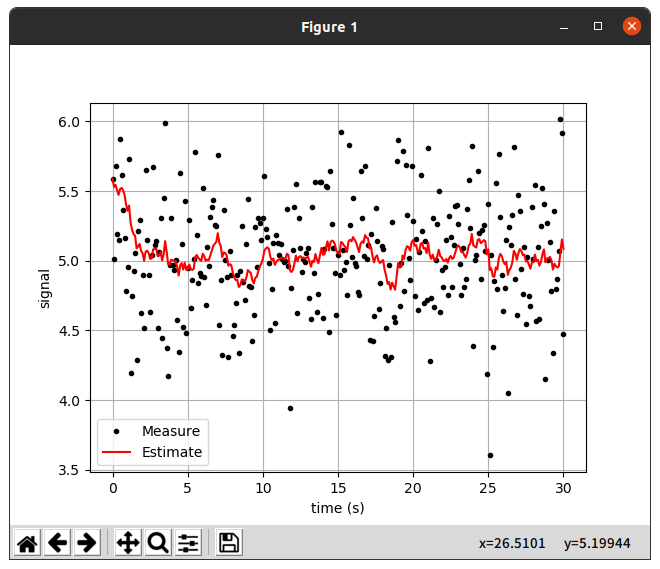
📊first_data chart
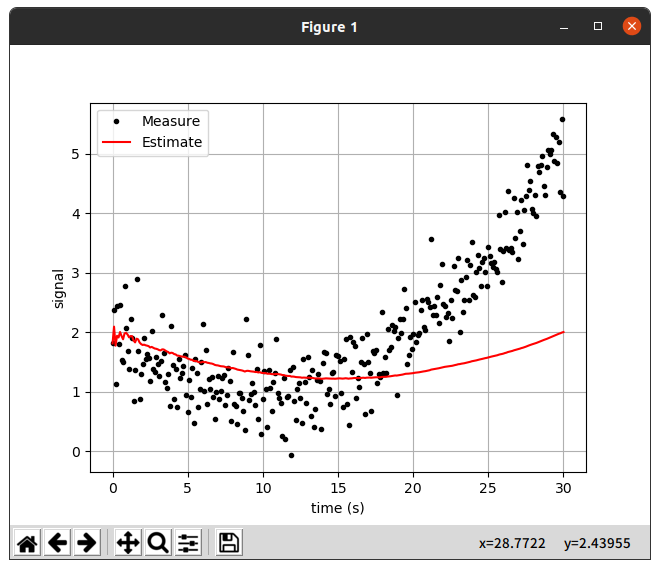
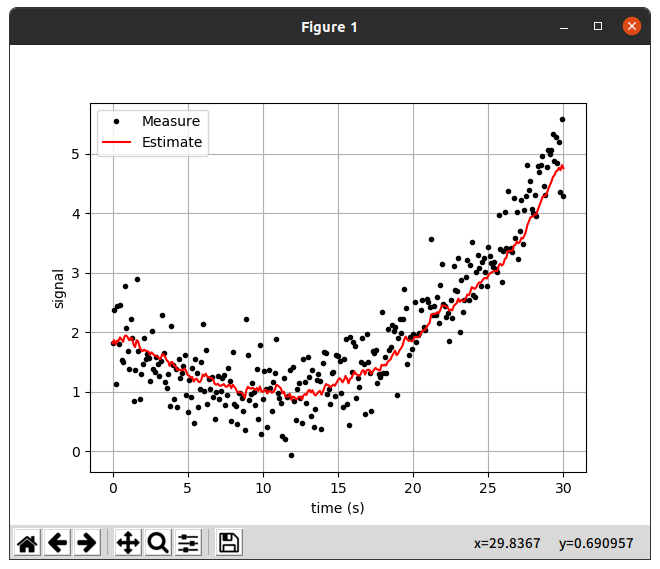
📊second_data chart
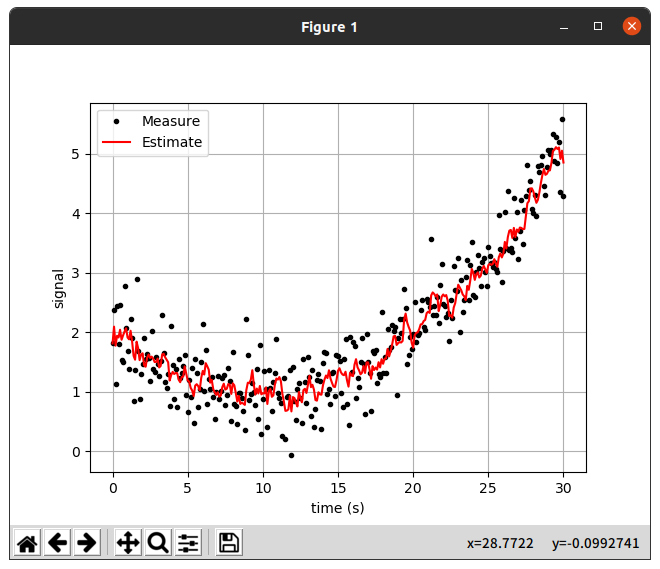
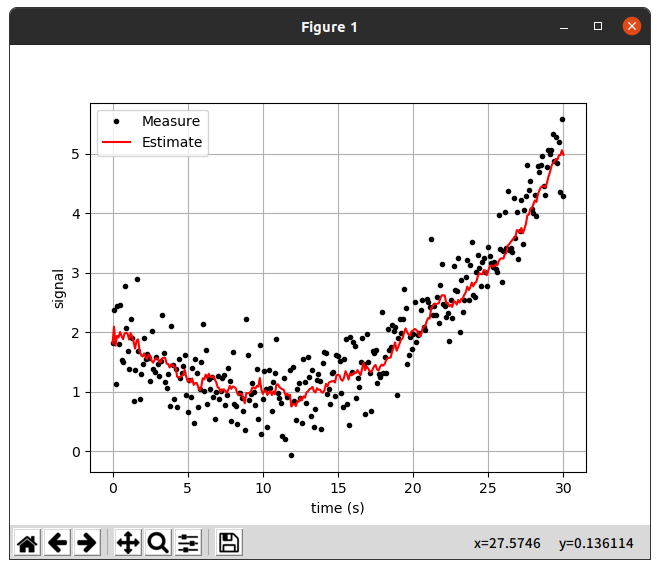
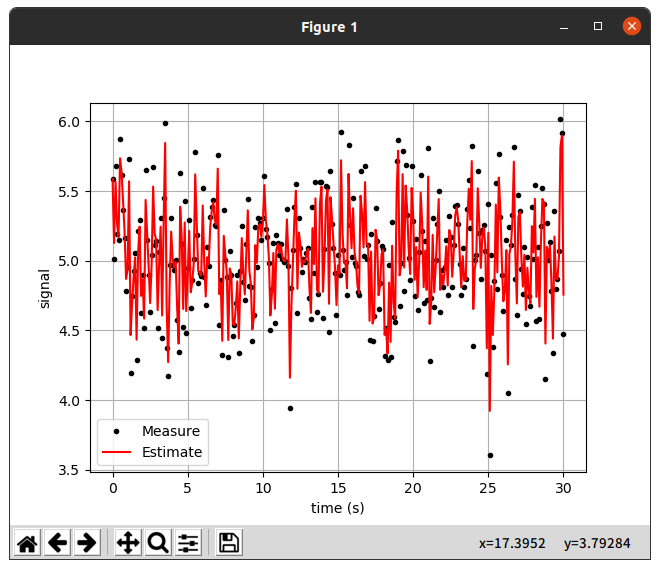
실행결과를 보면 첫번째 데이터의 경우 추정치가 0에 거의 수렴하는 모습이 보였고,
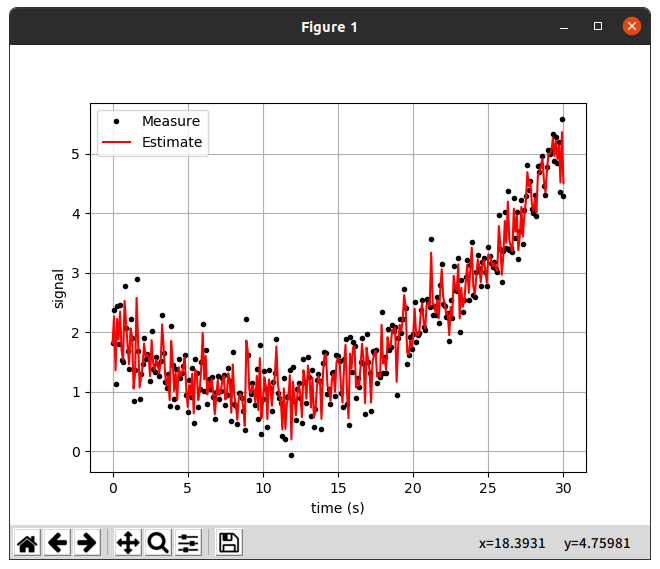
두번째 데이터와 같이 어떤 양상이 있는 데이터에서는 뒤늦게 Data를 따라가는 모습을 보였다.
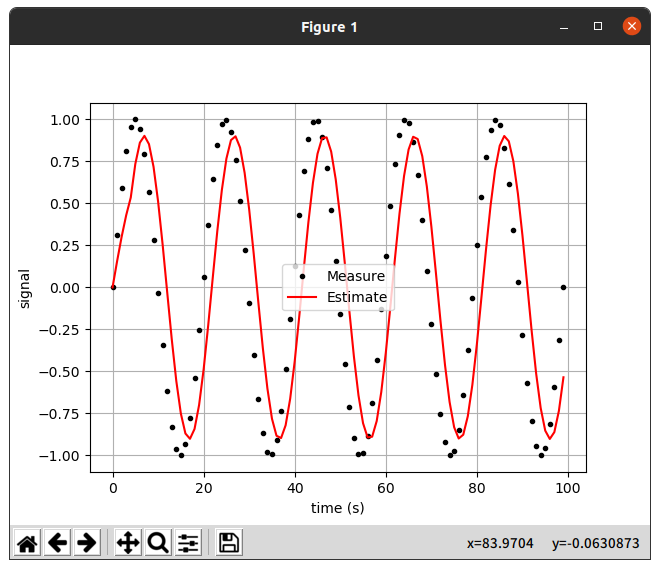
번외로 아래와 같이 sin(x)파를 한번 확인해보았다.
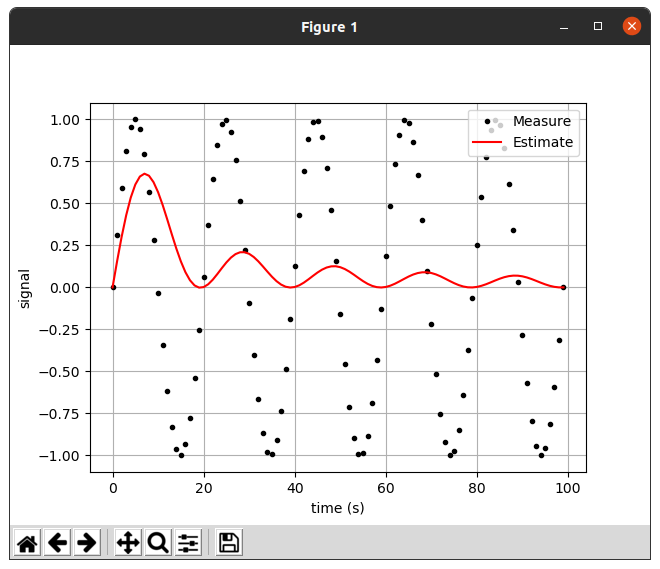
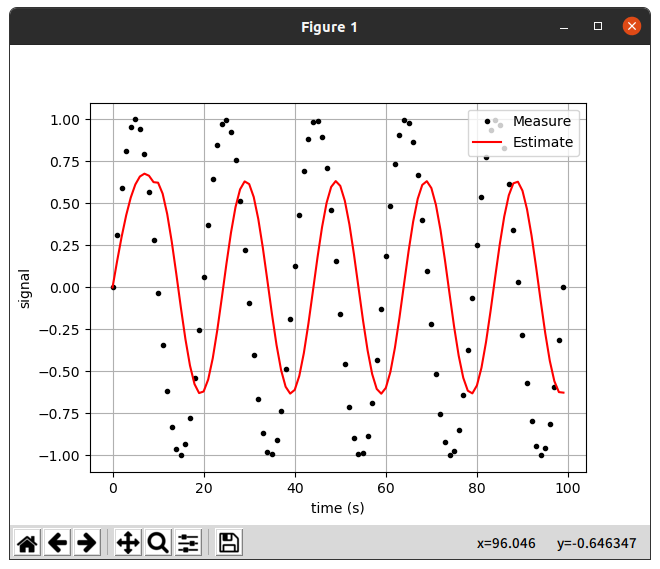
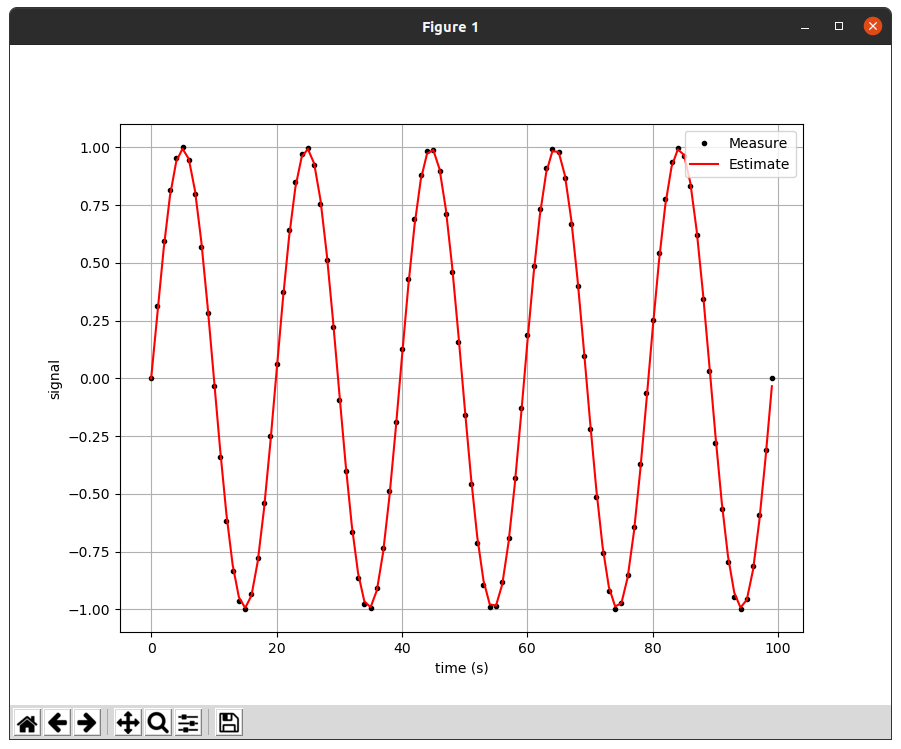
📊sin_data chart
그림과 같이 음수값에서도 추정값은 양수 값을 추정하는 모습을 보인다.
갈수록 추정값이 0에 수렴하는 걸로 보아 sin 파동이 무한정 반복하면 추정값은 한없이 0에 가까워 진다고 추정이된다.
🤔1.3 고찰
Average filter의 확인결과 속도가 너무 느리고 최신데이터를 반영하는 힘이 약해서 굳이 사용하지는 않을 것 같다.
사용을 한다면 일정한 데이터를 수신 받는 도중 큰 노이즈가 가끔 발생하는 경우에 사용할 수 있을것 같다.
📁2.Moving Average Filter
평균값의 구간을 정해서 추정치를 정하는 필터.
🐍2.1 파이썬 코드
🐍moving_average_filter.py
#!/usr/bin/env python3
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
class MovingAverageFilter:
def __init__(self, y_initial_measure, num_average=2.0):
self.df = pd.DataFrame()
self.df['initial'] = y_initial_measure
self.mv = num_average
def estimate(self):
self.y_estimate = []
initArray = self.df['initial'].values
n = self.mv
sum = 0
for i in range(len(initArray)):
if (i == 0 ) :
value = initArray[i]
sum+= value
elif(i < n):
sum += initArray[i]
value = sum/(i+1)
else:
value = self.y_estimate[i-1] + (initArray[i]- initArray[i-n])/n
self.y_estimate.append(value)
self.df['estimate'] =np.array(self.y_estimate)
def getMovingAverageValue(self):
return self.df['estimate'].values
if __name__ == "__main__":
#signal = pd.read_csv("filters/data/example_Filter_1.csv")
#signal = pd.read_csv("filters/data/example_Filter_2.csv")
signal = pd.read_csv("filters/data/sin_function_data.csv")
#set values
timeValues = signal['time'].values
measureValues = signal['y_measure'].values
#estimate value
y_estimate = MovingAverageFilter(measureValues,5)
y_estimate.estimate()
plt.figure()
plt.plot(timeValues, measureValues,'k.',label = "Measure")
plt.plot(timeValues, y_estimate.getMovingAverageValue(),'r-',label = "Estimate")
plt.xlabel('time (s)')
plt.ylabel('signal')
plt.legend(loc="best")
#plt.axis("equal")
plt.grid(True)
plt.show()
📊2.2 차트 화면
2.2.1 MV = 5 일 때
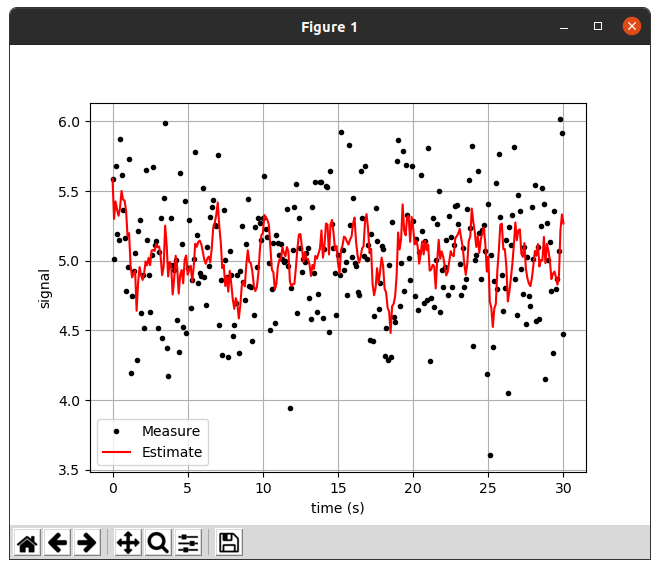
📊first_data chart
📊second_data chart
📊sin_data chart
2.2.1 MV = 10 일 때
📊first_data chart
📊second_data chart
📊sin_data chart
🤔2.3 고찰
Average Filter 보다 새로운 데이터를 받아들이는 수치가 높은 것으로 보인다.
최신의 데이터를 훨씬 더 빠르게 반영하는 것을 확인 할 수 있었다.
그리고 mv 의 수가 높을수록 데이터를 반영하는 속도가 느리고, 진동폭이 좁아진다.
sin그래프와 같이 진동하는 그래프에서 mv가 높을수록 0에 수렴하는 것을 확인하였다.
📁3.Low pass filter
저주파 통과 필터로 최근의 값에 가중치를 높게 줘서 최신데이터의 영향을 키우는 필터이다.
🐍3.1 파이썬 코드
🐍LowPassFilter.py
#!/usr/bin/env python3
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
class LowPassFilter:
def __init__(self, y_initial_measure, alpha=0.9):
self.df = pd.DataFrame()
self.alpha = alpha
self.df['initial'] = y_initial_measure
def estimate(self):
self.y_estimate = []
initArray = self.df['initial'].values
print(len(initArray))
for i in range(len(initArray)):
if (i==0) :
self.y_estimate.append(initArray[i])
else:
value = self.y_estimate[i-1]*self.alpha + initArray[i]*(1-self.alpha)
self.y_estimate.append(value)
self.df['estimate'] =np.array(self.y_estimate)
def getLowPassValue(self):
return self.df['estimate'].values
if __name__ == "__main__":
#read csv file as date frame
#signal = pd.read_csv("filters/data/example_Filter_1.csv")
signal = pd.read_csv("filters/data/example_Filter_2.csv")
#signal = pd.read_csv("filters/data/sin_function_data.csv")
#set values
timeValues = signal['time'].values
measureValues = signal['y_measure'].values
#estimate value
y_estimate = LowPassFilter(measureValues)
y_estimate.estimate()
plt.figure()
plt.plot(timeValues, measureValues,'k.', label = "Measure")
plt.plot(timeValues, y_estimate.getLowPassValue(),'r-',label = "Estimate")
plt.xlabel('time (s)')
plt.ylabel('signal')
plt.legend(loc="best")
#plt.axis("equal")
plt.grid(True)
plt.show()📊3.2 차트 화면
3.2.1 alpha =0.2
📊first_data chart
📊second_data chart
📊sin_data chart
3.2.1 alpha =0.9
📊first_data chart
📊second_data chart
📊sin_data chart
🤔3.3 고찰
1,2차 데이터의 alpha =0.9 인 경우 MovingAverage 와 흡사한 모습을 보였다.
alpha 값이 낮을 수록 최신데이터를 많이 반영하기 때문에 최신데이터와 거의 흡사한 것을 볼 수 있었다.
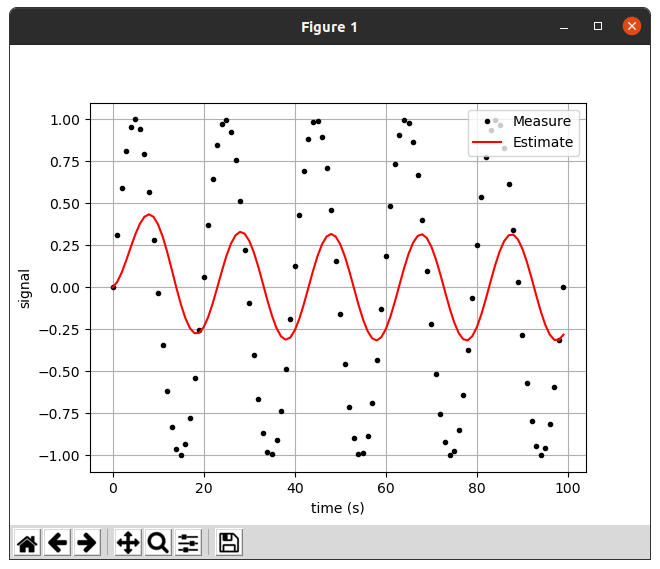
sin과 같이 진동하는 그래프에서 명확한 차이를 볼수 있다.
4. Kalman Filter
5. Comparing Filter
6. Tuning Kalman Filter
7. Kalman Filter(State Space Equation,1)
8. Kalman Filter(State Space Equation,2)
To be Continue