Reference: Derek Hoiem, Alexei Efros, Steve Seitz, David Forsyth, James Hays, Bob Collins

Camera, Geometry and Photometry

Digital Image

우리가 보고 있는 세계는 연속적인 세계다. 그러나 카메라로 이러한 연속적인 세상을 촬영하는 순간, 3차원의 세상이 2차원의 이미지로 projection된다. 이렇게 3D to 2D projection이 일어나는 과정에서 알아야 하는 몇 가지 특징이 있다.

• 연속적인 세계가 디지털로 바뀌면서 불연속적인 수치로 바뀐다
• 각 픽셀은 어떤 특정한 하나의 점을 점유하는 것이 아니라, 어떤 영역의 평균을 계산한 값임
• Capacitor의 용량 문제로 인해 밝기 제한
• 값 자체의 표현 범위가 0-255로 줄어듦

Image formation

인류 최초로 세상을 본뜨고 싶다는 생각을 한 사람의 아이디어는 무엇이었을까?

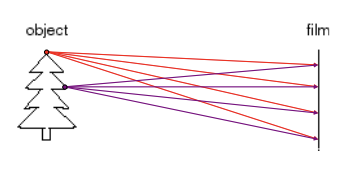
idea 1: 물체 앞에 film을 놓아보자.

당연히 실패다. 물체를 필름에 '인화'한다는 것은 물체의 한 점이 필름의 한 점에 닿게 하는 일과 같다. 그러나, 실제로는 위의 그림과 같이 물체의 한 점은 필름의 전체 면에 닿는다.

Pinhole Camera

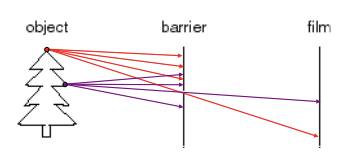
idea 2: film과 물체 사이에 대부분의 빛을 차단하는 목적으로 barrier를 놓아 보자.

barrier는 aperture(조리개)와 같다.

이는 blurring을 줄여줄 수 있으며, 물체의 한 점이 film의 한 점에 닿게 하는 것을 가능케 한다.
그런데 문제가 있다. film에 도달하는 빛의 양이 적어서 굉장히 어둡다는 것이다. 이는 어떻게 해결할 수 있을까?

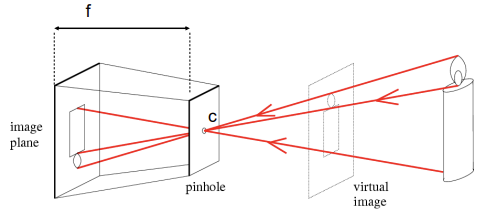
위와 같이 빛을 한 데 모아서 쏴주기 위해 hole에 렌즈를 달면 해결할 수 있다.

• f = focal length
• c = center of the camera
  카메라의 초점 정보는 거리 정보를 담고 있음을 알 수 있다.

Projective Geometry

"카메라로 사진을 찍는다"는 것은 3D 이미지를 2D로 projection하는 것과 같다. 이 과정에서, 우리는 몇 가지 정보를 잃게 된다.

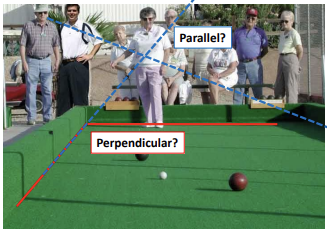
3D to 2D projection을 함으로써 우리는 거리정보와 각도정보를 잃게 된다.

• Length
• Angles

그렇다면, 보존이 되는 정보도 있을까?

• straight lines
  위 그림에서와 같이 직선은 여전히 보존되는 것을 알 수 있다.

Vanishing points and lines

• 관찰자로부터 멀리 있을수록 물체의 크기가 작아보인다.
• flat한 영역에 존재하는 parallel한 직선들은 3차원 상에서 한 점에서 만난다.
• 이 때, line이 만나는 점을 vanishing point라고 한다.

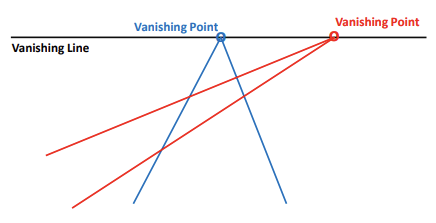
• flat한 영역에 존재하는 parallel한 직선들의 각도를 조금씩 틀면, 무수히 많은 vanishing points가 생긴다.
• 이렇게 모인 수많은 vanishing points를 연결하면, vanishing lines가 된다.

  vanishing lines 뒤로는 정보를 얻을 수 없다. 우리가 흔히 부르는 지평선, 수평선이 이 vanishing line이다.

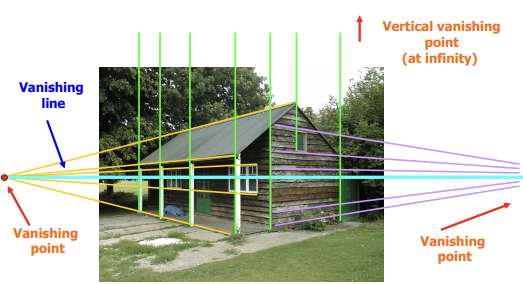
Computervision의 task는 2D image로부터 3D를 reconstruction하는 것이라고 볼 수 있다. 그렇다면, 3D to 2D projection해도 보존되는 straight lines을 가지고 reconstruction을 시도해볼 수 있지 않을까?

• flat한 영역의 parallel lines가 같은 한 점에서 만난다면, parallel line이 존재하는 각기 다른 flat한 영역은 서로 다른 한 점에서 만날 것이다. → 서로 다른 vanishing point를 가질 것이다.
• 위의 그림과 같이 서로 다른 vanishing point를 이용해 이를 어떻게 계산해서 3D reconstruction해볼 수 있지 않을까?

위에 대한 답을 하려면 알아야 할 것들이 너무 많다. 차근차근 알아보자.

Image Geometry

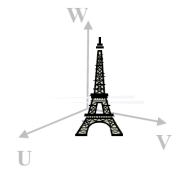
Object of Interest in World Coordinate System (U, V, W)
→ 현실 세계의 coordinate

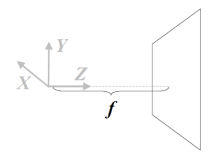
Camera Coordinate System (X, Y, Z)
→ 카메라의 coordinate

• Z는 optic axis(광축)이다.
• 위의 그림은 optic axis을 따라 f 밖에 위치한 이미지 평면을 나타낸 것이다.
• f는 focal length이다.

'현실 세계를 카메라로 찍는다.'
= 'World Coordniate → Camera Coordinate 변환 과정'
=  3D to 3D transformation

3D to 3D transformation을 수행할 때에는 오직 translation과 rotation만 변한다.

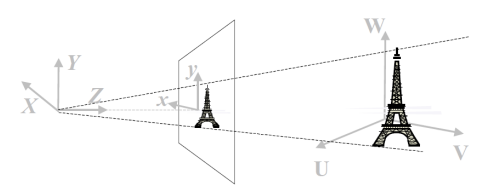
Forward Projection onto image plane.
3D (X, Y, Z) projected to 2D (x, y)
→ 현실 세계를 image plane에 projection (3D to 2D projection)
→ Z 방향에 존재하는 모든 점이 이미지 내 한 픽셀 안에 전부 들어옴.

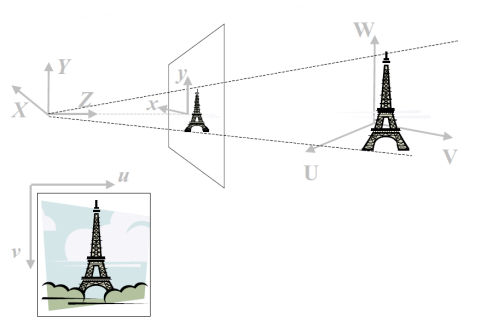
Our Image gets digitzed into pixel coordinates (u, v)
→ 이미지는 픽셀 coordinate으로 transformation되며 디지털화된다.

카메라로 사진을 찍는 것은 'World Coordinate → Camera Coordinate → Image(film) Coordinate → Pixel Coordinate' 변환 과정이다.

그러나, CV의 task는 반대 방향이다. 우리에게 주어진 것은 pixel coordinate이고, 위와 같은 과정을 traceback하여 world가 어떤지 알아내고자 한다. 즉, 한마디로 3D reconstruction을 하고자 한다.
3D reconstruction을 통해 알고 싶은 것은 형상/shape/실루엣, color 등이 있다.

Image Photometry

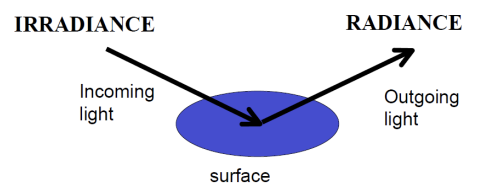
• irradiance : incoming light
• radiance : outgoing light

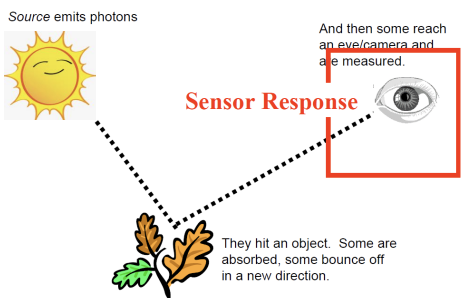
센서(카메라, 눈 등)가 감지하는 것은, 광자가 물체에 부딪힌 뒤 센서에 닿는 시점이다.

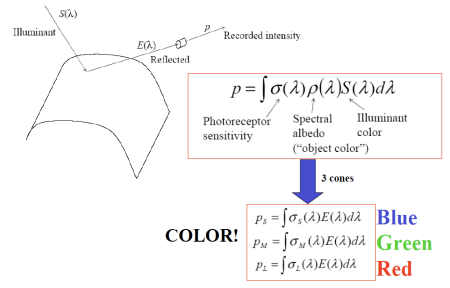
• p : 반사되어 카메라에 기록된 빛
• Photoreceptor sensitivity : 센서의 감도
• Spectral albedo("object color") : 객체의 색
• Illuminant color : 들어오는 빛

요약

• 세상을 이미지화함으로써 연속적인 값이 디지털화되었고, 밝기의 제한이 생겼으며, 표현 범위도 0-255로 줄어들었다. 또한 한 픽셀은 세상의 어떤 점을 표현하는 게 아니라, 어떤 영역을 평균한 값을 의미한다.
• 카메라를 만들기 위해 물체와 film 사이에 barrier를 설치했다. barrier에는 hole이 있었으며, hole에는 빛을 한 데 모아 film에 쏴주기 위해 렌즈를 달았다.
• 3D to 2D projection되면서 길이정보와 각도 정보를 잃었으나, 직선은 여전히 보존됐다.
• '사진 촬영'은 World Cooridnate → Camera Coordinate → Image Coordinate → Pixel Coordinate 하는 과정이다.