Visualizing Images
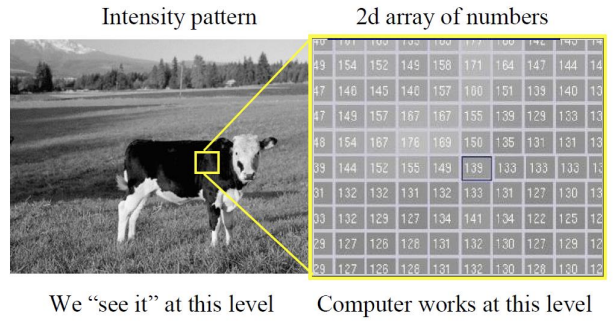
좌측 image는 우리가 실제로 보는 level이다. Computer는 우측 그림과 같이 2d array 형태로 이산화된 level로 동작한다.
3D to 2D projection이 이루어지며 우측 그림과 같이 디지털화되는데, 각 픽셀 하나하나가 포함할 수 있는 영역이 매우 크다.
Images as Surfaces
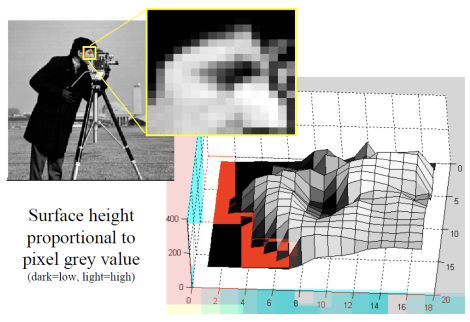
2차원 이미지에서의 밝기 정보는 3차원 상에서 위와 같이 어떠한 형상으로 표현할 수 있다. 높이가 높아질수록 밝기값이 크다는 뜻이다.
밝기 정보를 3차원에서의 형상으로 이해해보자.
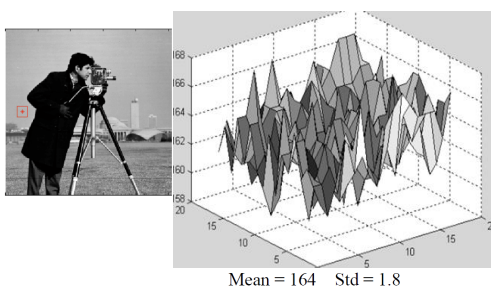
→ 이미지의 배경을 가져와 3차원 형상으로 표현한 그림이다. 높이를 보면 158~168로,값의 변화는 거의 없는 반면 매우 들쑥날쑥한 것을 알 수 있다(high-frequency).
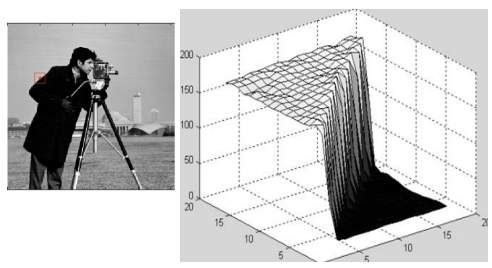
→ object의 edge를 가져와 3차원 형상으로 표현한 그림이다. 높이값의 차이가 커서 마치 언덕처럼 보인다.
→ 이를 통해 밝기값이 큰 부분은 유의미한 object의 단서가 될 것임을 알 수 있다.
이렇듯 밝기 정보를 "높이"로 보고, 이 밝기 언덕을 오르락 내리락하는 개념으로 생각해보자. gradient 벡터를 이용하면 밝기값의 차이가 큰 지점을 알 수 있지 않을까?
Math Example: 1D Gradient
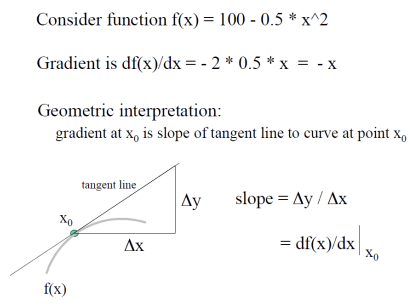
- real world는 continuous한 세상이기 때문에 gradient로 순간변화율 사용
- 하지만, 우리가 다루는 이미지 데이터는 discrete이기 때문에 평균변화율 사용
→ 우리는 discrete data로 continuous world에 approximation할 것을 기억
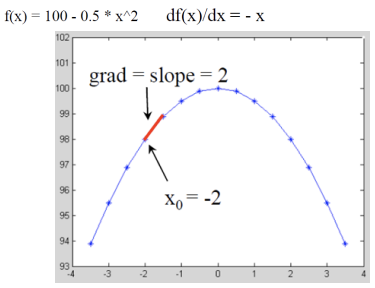
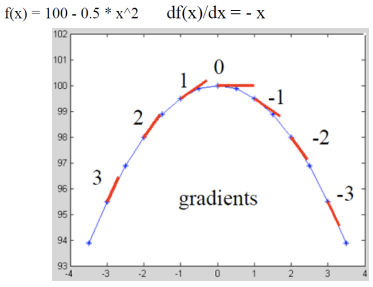
Math Example: 2D Gradient
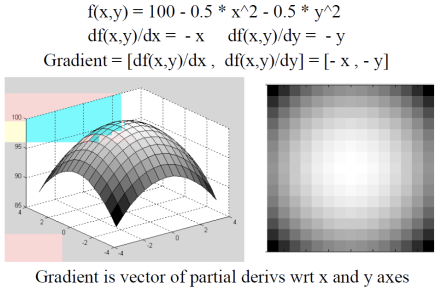
2차원이므로 gradient vector임. vector의 각각의 원소는 x방향, y방향에 대해 편미분한 값임.
우측 이미지와 같이 언뜻 그라데이션같아 보이는 이미지를 보자. 우리는 모든 픽셀에 대해 모든 방향으로의 gradient를 구해서 경사가 큰(gradient가 큰) 영역을 유의미하게 다룰 것이다.

- 화살표의 크기는 gradient의 크기다.
- 큰 화살표에서 작은 화살표 방향으로(gradient가 큰 방향에서 gradient가 작은 방향으로) 모인다.
- 밝기 정보가 높은 곳으로 모인다.
큰 화살표에서 작은 화살표 방향으로 모인다.
= gradient가 큰 방향에서 gradient가 작은 방향으로 모인다.
= 밝기 정보가 높은 곳으로 모인다.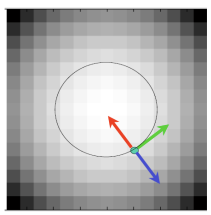
- [red]Vector g points uphill : 경사가 높은 방향
- [blue]Vector -g points downhill : 경사가 낮은 방향
- [green]Vector[g'y, g'x] is perpendicular : green은 constant한 높이의 방향을 나타냄(uphill방향과 downhilll 방향의 접선)
Numerical Derivatives
이제 gradient를 구하기 위해 미분을 할 것이다. 먼저 현재 픽셀과 오른쪽에 있는 픽셀을 가지고 gradient를 구해보자.
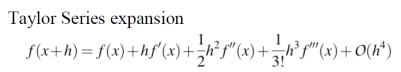
given f(x), O(h^4)는 error를 의미한다. 계산하지 않은 텀에 대해서는 전부 에러로 처리하므로, 어디까지 구하는지는 각자의 선택에 달렸다.
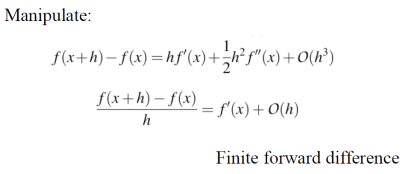
현재 픽셀과 오른쪽 픽셀을 가지고 gradient를 구하면, 에러가 O(h)로 나온다.
O(h)는 h항부터 그 뒤(h, h^2, h^3 ...)는 전부 error라는 의미이다. 이 때 error를 그저 무시하면 안된다. 내가 수용할 만한 에러인지 아닌지 고려해야 함.
**현재 픽셀**과 **오른쪽 픽셀**을 가지고 구한 미분값을 **Finite Forward Difference** 라고 한다.이젠 현재 픽셀과 왼쪽 픽셀의 gradient를 구해보겠다.
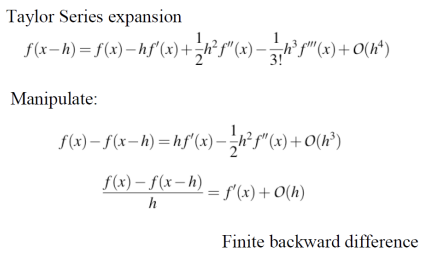
이 때에도 error는 O(h)이다.
**현재 픽셀**과 **왼쪽 픽셀**을 가지고 구한 미분값을 **Finite Backward Difference** 라고 한다.이번에는 현재 픽셀을 기준으로 왼쪽 픽셀과 오른쪽 픽셀의 gradient를 구해보겠다.

위의 이미지를 보면, f(x+h)-f(x-h)를 수행하면, 수식적으로 h^2 텀이 사라지는 것을 볼 수 있다. 따라서 결국에 남게 되는 에러가 O(h^2)이다. 위의 finite forward difference와 finite backward difference의 에러에 비해 한 텀이 사라져서 에러가 원래 수식보다 줄어든 것을 알 수 있다.
수식적으로 error가 한 텀 줄어든 건 알겠는데, 직관적으로 안 와닿아
→ 자연적인 noise에 치우치지 않으며, 조금 더 큰 그림을 볼 수 있기 때문**왼쪽 픽셀**과 **오른쪽 픽셀**을 가지고 구한 미분값을 **Finite Central Difference** 라고 한다.최종적으로, finite forward difference와 finite backward difference보다 finite central difference가 좀 더 정확한 것을 알 수 있다.
Example: Spatial Image Gradients

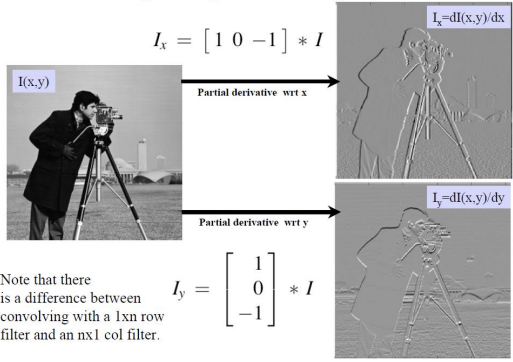
우측 상단 gradient image는 x방향으로 구한 gradient이다. 자세히 보면, 수평 방향으로 경계가 좀 더 뚜렷한 것을 확인할 수 있다. 우측 하단 gradient image는 y방향으로 구한 gradient이다. x방향으로 구한 gradient와는 반대로, 수직 방향으로 경계가 뚜렷한 것을 확인할 수 있다.
0-255 범위에 해당하는 값의 gradient를 구하면 값이 음수와 양수 둘 다 나올 수가 있는데, 이를 어떻게 이미지로 보여준 것이지? 내 의문점이었다.
→ 그냥 이 값들을 적당히 shift해주면 된다. gradient의 중간값이 128로 맞춰주면 보기 좋으니, 이미지 형태로 만들기 위해 적당히 shift해주는 것이다.
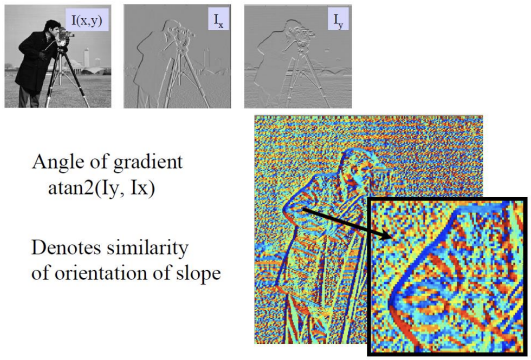
알록달록한 우측 하단 이미지는 similarity of orientation of slope 를 나타낸 것이다. 이는 gradient의 방향(=orientation)을 나타낸다.
- 사람의 오른쪽 팔 부분을 보면 파란색으로 line처럼 칠해진 부분이 있다. 이는 해당 부분은 모두 유사한 orientation을 가진다는 의미이다.
- 반면, 왜 다른 부분은 noise처럼 더러울까? 유사한 orientation을 나타내지 않는 것으로 보아 gradientrk가 크지 않은 영역일 것이다. 그러나 gradient가 작더라도 orientation은 gradinent의 방향이므로 물론 존재하기 때문에 각기 가리키는 방향이 달라서 더럽게 보이는 것이다.
갑자기 값의 변화(gradient)가 큰 부분이 object가 나누어지는 중요한 clue가 될 수 있다. 비슷한 pixel의 연속이라면(gradient가 작다면), 이것은 동일한 객체 내의 픽셀임을 알 수 있음.
More Specifically
우리는 다음과 같이 모든 픽셀 기준 왼쪽 픽셀과 오른쪽 픽셀의 gradient를 구할 것임.
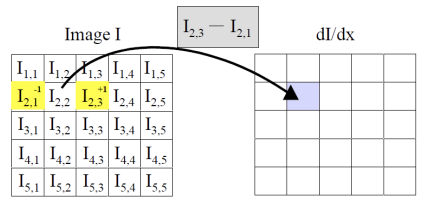
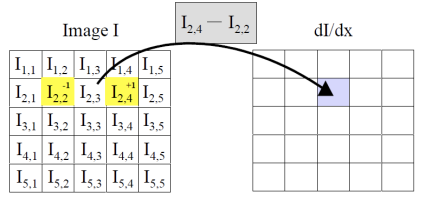
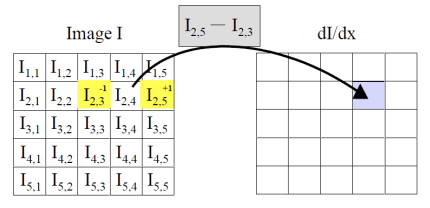
Linear Filter
- general process
origin 픽셀에 weighted sum한 결과로 새로운 이미지를 생성한다 - properties
linear filter의 결과는 input의 선형 함수이다. - example
-smoothing by averaging: form the average of pixels in a neighbourhood
-smoothing by Gaussian: from a weighted sum of pixels in a neighbourhood
-finding a derivative: form a weighted average of pixels in a neighbourhood
Linear의 뜻은 '이웃한 픽셀값들을 linear combination하는 것'을 의미한다.
Linear Filtering
Simplest: 각 픽셀을 이웃한 픽셀들과의 linear combination을 통해 나온 결과로 바꾸자.
The prescription for the linear combination is called the "convolution kernel"
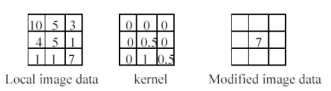
위와 같은 linear combination을 모든 픽셀에 대해 진행할 것이다.
Convolution
이미지 f에 kernel h를 통과시키는 수식(위의 linear combination 과정)을 convolution으로 표현할 수 있다.
Given a kernel(template) h and image f, the convolution h * f is defined as
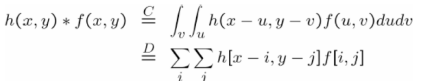
위 수식의 C는 continous, D는 discrete을 나타낸다. discrete에서 i와 j는 인덱스를 바꿔감 모든 픽셀에 대해 계산을 수행한다고 보면 된다.
결과적으로, h는 f와 combining하기 전에 180도 회전한다. 이는 convolution 계산에 의한 것이다. 아래 그림을 보면 이해가 더 쉬울 것이다.
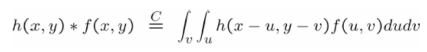
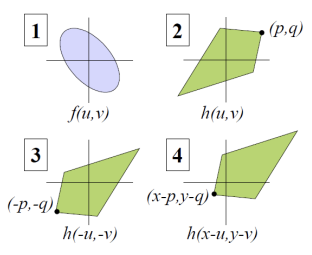
자, 이제 우린 f와 h를 convolution하는 문제까지 도달했다. convolution의 결과로 우리가 원하는 이미지를 얻기 위해서는 컨볼루션 전에 이미지를 좌우반전/상하반전(180도 회전) 해야함.
우리가 왜, 어쩌다 convolution까지 왔는지 흐름을 잘 따라와야 한다.
우린 gradient를 구하는 것이 목적이었음. (gradient는 유의미한 object의 edge를 파악하는 clue가 되므로 구하려고 했었음) gradient는 우리가 '우측 픽셀값 - 좌측 픽셀값'으로 구할 수 있었는데, 이를 filter로 만들어 모든 픽셀을 통과시키자는 idea로 'linear filter' 이야기가 튀어나왔었음.
자, 그럼 linear filter를 convolution 관점에서 해석해보자. linear filter는 이웃한 픽셀과의 weighted sum을 계산해 새로운 값를 얻는 일이다. convolution은 이미지에 kernel을 통과시키는 것을 말하는데, 위 linear filter를 convolution 수식으로 표현하면 좀 편해서 사용하고자 하는 게, 지금까지 설명한 내용이다.
Properties of Convolution
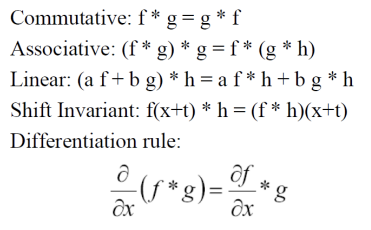
Linear Filtering
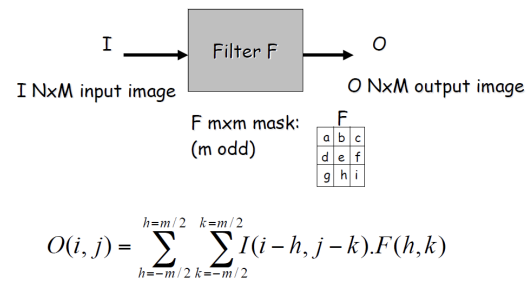
origin pixel에 이웃해있는 픽셀들을 weighted sum하여 새로운 pixel image를 만들어내는 것이 linear filtering이다.
이 과정 convolution을 이용해 수행한다고 했고, convolution은 이미지가 180도 뒤집어져 나온다고 이야기했다.
뒤집지 않고 filtering하는 것을 cross-correlation이라고 한다. cross-correlation을 수행하려면, filter를 symmetric하게 만들어주면 된다.
Finite Difference Filters & Spatial Image Gradients

Problem: Derivates and Noise
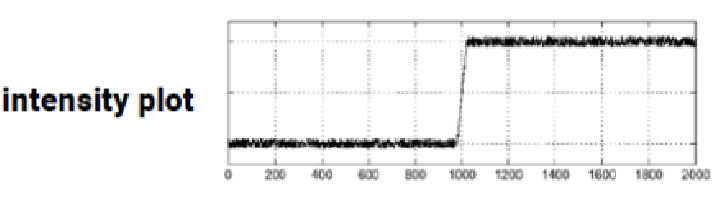
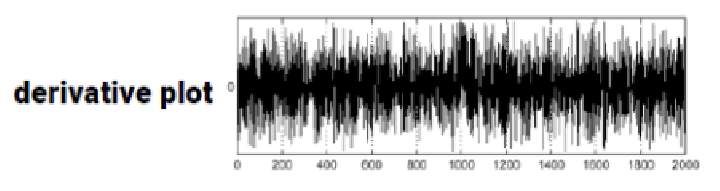
이미지에서 edge를 검출하기 위해 gradient를 구하면, high frequency때문에 에지를 검출할 수 없다.

- 미분은 이미지의 noise를 더욱 증폭시킬 것이다.
- 미분을 할수록 noise는 점점 커진다.
convolution 계산은 noise에 매우 민감하다. 따라서 convolution 계산 전에 noise 제거가 거의 필수이다.
Image Noise
- Fact: images are noisy.
- Noise은 우리가 이미지에서 관심 없는 부분이다.
우리가 제거하고자 하는 noise는 systemetic한 noise이다. 이는 예상 가능한 noise이고, 그 외의 noise에 대해서는 우리가 처리할 수 없다.
Modeling Image Noise
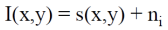
- given I(x,y) : 촬영된 image
- s(x,y) : truth data
- n'i : Gaussian random varibale
noise의 distribution이 왜 Gaussian인가? → 자연 현상의 noise이기 때문
Common Assumptions
- n is i.i.d fro all pixels
- n is zero-mean Gaussian(normal)
zero-mean인 Gaussian noise를 제거하려면? 여러 장의 사진을 averaging한다.
Smoothing Reduces Noise
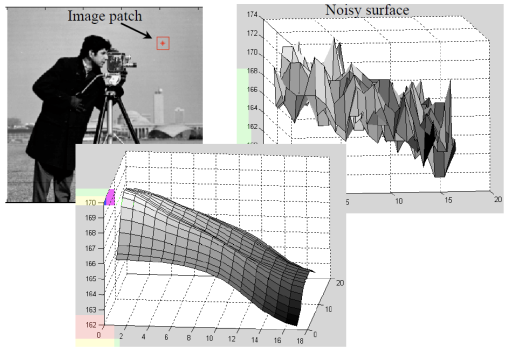
→ noise를 제거하기 위해 smoothing할 것이고, smoothing은 averaging을 통해 할 것이다.
→ 각각의 픽셀로 들어오는 값들을 averaging할 것이다.
그러나 사진이 한장이라면?
→ 카메라의 노출을 열어두면 된다. 그러면 이미지를 연속적으로 수집해서 이들을 averaging한다.
하지만 그럴 수 없는 경우. 어쩔 수 없이 한 장으로 averaging해야 한다면?
→ independent이기 때문에 나와 내 옆 픽셀을 averaging하면 안되나, i이기도 하지만 id이므로... 너와 나의 값이 smooth할 것이라 가정하자(noise도 유사할 것이라 가정)
Averaging / Box Filter
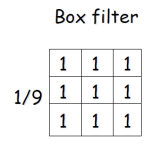
- sum이 1인 filter
- 모든 weight가 동일한 filter를 BOX Filter라고 부른다.
Why Averaging Reduces Noise?
→ 픽셀 noise의 variance보다 average noise의 variance가 더 작기 때문
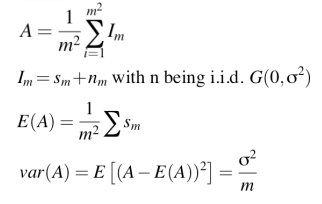
- average noise의 분산 = pixel noise의 분산 / m
Smoothing with Box Filter
- drawback: smoothing은 미세한 image의 detail을 없앤다.

- high frequency : 값의 변화가 큼
- low frequency : 값의 변화가 작음
image의 우측 상단 background 부분에도 지글지글한 high frequency가 존재하는데, 전부 low-pass filtering(Box-filtering)을 진행함으로써 전부 날아가버리면서 smoothing된 것이다.
low-pass filtering: high frequency 날리기
Gaussian Smoothing Filter
idea: 가운데 픽셀이 주인공인데, 모두에게 동일한 값을 부여하는 것은 불공평하다. 가운데 픽셀에게 상대적으로 큰 비중을 줄까?
→ Gaussian Filter
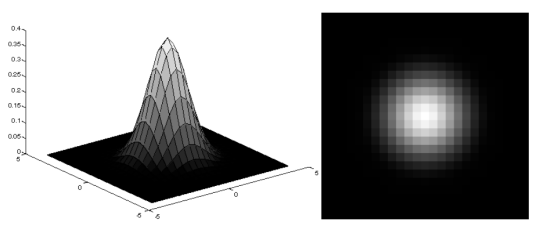
→ 가운데로 갈수록 weight가 높은 filter
요약
- gradient를 화살표로 나타낸 그림을 떠올려보자. 화살표가 클수록 gradient가 크다는 의미이며, 큰 화살표 방향에서 작은 화살표 방향으로 모인다. 이는 gradient가 큰 곳에서 gradient가 작은 곳으로 모인다는 의미와 동일하고, 밝기가 어두운 곳에서 밝은 곳으로 모인다는 의미와 동일하다.
- finite forward/backward difference보다 error가 적은 finite central difference로 gradient를 구하기로 했다. 이를 위해 linear filter 사용하기로 한다.
- linear filtering는 이웃한 픽셀들을 weighted sum한 값을 주인공 픽셀에 새롭게 업데이트해주는 것이다.
- convolution으로 linear filtering을 할 것이다. convolution은 결과가 180도 회전해서 나오기 때문에, cross correlation하기 위해 filter를 symmetric한 것으로 사용한다.
- 이제 gradient 구할 준비를 마쳤는데, 알고 보니 미분이 noise를 증폭시킨다. 그래서 smoothing을 하기로 했다.
- averaging을 통해 smoothing할건데, 처음엔 box filter를 사용했음. box filter는 weight가 모두 동일한 filter를 말함. box filtering을 한다는 것은 low-pass filtering(high-frequency 날리기)을 수행한 것과 같음.
- 그런데 averaging이 왜 noise를 줄였지? pixel noise variance보다 average noise variance가 더 작기 때문.
- box filtering를 하고 보니 가운데 픽셀이 주인공인데, 모두에게 동일한 weight를 주는 것은 불공평함. 그래서 gaussian smoothing filter를 알아봄. gaussian filter는 가운데로 갈수록 weight가 높아지는 filter임.