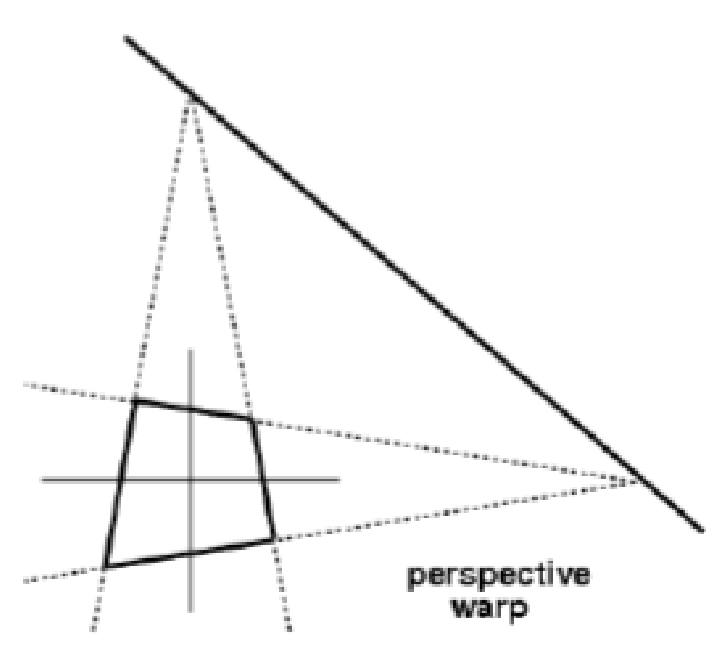
Geometric Image Mappings
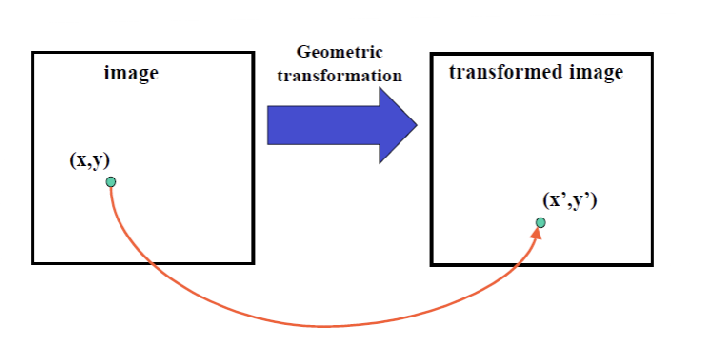
given 2 images
- 2개의 이미지 사이에 어떤 transformation이 일어났을까?
→ correspondence point를 찾고, SPARSE한 각각의 point를 가지고 매핑 관계를 알아내자.
Linear Transformation (can be written as matrices)
Translation
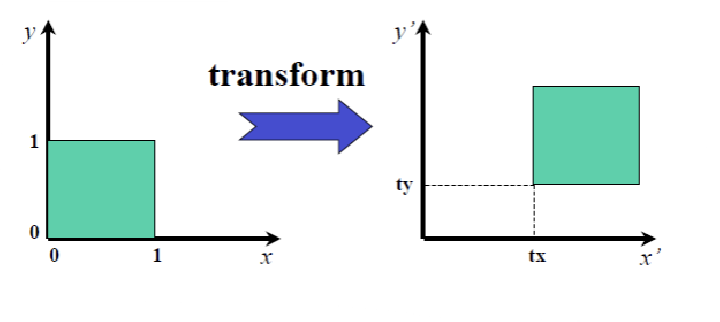
equation:
- x' = x + t'x
- y' = y + t'y
Matrix form
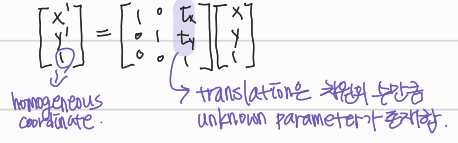
A Simple Stereo System
- Left Camera
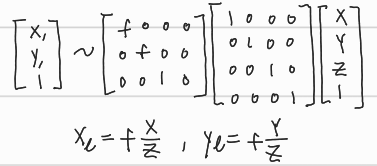
- Right Camera
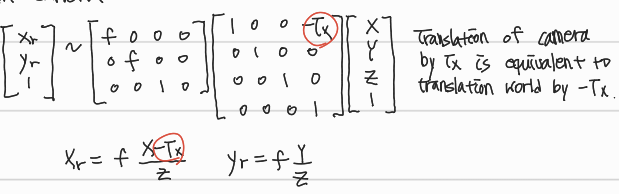
Estimating a Transformation
- General Strategy
Least-Square estimation from point correspondences - Two important(related) questions:
- How many degrees of freedom?
- How many point correspondences are needed?
- Example: Translation estimation
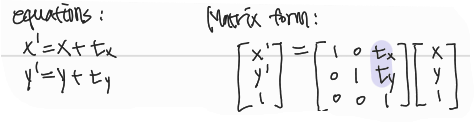
- How many degrees of freedom?
: How many independent variables are there?Two - How many point correspondences are need?
: Each Correspondence (x, y) => (x', y') provides two equations.
DoF / 2 = 2 / 2 = 1
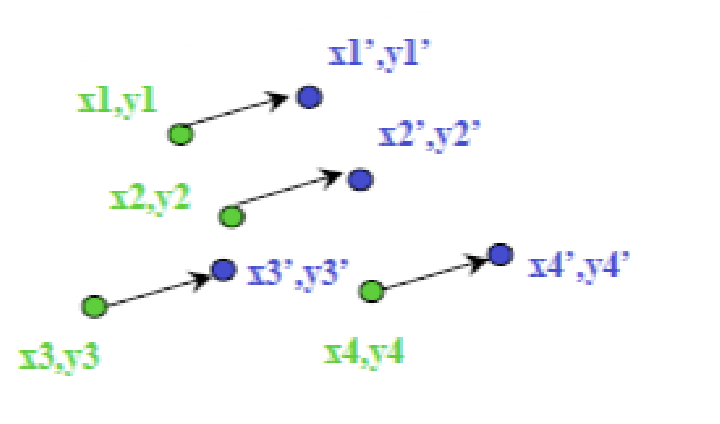
수식적으로는 correspondence point pair 하나만 있으면 되지만, 여러 개의 correspondence point가 발견될 수 있다.
→ 이는 over-determined 문제를 일으킨다.
→ 그렇다면, 여러 개의 points 중 error가 가장 적은 point를 사용해야 할 것이다.
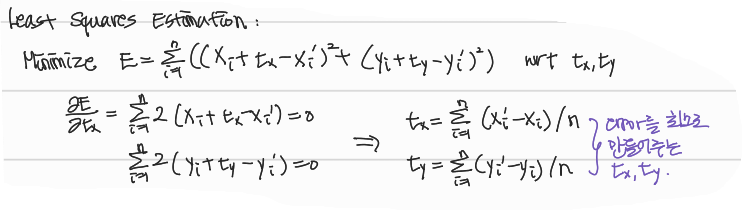
Transformation Groups
우리가 correspondence points를 찾아 추정하기 위한 transformation들은, 이 transformation group에 속해야 한다는 전제가 있다.
1. The set is closed under operator .
_A ∈ G and B ∈ G → A B ∈ G
2. There exists an identity element I such that
_A I = I A = A
3. Each element A has an inverse A^-1 such that
A^-1 A = A A^-1 = I
Why does it matter?
Grous are very well-behaved. When doing computations with groups we can freely compose transformations and assume inverses exist.
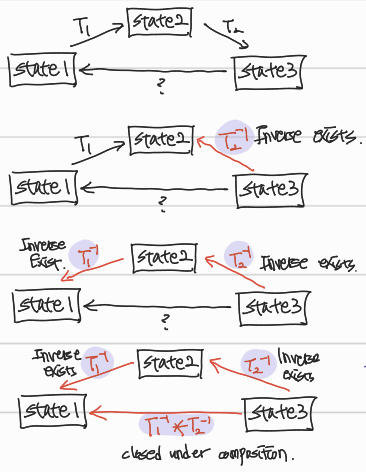
T'1과 T'2 transformation을 했다. T'1^-1, T'2^-1를 통해 state3에서 state2를 거쳐 state1으로 역추적했다. 이를 T'1^-1 * T'2^-1를 통해 한 번에 transformation estimating할 수 있다. 이렇게 composition을 통해서 state1으로 돌아갈 수 있다면, 이 transformation은 closed하다고 이야기한다.
Overview
아래 그림에 존재하는 transformation이 transformation group에 속하는 transformation의 전부다.
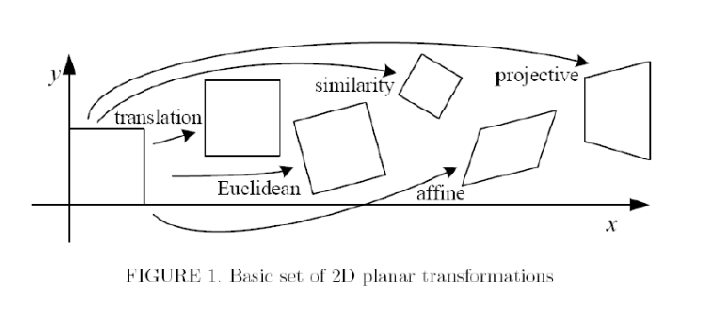
- Euclidean: rigid transformation(translation + rotation)
- similarity: rotation + translation + scaling
- affine: rotation + translation + 부분적으로 scaling
- projective: 3D to 2D transformation
Scale
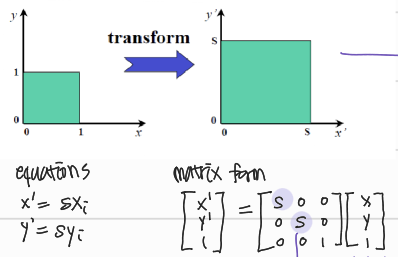
scaling은 좌표축 전에에 있는 것들을 전부 scale한다는 의미임. 그래서 원하는 일을 못할 수도 있는데, 정확히 내가 원하는 만큼 크기를 키우고 싶다면, 원점으로 이동시켜준 뒤에 scaling 진행해야 함.
위 matrix form을 확인해보면, scalability가 같아야 하므로 동일하게 s를 곱해주는 것을 확인할 수 있음.
- DoF: 1
- 구하기 위한 최소 correspondence point pair: 1
Rotation
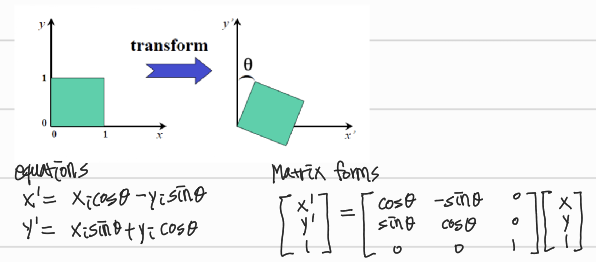
- 2차원
- DoF: 1
- 구하기 위한 최소 correspondence point pair: 1
- 3차원
- DoF: 3
- 구하기 위한 최소 correspondence point pair: 1 (← 하나의 point pair에 3개의 좌표가 나오므로)
Euclidean(Rigid) transformation
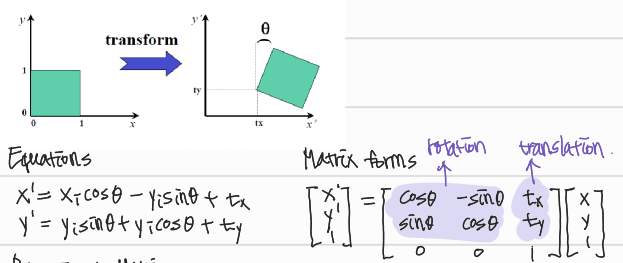
- DoF: 3
- 구하기 위한 최소 correspondence point pair: 2
Partitioned Matrices
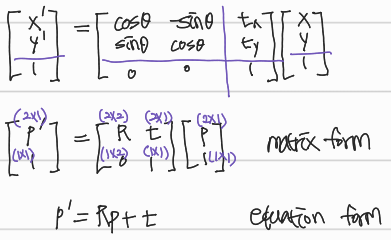
Similarity (scaled Euclidean)
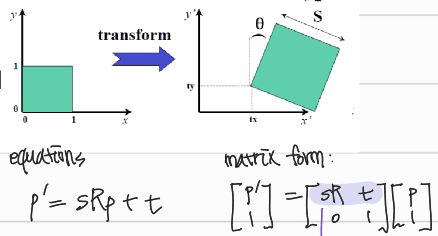
여기에서는 similarity transformation한 p와 p'를 잘 설명하는 parameter를 찾아도 끝이 아니다. 그러한 parameter를 가지는 θ를 찾아야 함.
- DoF: 4 (x, θ, t'x, t'y)
- correspondence point pair 최소 2개 필요
Affine
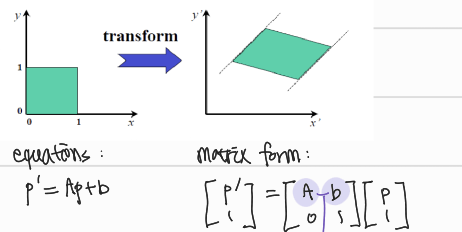
affine은 A와 b에 아무 값이나 다 들어갈 수 있다. 단순히 p'와 p를 잘 설명하는 A와 b를 찾기만 하면 된다.
- DoF: 6
- correspondence point pair 최소 3개 필요
Projective
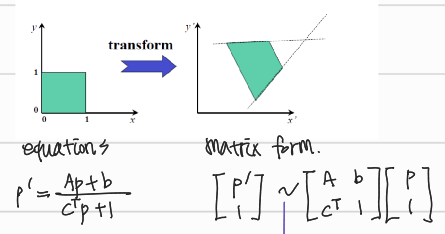
matrix form에서 ~인 이유: scale값은 변형됨. 사실상 scale이 의미 없이 proportional하기 때문
3차원이라면 unknown parameter 15개
- DoF: 8
- correspondence point pair 최소 4개 필요
Summary of 2D Transformation
- Euclidean: rotation + translation
- Similarity: rotation + translation + scaling
- Affine: rotation + translation + aspect ratio + skew
- Projective: rotation + translation + aspect ratio + skew + perspective wrap