여전히 correspondence problem은 남아있다.
아래와 같은 경우 correspondence matching point를 찾기 어렵다.
- flat한 영역
- 전반사(분산이 큰 surface)
- uniform 반사 (Lambertian surface)
따라서 위 경우가 아니며, 지글지글한 texture를 가지고 있는 surface라고 가정해보자.
Matching using Epipolar Lines
이전 시간에 배운 물체의 depth를 파악하는 과정은 다음과 같다.
1) 일치하는 곳(correspondence point)을 찾고
2) disparity 계산
이제 우리가 해야 할 일은 correspondence point를 찾는 일이다.
correspondence point를 찾는 문제는 independent한가?
→ 그렇지 않다. translation한 카메라에서 보이는 영역과 안보이는 영역이 대부분 연속적이기 때문에, 모든 pixel pair 간에 독립적인 일은 아니다.
(예를 들어, 7과 8이 correspondence match되었다면, 그 다음 픽셀은 카메라의 tranlsation을 고려하여 매칭될 곳이 오른쪽에 있을 뿐만 아니라, 9번일 확률이 높다.)
→ 이러한 점이 주는 장단점이 있다.
- 7-8 픽셀을 찾았다면, 8-9 pixel을 continuous하게 같이 결정한다.
- 그러나, 처음부터 잘못 matching한다면, 그 뒤에서까지 모두 일그러져 에러가 굉장히 커질 것
Adding Inter-Scanline Consistency
이제까지 각 left image는 right image의 epipolar line을 따라 독립적으로 matching되었다. 이는 에러를 발생시킬 수 있다.
우리는 동일한 scanline에 있는 matcing에 consistency를 이용할 것이다.
Disparity Space Image
First, we introduce the concept of DSI
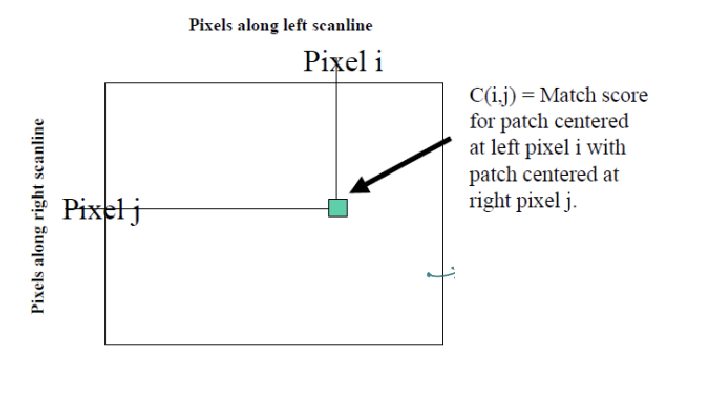
한 row에 대한 DSI는 left와 right image의 한 row를 따라 patch를 옮겨가며, pairwise match scores를 나타낸 것이다.
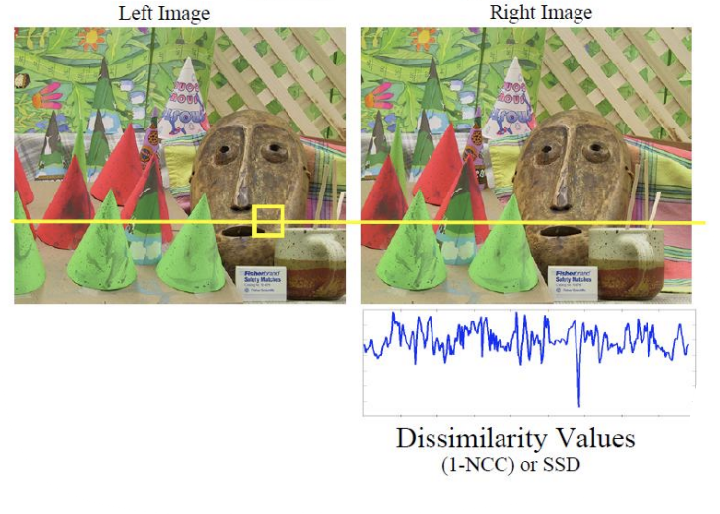
두 이미지의 하나의 row에 대해 각 인덱스별로 similarity를 구한 것이다.
위 그림은 left image의 하나의 patch에 대해 right image에서의 dissimilarity(SSD)를 구한 것이다.
Disparity Space Image

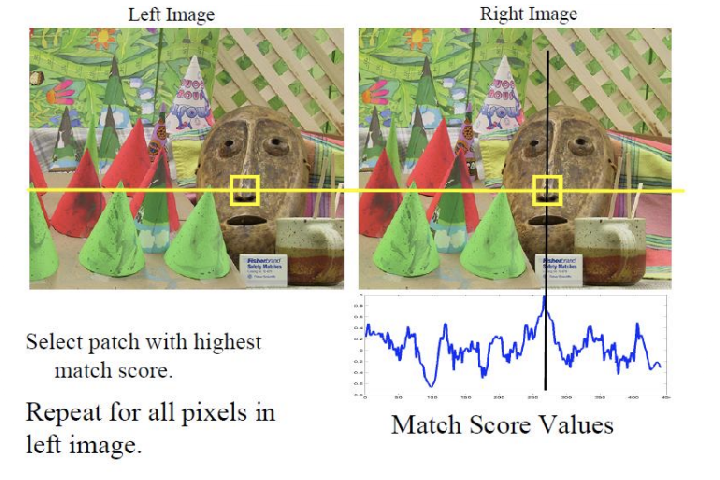
위 이미지와, 앞으로 나올 DSI 이미지는 left와 right이 바뀌었다. 유의해서 보자.
left image의 10번과 right image의 7번이 매칭될 것이다. 왜?
→left image상에서 물체가 왼쪽으로 옮긴 형상이 right image에 나타나기 때문이다.
아, 그렇다면 (7, 10) 위치의 dissimilarity가 가장 작겠구나를 알게 된다. 아하! 그래서 DSI가 완벽한 대각선에 minimum이 있는 것이 아니라, 약간 위쪽에 minimum line이 존재하는 거구나!
대각선에서 멀어질수록 카메라 2대 사이의 거리가 멀 것이다. (== baseline distance가 클 것)
조금 더 정확히는, baseline보다, 두 이미지 사이의 matching point 사이의 disparity에 의해 거리가 벌어진다.
→ 거꾸로, DSI를 보고, base-line distance를 구할 수 있다. 단, 픽셀 하나의 물리적인 size를 알아야 한다.
그리고, 다음 그림과 같이 line이 깔끔하지 않을 수 있다.
- 2번째 그림은 foreground와 background의 급격한 변화 때문에 disparity가 텅 빈 것처럼 표현된다.
1, 2, 3번 중 가장 가까이에 있는 물체는 무엇일까?
→ 3번이다. 두 이미지 사이의 disparity가 커서, 대각선에서 크게 멀어질 것이다(예를 들어 left image에서 50번 픽셀과 right image의 2번 픽셀처럼 disaprity가 크면, parallax에 의해 물체가 가까이 있음을 알 수 있음).- DSI에서 보이는 검은색 큰 네모(disparity 0)는 어디로 이동해도 딱히 변하지 않고, 유사한 flat한 영역일 것이다.
자, 이제 pixel은 continuous할 것이며, independent하지 않을 것임을 알았다. 그러면 이제 우리가 할 일은 optimal path를 찾는 일이다. path값들을 모두 더해서 minimum이 되는 값을 ㅏ찾아보자.
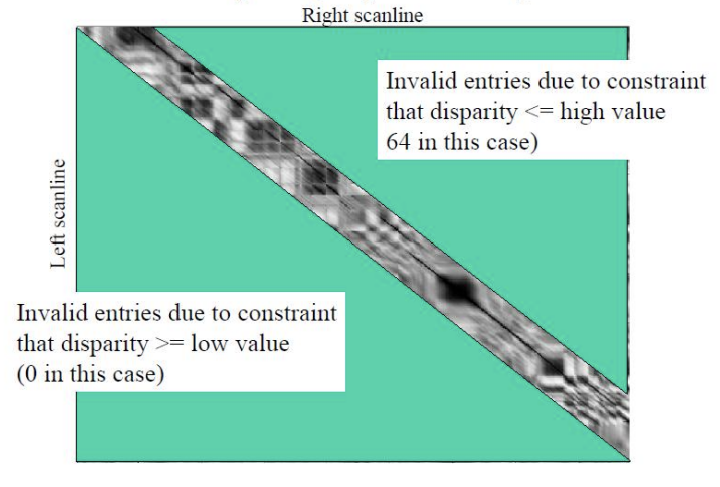
그런데, optimal path를 찾기 위해 DSI 전체를 다 봐야 할까(full-search)?
→ 그렇지 않다.
1. 두 이미지의 이동을 보고, 대각선 위 아래 중 버려도 되는 곳을 찾는다.
→ search할 영역이 반으로 줄어듦
2. baseline을 알고 있으므로, 대각선에서 어느 정도 떨어진 영역까지만 보면 된다.
→ 탐색할 영역이 또 부분적으로 줄어듦
DSI and Scanline Consistency

100x100 이미지라면, 두 이미지에서 하나의 row만 보므로, 100x100 DSI가 나올 것이다. 또한, 이미지를 full-search하면 DSI image가 100개 나올 것이다.
Lowest Cost Path

- "best" path를 찾고 싶다.
- lowest "cost"(path를 따라 dissimilarity를 sum한 값이 minimum인 path)를 찾고 싶다.
Constraints on Path
path는 double back하지 않음.
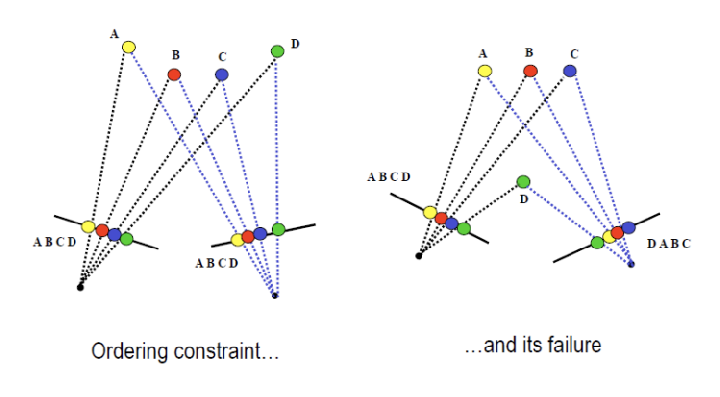
Ordering Constraints
Dealing with Occlusions
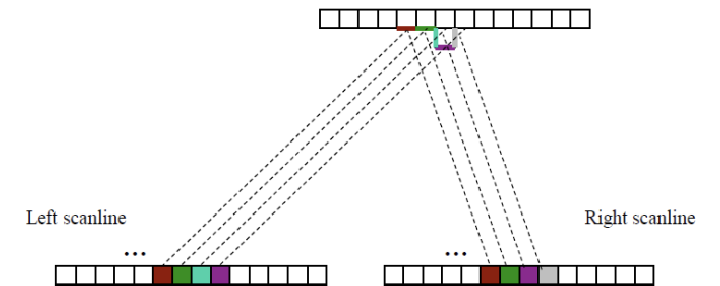
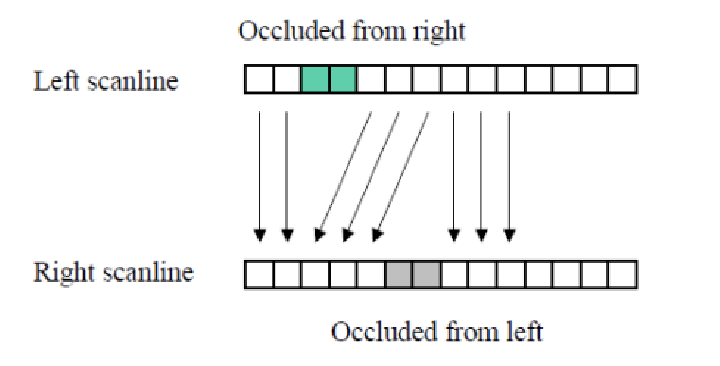
회색과 민트색같은 occlusion이 존재한다.
occlusion: 한 이미지에서는 보이는 영역이 다른 이미지에서는 안보이는 현상
Search Over Correspondences
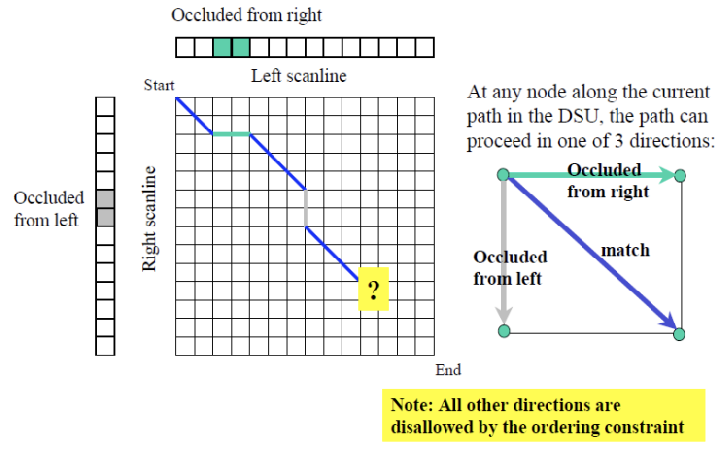
We have three cases
- Matching patches
- Occluded from right
- Occluded from left
- 민트 색은 right image에서만 보이는 영역이다.
- 회색은 left image에서만 보이는 영역이다.
ordering constraint를 고려하면, 위 세 가지 방향 이외의 방향은 불가능하다.
매 path를 결정할 때마다 dissimilarity에 따라 direction을 선택할 것이다(이 때, dissimilarity가 많이 높은 경우, left occlusion인지 right occlusion인지 결정해야 함)
- matching patches
- Cost = dissimilarity score
- Occluded from right
- Cost is some constant value
- Occluded from left
- Cost is some constant value
우리는 optimal path를 찾기 위해 Dynamic Programming 기법을 사용할 것이다.
full-search처럼 모든 path를 살필 필요는 없음. 그러나, DP는 모든 pixel의 가능성을 살핌.
Dynamic Programming은 내 픽셀에 올 때까지의 optimal한 score를 저장해둠. 실제로 path finding은 한 번 수행함. 모든 픽셀의 가능성을 보며 값을 저장해둘 뿐임.