📝 최대 공약수와 최소 공배수

문제 링크

📌 유클리드 호제법

• 두 자연수의 최대공약수를 구하는 알고리즘

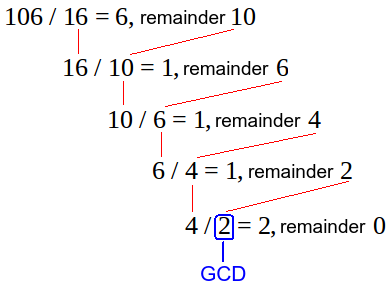
• a와 b(a > b)의 최대 공약수는, a와 b를 나눈 나머지인 r과 b의 최대 공약수와 같습니다.

• 이름에서 알 수 있듯이, a와 b를 나눈 나머지로 b를 나누고, 그렇게 나눈 나머지로 또 b를 나누고... 계속 이런 식으로 0이 될 때까지 숫자끼리 서로 나누는 방식입니다. (아래 이미지로 이해하면 훨씬 쉽습니다.😊 이미지 출처)

📌 최소 공배수

• 두 자연수 a와 b를 곱한 수를 최대 공약수로 나누면 최소 공배수라는 성질을 이용했습니다.

a = 4, b = 6

const k = gcd(a, b); // 최대 공약수: 2
const lcm = a * b / k; // 최소 공배수: 24 / 2 = 12

나의 풀이

• 따라서 저는 유클리드 호제법을 이용해 최대 공약수를 구하는 함수를 정의해 최대 공약수를 구하고, 구한 최대 공약수를 이용해 최소 공배수를 구했습니다.

function solution(n, m) {
    let a = Math.max(n,m);
    let b = Math.min(n,m);
    
    function gcd(a, b){
        let remainder;
      	// 나머지가 0이 될 때까지 반복
        while(b > 0) {
            remainder = a % b;
			// b를 remainder로 나누어야 하기 때문에,
      		// a % b의 a 자리에 b를 할당합니다.
            a = b;
			// b를 remainder로 나누어야 하기 때문에,
      		// a % b의 b 자리에 remainder를 할당합니다.
            b = remainder;
        }
        return b;
    }
    
    function lcm(a, b){
        let k = gcd(a, b);
        return (a * b) / k
    }
    
    return [gcd(a, b), lcm(a, b)]
}

다른 풀이

function gcdlcm(a, b) {
    var r;
    for(var ab= a*b; r = a % b; a = b, b = r){}
    return [b, ab/b];
}