Backpropagation

김당찬·2022년 3월 26일

Deep Learning

목록 보기

3/6

Backpropagation

이전에 최적화와 관련된 내용에서 살펴보았듯이, 어떤 머신러닝 모델을 최적화하는 기본적인 아이디어는 입력에 따른 출력의 변화, 즉 그래디언트를 계산하는 것에 있다. 그러나 딥러닝에서는 레이어와 노드의 수가 많아질수록 연결관계가 기하급수적으로 복잡해지고 이에 따라 하나의 가중치벡터(혹은 행렬)에 대한 그래디언트를 explicitly하게 구하기 어렵다. 따라서 이를 해결하기 위해 조금 더 계산적인computational 방법이 고안되었고, 이것이 무려 1985년에 고안된 역전파backpropagation 알고리즘이다(David E. Rumelhart et al.). 이번 글에서는 역전파의 기본적인 메커니즘과 이를 코드로 구현하는 방법을 살펴보도록 하자.

Basic backpropagation

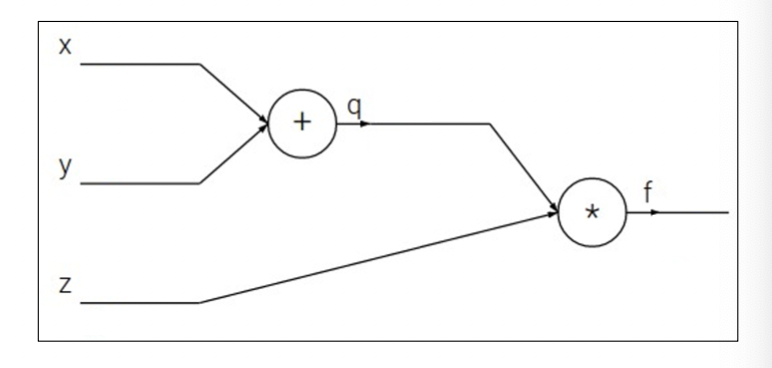
위와 같이 가장 간단한 형태의 네트워크를 생각하자. 위 네트워크는 3개의 입력값을 바탕으로 두 개의 노드 연산을 거쳐 출력값 $f(x,y,z)=(x+y)z$ 를 도출한다. 이때 $q(x,y)=x+y$ 를 첫번째 연산 노드로 하고 곱셈을 두번째 노드로 하자. 만일 데이터 $(x,y,z)=(-2,3,5)$ 가 주어졌다고 하자. 그러면 아주아주 간단한 연산으로 우리는 출력값 $f=5$ 와 중간출력값 $q=1$ 을 얻어낼 수 있다. 이렇게 입력받은 데이터로부터 순서대로 노드연산을 진행해 출력값을 얻는 것을 Forward pass라고 한다.

이때 각 입력변수 $x,y,z$ 에 대해 출력값(손실함수) $f$ 의 편미분계수를 구하려고 하자. 일반적으로는 $\partial f/\partial x$ 를 구하기 위해 $f$ 의 도함수 $df/dx=z$ 를 구하고 값을 대입하는 방법을 생각할 것이다. 그런데, 미분의 성질 중 하나인 Chain Rule연쇄법칙로부터

\frac{\partial f}{\partial x} = \frac{\partial q}{\partial y}\cdot\frac{\partial f}{\partial q}

의 관계식이 성립하므로, $x$ 에 대한 도함수를 구하지 않고도 이를 구할 수 있다. 이렇게 각 노드에 대한 그래디언트를 계산하며 역으로 입력변수에 대한 손실함수의 그래디언트를 구해나가는 과정을 Backward pass 라고 한다.

Up/Downstream Gradient

신경망의 한 노드 f에 대해 위와 같은 형태의 연결관계가 있다고 하자. 이때 이 노드는, 오른쪽으로는 신경망이 진행되며 출력값( $L\in\mathbb R$ , 손실함수값 )이 도출되고, 왼쪽으로는 입력 데이터가 처리되어 전해져오는 구조이다. 노드 f의 출력값 $z$ 와 손실함수값 $L$ 에 대해 구해지는 그래디언트 $\partial L/\partial z$ 을 Upstream gradient라고 한다. 마찬가지로, 노드의 입력값 $x,y$ 에 대해서 구해지는 그래디언트 $\partial L/\partial x, \partial L/\partial y$ 들을 Downstream gradient라고 한다. 반면, 노드 f의 연산자(ex. $z=x+y$ , $z=\max(x,y)$ )에 의해 발생하는 그래디언트 $\partial z/\partial x, \partial z/\partial y$ 들을 Local gradient라고 정의한다.

이때 연쇄법칙에 의해

\text{Downstream}=\text{Local}\times\text{Upstream}

의 관계가 성립한다. 이와 같은 방식으로 복잡한 신경망에서도 각 노드의 가중치들에 대한 그래디언트를 구할 수 있다. 이러한 방식을 역전파 알고리즘이라고 한다.

Multidimensional Case

앞서 설명한 역전파 알고리즘에서는 Input data $x,y$ 가 스칼라라는 가정을 생략했다. 이번에는 $x,y\in\mathbb R^d$ 인 경우, 즉 입력 데이터가 벡터로 주어지는 경우에 대해 생각해보자. 최종 출력값 $L$ 은 손실함수 값이므로 이는 변함없이 스칼라이다. 그러나 노드 $f$ 의(두 번째 그림 참조) 연산이 내적inner product 등의 형태가 아닌 이상 출력값 $z$ 역시 스칼라임은 보장할 수 없다. 따라서 $z$ 역시 벡터 형태일 수 있고, 이에 따라 Local gradient 역시 벡터 미분에 의해 자코비안Jacobian으로 주어진다❗️

그런데, Jacobian 행렬은 대부분의 경우 희소행렬sparse matrix이 되고, 이는 불필요한 연산비용을 초래한다. Input vector $x= \begin{pmatrix}1&3&-2&4\end{pmatrix}$ 의 각 성분에 대해 ReLU 연산을 수행하는 노드를 생각하자. 이때 이 노드의 input과 output $y$ 사이의 Jacobian을 구하면

\frac{dy}{dx}= \begin{pmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&0&0\\ 0&0&0&1 \end{pmatrix}

로, 애초에 ReLU 연산이 주어진 값을 그대로 반환하거나(미분계수 1) 음수를 clip하기 때문에, 대각성분이 1 또는 0인 대각행렬이 된다. 그런데 행렬연산은 같은 크기의 벡터 연산에 비해 제곱의 연산비용( $O(n^2)$ )을 소모하므로, 입력 및 출력 데이터 차원이 커질수록 자코비안을 처리하는 것은 매우 비효율적인 과정이 된다. 따라서 자코비안을 구해 행렬연산을 처리하는 대신 다음과 같은 논리연산을 이용해 효율적으로 처리하는 것이 낫다.