Expectation Propagation

김당찬·2023년 7월 14일

Expectation Propagation(EP) 알고리즘은 Laplace approximation에서 살펴본 것과 같이 사후확률분포를 근사하는 알고리즘 중 하나이다. 이번 글에서는 Expectation Propagation 알고리즘을 살펴보고 Gaussian Process에 어떻게 적용될 수 있는지와 Laplace approximation과 어떤 성능 차이를 보이는지를 살펴보고자 한다.

Expectation Propagation

베이즈 정리에 의해, 사후확률분포는 사전분포와 가능도함수의 곱에 비례한다. 이때, 사후확률분포의 적분값을 1로 만들기 위해 normalizing constant $Z$ 를 나누어주기도 하는데, 나누어주지 않은 경우 이를 unnormalized density(아래)라고도 한다.

p(\theta|y) = p(\theta) \times p(y|\theta)

만약 위 경우가 $n$ 개의 데이터셋이 주어진 상황이라면, 가능도함수를 다음과 같이 개별 데이터에서의 marginal likelihood의 곱으로 표현가능하다.

p(y|\theta) = \prod_{i=1}^{n}p(y_{i}|\theta) =:\prod_{i=1}^{n}f_{i}(\theta)

회귀분석의 경우에는 대체로 marginal likelihood의 정규분포가 가정되므로, 문제가 없지만 분류문제의 경우 $f_{i}$ 를 정규분포로 가정할 수 없는 경우가 많다. 따라서 사후확률분포를 구하는 것 역시 까다로워진다. 이를 극복하기 위해, $f_{i}$ 들을 보다 추정이 쉬운 $g_{i}$ 들로 각각 근사하는 방법을 이용하는데, 이를 Expectation propagation이라고 한다.

\prod_{i=1}^{n}f_{i}(\theta)\simeq\prod_{i=1}^{n}g_{i}(\theta)

일반적으로, $g$ 는 지수족(exponential family)을 이용하는데, 대부분의 경우 정규분포를 사용한다. 또한, 표기의 편의상 $\theta$ 의 사전분포를 $f_0,g_0$ 으로 두고 다음과 같이 표기한다.

p(\theta|y)=\prod_{i=0}^{n}f_{i}(\theta)\simeq\prod_{i=0}^{n}g_{i}(\theta) =: g(\theta)

Algorithm

EP algorithm은 단계별로 근사분포 $g_{i}$ 들을 계속 업데이트하는 과정으로 진행된다.
1. 우선 각 반복 과정에서 $i$ 번째 데이터에 대해 다음과 같은 두 가지 분포가 정의된다.

\begin{aligned} &g_{-i}(\theta)= \frac{g(\theta)}{g_{i}(\theta)} \quad(\text{cavity distribution})\\ &t_{i}(\theta)= g_{-i}(\theta)f_{i}(\theta)\quad(\text{tilted distribution}) \end{aligned}

tilted distribution에 대한 근사분포를 구하여 $g(\theta)$ 를 업데이트한다. 이때 근사 방법은 moment-matching approach(평균, 분산을 같도록 방정식을 푸는 것)을 사용한다.

Moment matching approach를 이용해 구한 근사분포는 대상 분포와 Kullback-Leibler divergence가 가장 작은 분포가 된다.

예를 들면, $g(\theta)$ 가 정규분포 $N(\theta|\mu,\Sigma)$ 를 따른다고 가정할 때 moment matching은 다음과 같이 이루어진다.

\begin{aligned} \mu &= \mathrm{E}[t_{i}(\theta)]=\int\theta g_{-i}(\theta)f_{i}(\theta)d\theta\\ \Sigma&= \mathrm{Var}(t_{i}(\theta))=\int(\theta-\mu)(\theta-\mu)^{T}g_{-i}(\theta) f_{i}(\theta)d\theta \end{aligned}

과정 1-2를 거쳐 각 step마다 $g$ 를 업데이트 하거나(sequential EP) 혹은 전체 데이터셋에 대해 tilted moment를 구한 후 업데이트를 하여(Parallel EP) 사후확률분포를 계산할 수 있다.

Example. Gaussian Process Binary Classification

Data : 설명변수 1개(1차원), 2개 클래스 분류

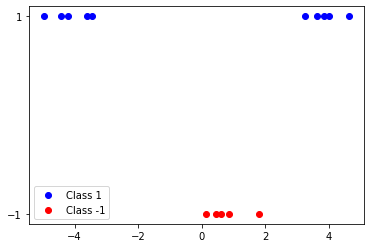
EP 알고리즘을 실행하기 위한 코드는 다음과 같다.

# Define Expectation Propagation
from copy import deepcopy

def EP(K, y, max_iter=100):
    # Initialize
    N = len(y)
    nu = np.zeros(N) # cavity parameters
    tau = np.zeros(N)
    mu = np.zeros(N) # posterior parameters
    Sigma = deepcopy(K)  

    for _ in range(max_iter):
        for i in range(N):
            # Approximate cavity dist parameters
            cavity_mean = 1/K[i,i] * mu[i] - nu[i]
            cavity_var_inv = 1/K[i,i] - tau[i]
            cavity_var = 1/cavity_var_inv

            # marginal moments
            z_i = y[i] * cavity_mean / np.sqrt(1 + cavity_var)
            marginal_mean = cavity_mean + ((y[i] * cavity_var * norm.pdf(z_i)) / (norm.cdf(z_i) * np.sqrt(1 + cavity_var)))
            marginal_var = cavity_var - ((cavity_var**2 * norm.pdf(z_i)) / (norm.cdf(z_i) * (1 + cavity_var))) * (z_i + norm.pdf(z_i)/norm.cdf(z_i))

            # Update Site Parameters
            delta_tau = (1 / marginal_var) - cavity_var_inv - tau[i]
            tau[i] += delta_tau
            nu[i] = marginal_mean / marginal_var - cavity_mean

            # Update Posterior Parameters
            s_i = Sigma[:,i]
            Sigma = Sigma - (1 / (1/delta_tau + Sigma[i,i])) * np.outer(s_i, s_i)
            mu = Sigma @ nu

        # Recompute approximate posterior
        S = np.diag(tau)
        S_sqrt = np.sqrt(S)
        L = np.linalg.cholesky(np.eye(N) + S_sqrt @ K @ S_sqrt)
        V = np.linalg.solve(L.T, S_sqrt @ K)
        Sigma = K - V.T @ V
        mu = Sigma @ nu

    
    return nu, tau # natural site parameters

def predict_EP(X, y, nu, tau, x_new, kernel):
    N = len(y)
    K = cov_matrix(X, kernel)
    S = np.diag(tau)
    S_sqrt = np.sqrt(S)
    L = np.linalg.cholesky(np.eye(N) + S_sqrt @ K @ S_sqrt)
    z = np.linalg.solve(S_sqrt @ L.T, np.linalg.solve(L, S_sqrt @ K @ nu))
    kernel_vec = np.array([kernel(x_new, X[i]) for i in range(N)])
    mean_new = np.inner(z- nu, kernel_vec)
    v = np.linalg.solve(L, S_sqrt @ kernel_vec)
    var_new = kernel(x_new, x_new) - np.inner(v,v)

    pi_new = norm.cdf(mean_new / np.sqrt(1 + var_new))

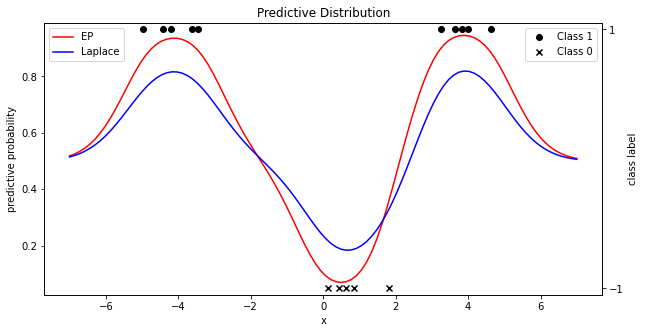
    return mean_new, var_new, pi_new

여기서 cavity_var은 $\tau_{-i}=\sigma_{-i}^{-2}$ 를 의미하는데, 계산의 편의성을 위해 사용한다. 또한, 전체 스텝 진행 후 업데이트하는 Parallel EP 대신 Sequential EP를 사용했다(교재 참고). 위 코드와 데이터로 예측확률분포(predictive probability distribution)을 다음과 같이 구하였는데, 이전에 살펴본 Laplace approximation과 결과를 비교했다.

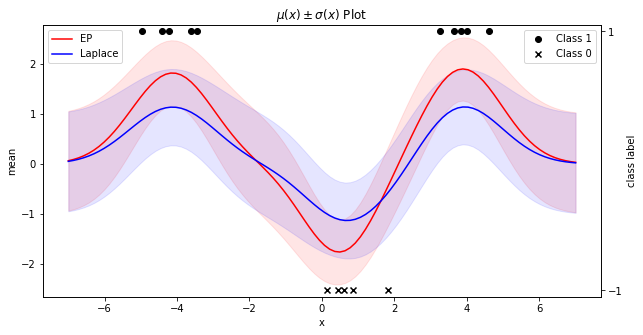
또한, Mean function $\bar f(x)$ 는 다음과 같다. Mean function 위 아래로 칠해진 영역은 $\pm$ 표준편차 만큼의 영역을 의미한다.

References

Gelman - Bayesian Data Analysis
Gaussian Process for Machine Learning
Code on Github : https://github.com/ddangchani/Velog/blob/main/Statistical%20Learning/GP%20binary_EP.ipynb

김당찬

블로그 이사했습니다 https://ddangchani.github.io

이전 포스트

Expectation Propagation