Support Vector Regression

김당찬·2022년 5월 24일

Support Vector Regression

이전 게시글에서 SVM의 작동 원리와 SVR, 즉 support vector regression이 SVM의 원리를 차용하여 생성되는 모델이라는 점에 대해 살펴보았다. 이번에는 paper "A Tutorial on Support Vector Regression(2003)"을 바탕으로 SVM이 회귀분석에 사용되는 경우만 특히 집중해서 살펴보고, 이와 더불어 사용되는 NuSVR 모델에 대해서도 간략히 다루어보도록 하자.

SVR

이전에 살펴본 내용에서 $\epsilon$ -insensitive error measure $V_\epsilon(r)$ 을 이용한 방법을 다루었다. 이를 $\epsilon$ -SVR 이라고도 하며, primal (optimization) problem은 다음과 같이 주어진다[Vapnik, 1995].

\min_{w,b,\xi,\xi^*} {1\over2}\Vert w\Vert^2 + C\sum_{i=1}^N(\xi_i+\xi_i^*)\\ \text{subject to}\\ y_i-\langle w,\phi(x_i)\rangle-b\leq\epsilon+\xi_i,\\ \langle w,\phi(x_i)\rangle+b-y_i\leq\epsilon+\xi_i^*,\\ \xi_i,\xi_i^*\geq 0,\\ i=1,\ldots,N \tag{1}

Induction

함수 $f(x) = \langle w, x\rangle + b$ 를 추정하기 위해 Risk functional(위험 범함수)
$R[f] = \int_\mathcal X L(f,x,y) dP(x,y)$
을 최소화하는 함수 $f$ 를 찾는 과정을 생각하자. 이때 Input space $\mathcal X$ 에서의 확률분포 $P(x,y)$ 는 알 수 없으므로, empirical risk를 사용하게 되고 이 과정에서 $\epsilon$ -insensitive loss function(아래 내용 참고)을 이용하여 다음과 같다.
$R_\text{emp}[f]:={1\over N}\sum_{i=1}^N|y-f(x_i)|_\epsilon$
Empirical risk를 이용해 다음과 같이 regularized risk functional
${1\over2}\Vert w\Vert^2 + C\cdot R_\text{emp}[f]$
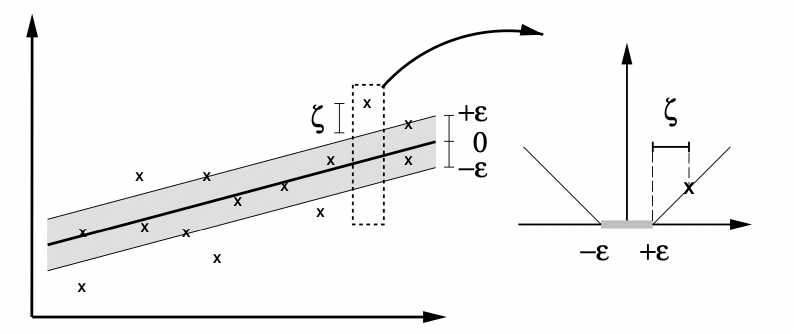
을 최소화하는 $f$ 를 찾는 문제는 결국 식 (1)와 동일한 최적화문제로 귀결된다( $\epsilon$ 미만의 오차를 용인하는 것을 slack variable $\xi$ 를 이용해 표현한 것이다. 아래 그림 참고).

여기서 상수 $C>0$ 은 hyperplane $f$ 의 flatness와 $\epsilon$ 이상의 오차를 얼마만큼 용인(tolerate)할지에 대한 trade-off 이다. $\xi_i,\xi_i^*$ 는 margin과 관련된 penalize 변수이며, $\phi(x)$ 는 각 feature transformation을 의미한다. 제약조건의 앞선 두 식을 살펴보면, 실제 관측값 $y_i$ 와 추정값 $w^T\phi(x_i)+b$ 의 오차가 최소 $\epsilon$ 보다는 큰 관측 샘플들에 대해 penalize variable $\xi_i$ 를 부과한다. 즉, 오차가 $\epsilon$ 보다 작은 관측값에 대해서는 penalizing이 이루어지지 않으며, 이는 이전 게시글에서 언급한 $\epsilon$ -insensitive과 일맥상통한다. $\epsilon$ -sensitive loss function은

|\xi|_\epsilon = \max(0,|\xi|-\epsilon)

으로 쓸 수 있으며, 실제 관측값 $y_i$ 로부터 $\epsilon$ 만큼의 범위를 $\epsilon$ -tube 라고도 한다(아래 그림의 회색 영역).

앞선 최적화문제 식 (1)은 dual formulation을 이용하여 쉽게 해결할 수 있는데, Lagrange multipliers 방법을 이용하여 다음과 같이 유도할 수 있다.

Dual Problem of SVR

우선 primal objective function을 다음과 같이 Lagrangrian $L$ , Lagrange multipliers $\alpha_i,\alpha_i^*,\eta_i,\eta_i^*$ 를 이용해 다음과 같이 나타내도록 하자.

L := {1\over2}\Vert w\Vert^2 + C\sum_{i=1}^N(\xi_i+\xi_i^*)-\sum_{i=1}^N(\eta_i\xi_i + \eta_i^*\xi_i^*) - \sum_{i=1}^N\alpha_i(\epsilon+\xi_i-y_i+\langle w,x_i\rangle +b) - \sum_{i=1}^N\alpha_i^*(\epsilon+\xi_i^*+y_i - \langle w, x_i\rangle-b)\tag{2}

편의상 $\alpha_i^{(*)}, \eta_i^{(*)}$ 가 각각 $\alpha_i,\alpha^*_i$ 와 $\eta_i,\eta_i^*$ 에 모두 대응된다고 하자. 그러면 dual variable로 주어지는 $\alpha_i^{(*)},\eta_i^{(*)}$ 는 모두 0 이상의 값을 가져야 한다. 또한, primal problem(식 1)의 변수 $(w,b,\xi_i,\xi_i^*)$ 에 대해 안장점 조건, 즉 각 변수들에 대한 $L$ 의 편미분계수가 0으로 소멸(vanish) 되어야 하므로

\partial_bL = \sum_{i=1}^N(\alpha^*_i-\alpha_i) = 0 \\ \partial_wL = w - \sum_{i=1}^N(\alpha_i-\alpha_i^*)x_i = 0\\ \partial_{\xi_i^{(*)}}L = C-\alpha_i^{(*)} - \eta_i^{(*)}\tag{3}

와 같은 세 개의 조건을 얻는다. 위 세 조건 (3)를 primal objective function 식 (2)에 대입하여 정리하면 다음과 같은 dual optimization problem을 얻는다(함수 $W(\alpha,\alpha^*)$ 의 최대화 문제).

W(\alpha,\alpha^*)= -{1\over2}\sum_{i,j=1}^N(\alpha_i-\alpha_i^*)(\alpha_j-\alpha_j^*)\langle x_i,x_j\rangle -\epsilon\sum_{i=1}^N(\alpha_i+\alpha_i^*)+\sum_{i=1}^Ny_i(\alpha_i-\alpha_i^*) \\ \text{subject to}\\ \sum_{i=1}^N(\alpha_i-\alpha^*_i) = 0 \;\;\text{and}\;\; \alpha_i^{(*)}\in[0,C]

이 과정에서 $\eta_i^{(*)}$ 는 조건 (3)의 세번째 식으로부터 소거되었음을 확인할 수 있다. 또한, 조건 (3)의 두번째 식으로부터

w = \sum_i(\alpha_i-\alpha_i^*)x_i

를 얻을 수 있는데, 이를 이용해 hyperplane function $f(x)$ 를

f(x)= \sum_i(\alpha_i-\alpha_i^*)\langle x_i,x\rangle + b\tag{4}

와 같은 형태로 쓸 수 있다. 이를 Support Vector expansion 이라고 하는데, 이 과정에서 hyperplane의 parameter $w$ 가 오로지 관측 데이터 $x_i$ 와 관련된 training pattern들의 선형결합으로 나타나는 사실을 확인할 수 있다. 즉 함수 $f$ 를 계산하는 과정은 Input space의 차원과 무관하게, support vector들의 개수에만 의존한다는 사실이다.

이러한 dual representation에서의 핵심은 식 (4)에서 특성공간의 내적 $\langle x_i,x\rangle = \phi(x_i)^T \phi(x)$ 대신 커널 함수 $k(x,x')$ 를 적용하면(Kernel Trick) 기존의 hyperplane function $f$ 대신

f(x) = \sum_i(\alpha_i-\alpha_i^*)k(x_i,x) +b

의 형태를 사용할 수 있다. 커널함수의 조건에 관련된 자세한 정리들은 여기서 생략하도록 하겠다.

LinearSVR

Primal problem

\min_{w,b,\xi,\xi^*} {1\over2}\Vert w\Vert^2 + C\sum_{i=1}^N(\xi_i+\xi_i^*)\\

에서 Loss 부분은 $\sum_i(\xi_i+\xi_i^*)$ 를 의미한다. 이때 classification 문제의 hinge loss와 유사한 epsilon-insensitive loss 를 이용하면 다음과 같은 primal problem

\min_{w,b} {1\over 2}\Vert w\Vert^2 + C\sum_i\max(0, |y_i-\langle w,\phi(x_i)\rangle + b| -\epsilon)

을 얻는데, 이를 최적화문제로 삼아 풀면 Linear Support Vector Regressor 모델을 얻을 수 있다.

NuSVR

NuSVR(Nu는 그리스 소문자 $\nu$ 를 의미한다) 알고리즘은 앞서 살펴본 $\epsilon$ -SVR의 메커니즘과 유사하지만 $\epsilon$ 값을 사전에 설정하는 $\epsilon$ -SVR과 다르게 $\epsilon$ 의 크기를 또 다른 상수 $\nu\geq 0$ 를 이용해 제어한다. 우선 primal problem은 다음과 같이 주어진다.

\min \tau(w,\xi^{(*)},\epsilon) = {1\over2}\Vert w\Vert^2 + C\cdot\bigl( \nu\epsilon + {1\over N}\sum_{i=1}^N(\xi_i+\xi_i^*) \bigr)\tag{5} \\ \text{subject to}\\ \langle w,x_i\rangle + b - y_i \leq \epsilon + \xi_i\\ y_i - (\langle w, x_i\rangle + b) \leq \epsilon + \xi_i^* \\ \xi_i^{(*)}\geq 0, \epsilon \geq 0

제약조건들에 대해 Lagrange multipliers $\alpha_i^{(*)}, \eta_i^{(*)},\beta\geq 0$ 을 설정하여 다음과 같은 Lagrangrian

\begin{aligned} L(w,b,\alpha^{(*)},\beta,\xi^{(*)},\epsilon,\eta^{(*)}) = &{1\over 2}\Vert w\Vert^2 + C\nu\epsilon + {C\over N}\sum_i(\xi_i+\xi_i^*)-\beta\epsilon - \sum_i(\eta_i\xi_i+\eta_i^*\xi_i^*)\\ &-\sum_i\alpha_i(\xi_i+y_i-\langle w,x_i\rangle - b +\epsilon)\\ &-\sum_i\alpha_i^*(\xi_i^*+\langle w,x_i\rangle + b -y_i+\epsilon) \end{aligned}

을 얻을 수 있다. 또한, 식 (5)를 최적화하기 위해 primal variable에 대한 lagrangrian의 편미분계수를 0으로 하는 다음 방정식들을 구하자.

w = \sum_i(\alpha_i^*-\alpha_i)x_i \\ C\nu - \sum_i(\alpha_i + \alpha_i^*) -\beta =0 \\ \sum_{i=1}^N(\alpha_i - \alpha_i^*) = 0 \\ {C\over N}-\alpha_i^{(*)}-\eta_i^{(*)} = 0

SVR에서와 마찬가지로, 위 네개의 식 중 첫번째 식을 SV expansion(Support Vector expansion)이라고 정의하며, 이때 식 (5)의 첫번째 및 두번째 제약조건을 등식으로(=) 만족하는 관측값(i)들에 대해서만 $\alpha_i^{(*)}$ 값이 0이 아닌 값을 갖게 된다. 마찬가지로 이러한 관측값들을 support vector로 정의한다. 앞선 네 제약조건을 Lagrangrian $L$ 에 대입하면 새로운 optimization 문제를 얻는데, 이를 Wolfe dual problem이라고 한다. 이때, 최적화 문제의 내적을 커널 $k(x,y) := \langle \phi(x),\phi(y)\rangle$ 로 대체하면 위의 dual problem을 다음과 같은 새로운 형태로 쓸 수 있으며, 이 과정에서 dual varaible $\beta,\eta_i^{(*)}\geq 0$ 은 등장하지 않게 된다.

NuSVR Optimization Problem
$\max W(\alpha^{(*)}) = \sum_{i=1}^N(\alpha_i^{(*)} - \alpha_i)y_i - {1\over2}\sum_{i,j=1}^N(\alpha_i^*-\alpha_i)(\alpha_j^*-\alpha_j) k(x_i,x_j)$
$\begin{aligned}\text{subject to}\quad &\sum_{i=1}^N(\alpha_i-\alpha_i^*)=0 \\ &\alpha_i^{(*)}\in[0,{C\over N}] \\ &\sum_{i=1}^N(\alpha_i+\alpha_i^*) \leq C\cdot\nu \end{aligned}$

위 NuSVR optimization 문제의 regression estimate는 다음과 같은 형태를 취하게 된다.

f(x) = \sum_{i=1}^N(\alpha_i^*-\alpha_i)k(x_i,x) + b

여기서 상수 $b$ 와 primal optimization function의 $\epsilon$ 은 support vector 관측값들로부터 계산할 수 있게 된다.
NuSVR에서 $\nu$ 의 역할에 대해서 살펴보도록 하자. 만일 $\nu>1$ 이면, primal function에서 $C\nu\epsilon$ 항의 최소화로 인해 $\epsilon=0$ 이 도출된다. 반면 $\nu\leq 1$ 인 경우 만일 데이터가 noise-free하고 low-capacity model에 의해 interpolate될 수 있는 경우(여기서 interpolation은 모델이 관측 데이터들의 점을 모두 지나는 경우를 의미한다) $\epsilon = 0$ 인 경우가 발생할 수 있다. 그러나, 이는 plain L1-loss regression에 대응되므로, 이를 살펴보는 것은 큰 의미가 없게 된다.
다음 게시글에서는 NuSVR에서 parameter $\nu$ 의 수학적 의미와 이론적 중요성에 대해 자세히 살펴보도록 하자.

References

A Tutorial on Support Vector Regression, A.J. Smola, Bernhard Scholkopf. (2003).
New Support Vector Algorithm, B.Scholkopf et al. (2000).
Scikit-learn official document : https://scikit-learn.org/stable/modules/svm.html#svm-implementation-details

김당찬

블로그 이사했습니다 https://ddangchani.github.io

이전 포스트

모델 성능 개선만이 전부일까

다음 포스트

Support Vector Regression