따릉이 데이터 분석하기 (1) EDA
이번 시리즈는 공공데이터인 서울시 공유자전거 따릉이의 데이터를 이용한 small project를 진행해보고자 한다. 데이터를 비롯한 프로젝트의 내용은 데이콘의 내용을 바탕으로 진행했으며, 원래 주제는 데이터를 바탕으로 한 AI 모델을 개발하는 것이다. 하지만 여기서는 AI모델을 개발하기 전에, 회귀문제로 얼마나 높은 성능까지 끌어올릴 수 있는지를 먼저 파악해보고, 이를 바탕으로 다른 머신러닝/딥러닝 기법을 적용해보도록 하겠다.
Problem
이번 프로젝트의 문제는 다음과 같이 정의된다.
Type : Regression
Response Variable : 따릉이 대여 수(count, integer)
Predictor Variables
- Hour : 시간, 0부터 23까지의 integer
- 날씨 변수 : temperature, precipitation(0/1), windspeed, humidity, visibility, ozone, pm-10, pm-2.5
Metric : Root Mean Squared Error(RMSE)
Data Load & Descriptive Statistic
프로젝트의 데이터는 위 데이콘 페이지에서 받을 수 있으며, 우선 훈련에 사용되어야 하는 train.csv를 불러오도록 하자. 이는 pandas의 read_csv 를 이용해 작업 디렉토리의 데이터를 쉽게 불러올 수 있다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df_train = pd.read_csv('train.csv')또한, 모델링을 위해 predictor와 response variable을 분리해야 하는데, 이를 위해 위 데이터프레임을 아래와 같이 인덱싱했다.
X_train = df_train.iloc[:,1:10] # predictor variable
y_train = df_train.iloc[:,10] # response variable이후, 먼저 predictor variables의 기술통계량(descriptive statistics)을 파악해 데이터의 형태를 대략적으로 살펴보았다(아래 표와 같은 결과가 나왔다).
X_train.describe().round(1)| hour | hour_bef_temperature | hour_bef_precipitation | hour_bef_windspeed | hour_bef_humidity | hour_bef_visibility | hour_bef_ozone | hour_bef_pm10 | hour_bef_pm2.5 | |
|---|---|---|---|---|---|---|---|---|---|
| count | 1459.0 | 1457.0 | 1457.0 | 1450.0 | 1457.0 | 1457.0 | 1383.0 | 1369.0 | 1342.0 |
| mean | 11.5 | 16.7 | 0.0 | 2.5 | 52.2 | 1405.2 | 0.0 | 57.2 | 30.3 |
| std | 6.9 | 5.2 | 0.2 | 1.4 | 20.4 | 583.1 | 0.0 | 31.8 | 14.7 |
| min | 0.0 | 3.1 | 0.0 | 0.0 | 7.0 | 78.0 | 0.0 | 9.0 | 8.0 |
| 25% | 5.5 | 12.8 | 0.0 | 1.4 | 36.0 | 879.0 | 0.0 | 36.0 | 20.0 |
| 50% | 11.0 | 16.6 | 0.0 | 2.3 | 51.0 | 1577.0 | 0.0 | 51.0 | 26.0 |
| 75% | 17.5 | 20.1 | 0.0 | 3.4 | 69.0 | 1994.0 | 0.1 | 69.0 | 37.0 |
| max | 23.0 | 30.0 | 1.0 | 8.0 | 99.0 | 2000.0 | 0.1 | 269.0 | 90.0 |
pd.DataFrame의 describe() 메서드를 이용하면 위 표처럼 평균, 표준편차, 사분위수 등을 포함한 기술통계를 얻을 수 있다. hour의 경우 시간을 나타내므로 1열은 의미없는 데이터이고, 나머지 데이터를 위주로 살펴보면 될 것이다.
Bar Chart of Response variable
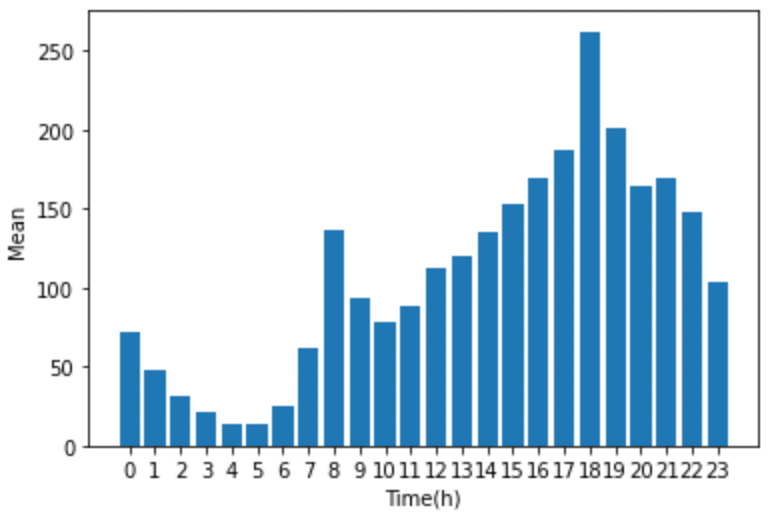
다음으로 반응변수인 따릉이 이용 대수(count)의 분포를 확인하기 위해 기본적인 bar chart를 이용해보도록 하자. 여기서는 X의 변수 중 시간(hour) 별 이용 대수를 아래 코드를 통해 plot으로 나타냈고, 결과는 아래 그림과 같다. 이용 대수가 시간별로 일정하지 않고, 오후 6시를 기점으로 편중된 분포를 가짐을 확인할 수 있다.
count_by_hour = pd.DataFrame({'hour' : X_train.iloc[:,0],
'count' : y_train})
mean = count_by_hour.groupby('hour').mean().round(1).reset_index()
plt.bar(range(len(mean)),mean['count'])
plt.xticks(range(len(mean)), mean['hour'])
plt.ylabel('Mean')
plt.xlabel('Time(h)')
plt.show()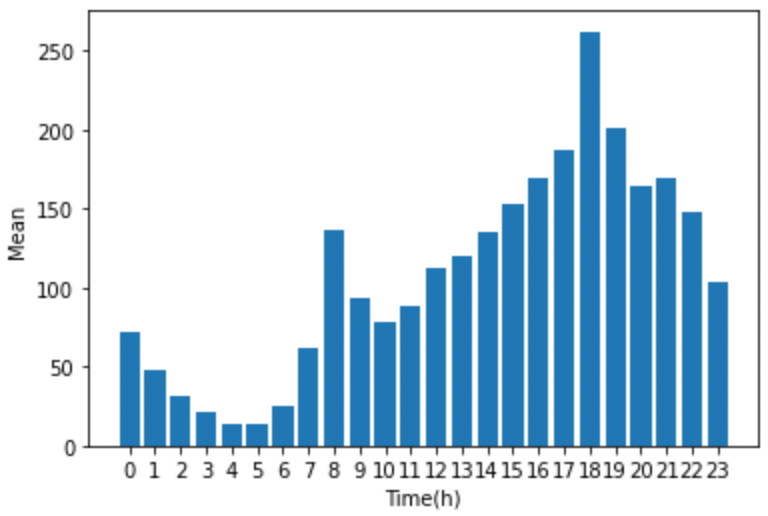
Correlation Check
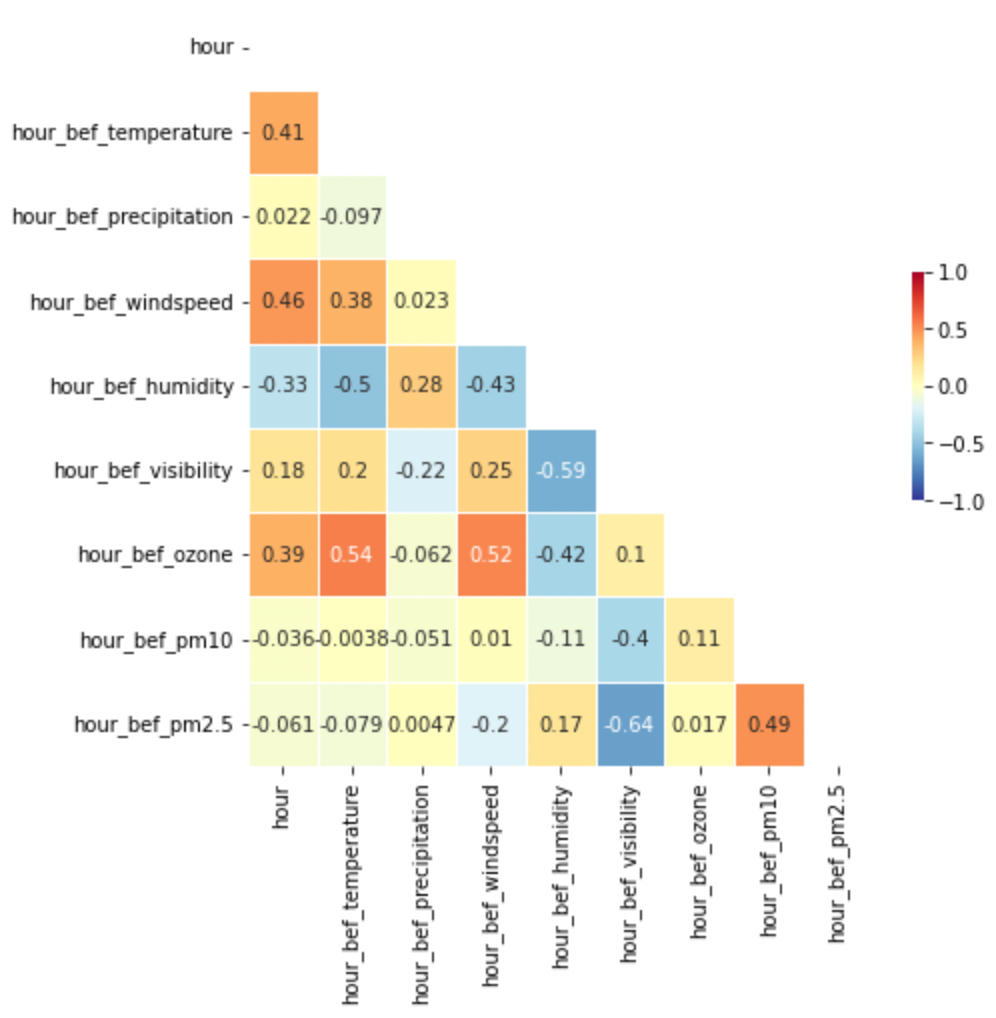
Regression 문제에서 가장 중요하다고 해도 과언이 아닌 것은, 바로 변수 간의 상관관계를 체크하는 것이다. Regession이란 것은 결국 각 변수들에 대응하는 최적의 가중치를 구해, 이것을 바탕으로 결과값을 예측하는 것인데 어떤 변수들 간의 상관관계가 존재한다면 이는 가중치의 추정을 어렵게 하고, 모델의 성능 역시 저하시킨다. 따릉이 데이터를 대강 살펴봐도, 미세먼지 농도를 나타내는 pm10, pm2.5 등의 변수와 가시거리를 나타내는 visibility 변수가 혼재하고 있다. 미세먼지 농도가 짙을 수록 가시거리가 낮은 것은 상식적인 현상이므로, 이들 사이에는 상관관계가 존재할 것이라는 합리적인 추정을 할 수 있다.
우선 다음과 같이 상관관계 표를 만들어보도록 하자.
fig, ax = plt.subplots(figsize=(7,7))
corr = X_train.corr()
mask = np.zeros_like(corr, dtype = np.bool_)
mask[np.triu_indices_from(mask)] = True
sns.heatmap(corr, mask = mask,
annot = True, linewidth=.5,
cmap = 'RdYlBu_r', cbar_kws = {"shrink": .3}, # shrink cbar(cmap)
vmin = -1, vmax = 1)
plt.show()위 코드는 아래와 같은 heatmap plot을 나타내주는 코드로, 이는 변수 간 상관관계를 pd.DataFrame.corr() 메서드를 통해 구한 것을 시각화해준다. 빨간색(+1.0)과 파란색(-1.0)에 가까워질수록 각각 두 변수가 양/음의 상관관계를 강하게 갖는 것을 의미하는데, 앞서 말한 것 처럼 pm2.5와 visibility가 가장 강력한 -0.64의 표본상관계수를 갖는다.