[알고리즘] 분할 정복(divide & conquer)

분할 정복이란?

• 분할 정복이란 유명한 알고리즘 디자인 패러다임으로, 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 재귀 호출을 이용해 계산하고, 각 부분 문제의 답으로 전체 문제의 답을 계산해내는 방법이다.
• 분할 정복 알고리즘은 크게 아래 세가지 구성요소를 가진다.

1. 문제를 더 작은 문제로 분할하는 과정(divide)
2. 각 문제에 대한 답을 원래 문제에 대한 답으로 병합하는 과정(merge)
3. 더이상 답을 분할하지 않고 곧장 풀 수 있는 매우 작은 문제(base case)

분할 정복 예시와 문제점

행렬의 거듭제곱

• n x n 행렬A가 주어질때, A^m은 A를 연속해서 m번 곱한 것이다.
• 단순히 m번 곱하는 알고리즘으로 설계하면 O(n^3m)의 시간이 걸리기 때문에 계산에 어려움이 있다. (가장 단순한 행렬곱 알고리즘을 이용하면 O(n^3)이 걸린다.
• 이러한 문제를 분할정복을 이용하면 빠르게 값을 구할 수 있게 된다.

행렬 거듭제곱을 구하는 분할 정복 알고리즘

• A^m = A^m/2 X A^m/2 를 이용하여 설계한 알고리즘은 다음과 같다.

//정방행렬을 표현하는 클래스
class SquareMatrix;
//n*n크기의 항등 행렬을 반환하는 함수
SquareMatrix identity(int n);
//A^m 반환
SquareMatrix pow(SquareMatrix A, int m) {
   if (m == 0 ) return identity(A.size());
   if (m % 2 > 0 ) return pow(A, m-1) * A;
   SquareMatrix half = pow(A, m / 2);
   return half * half;
}

다른 방식으로 분할했을 때 발생하는 문제점

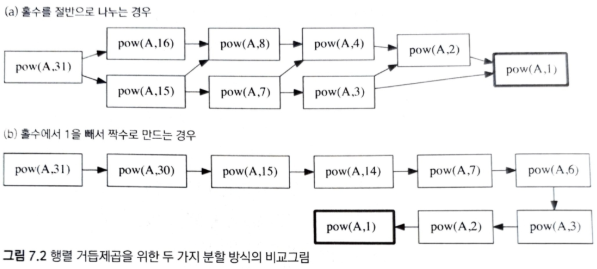
• 위 그림에서 우리는 b의 방식으로 알고리즘을 설계하여 부분 문제들의 중복이 발생하지 않았다.
• 하지만 A방식으로 설계했다면? 위 그림에서 pow(A,8), pow(A,4) 처럼 여러 하위 문제들이 중복되어 계산되기 때문에 성능을 크게 떨어뜨린다.
• 이러한 중복 문제를 해결하기 위해 동적 계획법 Memoization 방식이 고안되었다.