[논문 리뷰] CatBoost: unbiased boosting with categorical features

https://arxiv.org/pdf/1706.09516

Abstract

새로운 그래디언트 부스팅 툴킷인 CatBoost의 핵심 알고리즘 기술을 소개한다. CatBoost는 1) 'ordered boosting'이라는 순열 기반 부스팅 방식과 2) 범주형 특성 처리를 위한 혁신적인 알고리즘을 통해 기존의 그래디언트 부스팅 방식에서 발생하는 타겟 누수 문제를 해결하고, 다양한 데이터셋에서 다른 부스팅 구현체보다 우수한 성능을 보인다. 이 논문은 이러한 문제와 알고리즘의 효과적인 해결 방법을 분석하고 결과를 제시하여 CatBoost의 효과를 입증한다.

Introduction

Gradient boosting의 기존 구현들이 특정 통계적 문제에 직면하고 있다. 이 문제는 모델이 훈련 예제의 대상에 의존하여 테스트 예제의 예측에 영향을 미치는 것으로 나타났다. 이로 인해 모델의 예측이 왜곡되는 현상이 발생하며, 범주형 특성을 처리할 때도 비슷한 문제가 발생한다. 이러한 문제를 해결하기 위해 정렬 원칙에 기반한 ordered boosting과 범주형 기능을 처리하기 위한 새로운 알고리즘을 제안한다.

Background

주어진 데이터셋 D는 m개의 특성으로 이루어진 무작위 벡터 xk와 목표값 yk로 구성된다. 여기서 목표값은 이진 또는 숫자적 응답일 수 있다. 목표는 함수 F : Rm → R을 학습하여 예상 손실을 최소화하는 것이다.

경사 부스팅 절차는 그리디 방식으로 순차적인 근사치인 Ft: Rm→R의 시퀀스를 구축한다. Ft는 이전 근사치인 Ft-1에 추가적인 예측을 더하여 얻어진다. 기울기 하강법을 사용하여 손실을 최소화하는 기능 ht를 선택하며, ht는 gt(xy)를 근사하도록 선택된다. CatBoost는 이러한 경사 부스팅의 구현 중 하나로, 이진 결정 트리를 기본 예측기로 사용한다. 결정 트리는 특성 공간을 재귀적으로 분할하여 모델을 구축하며, 각 영역에는 해당 영역에서의 응답 값을 나타내는 값이 할당

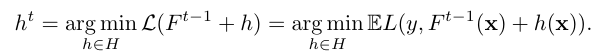
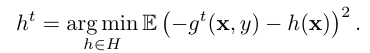
Categorial features

Related work on categorical features

카테고리 특성은 비교할 수 없는 카테고리라는 이산값 집합을 가지는 특성이다. 원-핫 인코딩을 사용하는 경우 고차원 특성에서 많은 새로운 특성을 생성하는 문제가 있다. 이 문제를 해결하기 위해 카테고리를 제한된 수의 클러스터로 그룹화하고 그런 다음 원-핫 인코딩을 적용할 수 있다.

카테고리를 그룹화할 때 카테고리에서 예상 대상 값을 추정하는 Target Statics (TS)를 사용한다. TS를 새로운 수치 특성으로 간주하는 것이 유용하다. 이러한 TS 특성은 계산 및 저장이 각 카테고리 당 하나의 숫자만 필요하므로, 최소한의 정보 손실로 범주형 특성을 처리하는 가장 효율적인 방법이다. 이 논문에서는 TS를 계산하는 방법에 중점을 두고 있다.

Target statistics

k번째 훈련 예시의 범주 xi k를 목표 통계량(TS) xi k와 같은 하나의 수치 특성으로 대체하는 것이 범주형 특성 i를 다루는 효율적인 방법이다.

• Greedy TS 타깃 변수 y의 조건부 기대값 E( y | xi = xik)을 동일한 범주 xik를 가진 훈련 데이터의 y 값의 평균으로 추정하는 탐욕적 목표 통계량 방법이다. 저빈도 범주에서 노이즈가 많은 추정치를 생성할 수 있어, 사전 확률 p에 의해 추정치를 다듬는다. 문제점은 목표 누설(target leakage)로, 특성 xk가 해당 훈련 데이터의 타깃 yk를 사용하여 계산되기 때문에 훈련과 테스트 예제의 xi y 분포가 달라질 수 있다는 것이다. 이를 해결하기 위해 목표 통계량의 성질 P1은 아래와 같아야 한다.
  
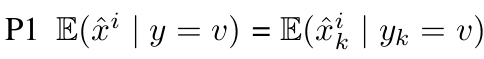
• Holdout TS 훈련 데이터 셋을 D0과 D1으로 나누고, D0을 사용하여 TS를 계산하고 D1에서 모델 훈련을 진행하는 방법이다. 성질 P1은 만족하지만 TS 계산과 모델 훈련에 사용되는 데이터의 양을 크게 줄이므로 모든 훈련데이터를 효과적으로 사용해야 한다는 P2를 지키지 못함
  
• Leave-one-out TS 훈련 예제 xk의 경우 Dk = D\xk를 사용하고 테스트 예제의 경우 Dk = D를 사용한다. 이는 타겟 누출을 방지하지 못한다.
  
• Ordered TS CatBoost는 정렬된 목표 통계량(Ordered TS)을 사용한다. 이 방법은 훈련 예제를 시간 순으로 처리하는 온라인 학습에서 영감을 받아, 훈련 데이터의 임의 순열을 이용하여 각 예제의 TS를 이전 데이터만을 사용하여 계산한다. 이는 타겟 누설을 방지하고 모든 훈련 데이터를 활용하여 모델을 학습하는 두 가지 주요 요구 사항(P1과 P2)을 만족시킨다. 또한, 분산 문제를 완화하기 위해 CatBoost는 그라디언트 부스팅의 다른 단계마다 다른 데이터 순열을 사용한다.
  

Prediction shift and ordered boosting

Prediction Shift

그라디언트 부스팅에서 발생하는 예측 이동 문제에 대해 설명한다. 예측 이동은 타겟 누설에 의해 발생한다. 이를 해결하기 위해 정렬된 목표 통계량(Ordered TS) 방법과 유사한 '정렬된 부스팅'이라는 방법을 제안한다.

기존 그라디언트 부스팅 절차에서는 예상치를 알 수 없으므로, 보통 같은 데이터셋 D를 사용하여 근사한다. 이 과정에서 몇 가지 이동이 발생하는데, 1) 훈련 데이터의 조건부 분포가 테스트 예제의 분포와 달라지고, 2) 이로 인해 기본 예측기가 편향되며, 3) 최종적으로 훈련된 모델의 일반화 능력에 영향을 준다. 이 모든 문제는 같은 데이터 포인트의 목표 값을 사용하여 각 단계의 기울기를 추정함으로써 발생하는 타겟 누설 때문이다. 이 현상을 '예측 이동'이라고 한다.

• Related work on prediction shift

  그라디언트의 조건부 분포 변화는 언급되었으나, 이 변화의 존재 여부는 공식적으로 정의되거나 이론적으로 증명되지 않았다. out-of-bag 추정을 바탕으로 iterated bagging을 제안했으나, 이 방법으로 계산된 잔차 추정치에는 여전히 변화가 있다. 또한, 배깅 방식은 데이터 처리 시간을 증가시킨다. 각 반복에서의 데이터셋 서브샘플링은 이 문제를 추론적으로 다루며 문제를 완화하기만 한다.
  

• Analysis of prediction shift

  예측 이동 문제를 간단한 회귀 작업과 이차 손실 함수를 사용하여 분석한다.

  두 독립적인 베르누이 변수 x1, x2 를 특성으로 하며, 두 단계의 그라디언트 부스팅을 거쳐 모델 𝐹=𝐹2=ℎ1+ℎ2를 생성다. 첫 번째 트리 ℎ1은 𝑥1에, 두 번째 트리 ℎ2는 𝑥2에 기반한다. 이는 특성 간의 비대칭성을 반영하는 설정이다.
  

• Theorem 1

  정리 1에 따르면, 독립적인 샘플 𝐷1과 𝐷2를 사용하여 각각 ℎ1과 ℎ2를 추정할 때, 훈련된 모델 𝐹2(𝑥)는 실제 함수 𝑓(𝑥)의 편향되지 않은 추정치가 된다.

  그러나 같은 데이터셋 𝐷를 사용하여 ℎ1과 ℎ2를 추정하면,

  𝐹2(𝑥)의 기대값은 𝑓(𝑥)에서 아래와 같이 편향되며 오차는 O(1/2^n)가 되어 데이터 크기 n에 반비례하는 편향이 발생한다. 이 편향은 c2에 비례한다.

  

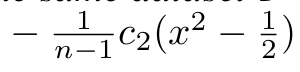
  이 정리는 두 가지 중요한 사실을 보여준다 :

  • 독립적 데이터셋을 사용할 때는 모델이 실제 의존성을 정확하게 추정

  • 같은 데이터셋을 사용할 경우 예측 이동이 발생하여 모델의 일반화 능력에 부정적인 영향을 미친다

    이러한 예측 이동은 타깃 누설, 즉 𝑦𝑘를 사용하여 𝑥𝑖𝑘를 계산하는 과정에서 발생하는 조건부 이동 문제와 유사하다.

Ordered Boosting

'정렬된 부스팅' 알고리즘은 예측 이동 문제를 해결하기 위해 각 훈련 단계에서 독립적으로 샘플링된 새 데이터셋을 사용하여 잔차를 구한다. 실제로 레이블이 있는 데이터가 제한되어 있기 때문에, 이론적으로 각 훈련 예제에 대해 편향되지 않은 잔차를 유지하기 위해 다양한 모델을 동시에 유지하고, 특정 예제를 제외하고 학습된 모델을 사용하여 잔차를 계산한다.

그러나 이 방법은 n배의 복잡성과 메모리 요구 사항 증가로 인해 실용적으로 적용하기 어렵다. 이 문제를 해결하기 위해 CatBoost에서는 수정된 버전을 구현하여 실제 문제에 적용할 수 있도록 했다.

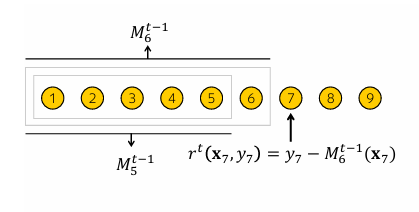
• Ordered boosting with categorical features 목표 통계량(TS) 계산과 정렬된 부스팅을 위해 훈련 예제의 임의 순열을 사용했다. 이 두 방법을 하나의 알고리즘으로 결합할 때, 예측 이동을 방지하기 위해 cat(카테고리 순열)과 boost(부스팅 순열)를 같게 설정해야 한다. 이는 훈련 과정에서 목표 변수 𝑦𝑖 가 사용되지 않도록 보장한다.
  

Practical implementation of ordered boosting

CatBoost는 'Ordered'와 'Plain' 두 가지 부스팅 모드를 제공한다. 'Plain' 모드는 표준 GBDT 알고리즘에 정렬된 목표 통계량(TS)을 포함하고, 'Ordered' 모드는 알고리즘 1의 수정 버전이다.

CatBoost는 훈련 시작 시 훈련 데이터셋에 대해 𝑠+1개의 독립적인 임의 순열을 생성한다. 이 중 순열 1부터 𝑠까지는 트리 구조를 정의하는 데 사용되고, 순열 0은 트리의 리프 값을 선택하는 데 사용된다.

특정 순열에서 짧은 역사를 가진 예제들은 높은 분산을 가질 수 있으므로, 여러 순열을 사용하여 이러한 분산을 감소시킬 수 있다.

• Building a Tree

CatBoost에서 기본 예측기로 사용되는 oblivious decision trees는 트리의 모든 레벨에서 같은 분할 기준을 적용하며, 이로 인해 트리는 균형 잡혀 있고 과적합에 덜 취약하다. 'Ordered boosting' 모드에서는 학습 과정 동안 순열에 따라 서로 다른 서포팅 모델 𝑀𝑟,𝑗를 유지하며, 이 모델들을 사용하여 범주형 특성에 대한 TS를 계산하고 그라디언트를 근사화한다.

이후 구성된 트리는 모든 서포팅 모델에 적용되어 각 모델을 부스팅한다. 'Plain boosting' 모드는 표준 GBDT 와 유사하게 동작하지만, 범주형 특성이 포함된 경우 해당 특성에 기반한 여러 서포팅 모델을 유지한다. 테스트 시 실행 속도를 높인다.

• Choosing leaf values 모든 트리가 구성된 후, 최종 모델𝐹의 리프 값은 두 모드에서 모두 표준 그라디언트 부스팅 절차를 통해 계산된다. 훈련 예제 𝑖는 𝑙𝑒𝑎𝑓0(𝑖) 에 매치되며, 여기서 순열 0을 사용하여 목표 통계량을 계산한다.
  
• Complexity CatBoost의 'Ordered' 모드에서는 계산 복잡도를 줄이는 기법을 사용한다. 특정한 최적화를 통해 𝑂(𝑠𝑛^2)개의 값을 가지는 대신, 로그 스케일로 감소된 수의 값만을 업데이트하고 저장하여, 지원 예측의 수를 𝑂(𝑠𝑛) 으로 줄인다. 이 방법은 계산 복잡도를 크게 감소시키며, CatBoost의 계산 효율을 향상시킨다.
  
• Feature combinations CatBoost에서는 범주형 특성의 조합을 추가적인 범주형 특성으로 사용한다. 데이터셋 내 범주형 특성 수에 따라 가능한 조합의 수가 너무 많아 모든 조합을 처리하는 것은 실현 불가능하기 때문에 CatBoost는 그리디 방식으로 조합을 구성한다. 트리를 분할할 때, CatBoost는 현재 트리에서 이전 분할에 이미 사용된 모든 범주형 특성을 데이터셋의 모든 범주형 특성과 결합한다. 이러한 조합은 실시간으로 목표 통계량으로 변환된다.
  
• Other important details CatBoost 알고리즘에는 두 가지 추가적인 옵션이 있다. 첫 번째는 부스팅 절차의 각 반복에서 데이터셋을 서브샘플링하는 것입이. 이 방법은 예측 이동 문제를 완전히 해결하지 못하지만, 효율적이어서 CatBoost의 두 모드에서 Bayesian bootstrap 절차로 구현되었다. 각 예제에는 가중치가 할당되며, 이는 그라디언트 계산 시 사용된다. 두 번째는 순열에서 첫 몇 개의 예제를 다루는 것으로, 이 예제들의 분산이 높을 경우 초기에 제외하여 계산의 정확성을 높인다.
  

Experiments

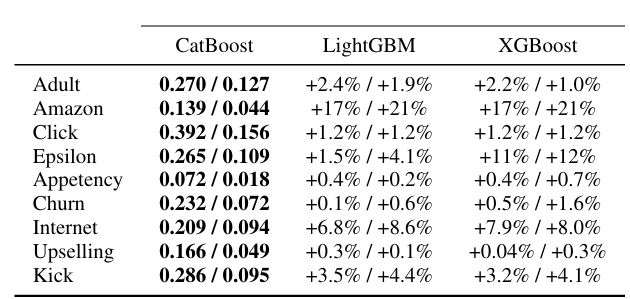
• Comparison with baselines CatBoost는 XGBoost와 LightGBM과 같은 오픈 소스 라이브러리와 여러 머신러닝 작업에서 비교되었다. 모든 학습 알고리즘은 정렬된 목표 통계량 방법을 사용하여 범주형 특성을 전처리했다. CatBoost의 'Ordered boosting' 모드는 다른 알고리즘보다 모든 데이터셋에서 우수한 성능을 보였으며, 통계적으로 유의미한 개선을 보였다.
  
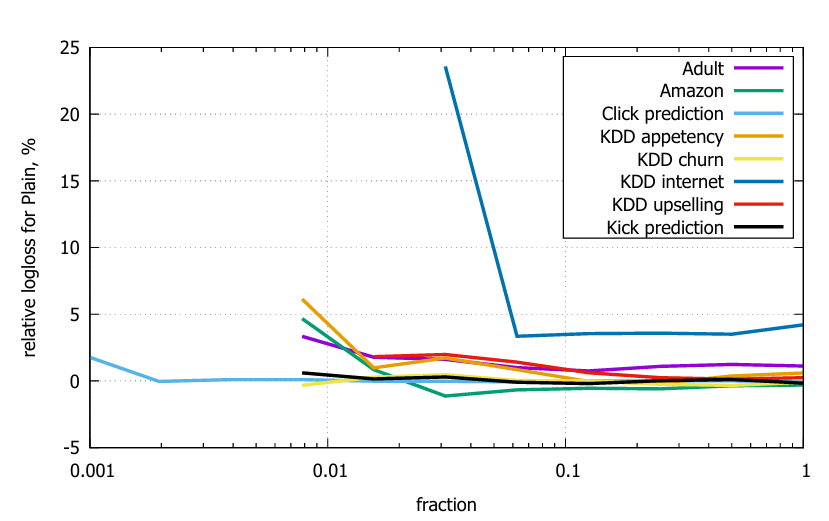
• Ordered and Plain modes Ordered 모드는 특히 작은 데이터셋에서 유용하며, Adult 및 Internet 데이터셋과 같이 작은 규모의 데이터셋에서 큰 이점이 있다. 작은 데이터셋에서는 편향이 성능에 부정적인 영향을 미친다. 또한, Plain 모드와 Ordered 모드를 무작위로 필터링된 데이터셋에서 비교한 결과, 작은 데이터셋에서는 Plain 모드의 상대적 성능이 떨어진다.
  
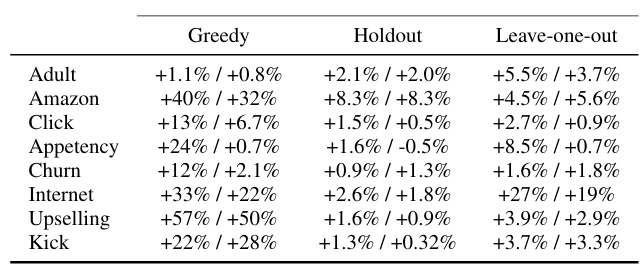
• Analysis of target statistics Ordered TS를 사용한 CatBoost는 다른 모든 접근 방식을 크게 능가했습니다. Holdout TS는 조건부 이동 문제(P1)에서 자유롭지만 훈련 데이터 사용이 덜 효율적(P2)이기 때문에 CatBoost보다 성능이 떨어진다. Greedy TS는 저빈도 범주에서 문제가 발생하고, Leave-one-out TS는 고빈도 범주에서도 문제가 발생한다.
  
• Feature combinations 특성 조합 수(cmax)를 1에서 2로 변경할 때 평균 logloss가 1.86% 개선되었고, 1에서 3으로 변경하면 2.04% 개선되는 등 뚜렷한 개선 효과를 보였다. cmax를 더 늘려도 성능에는 큰 영향을 미치지 않았다.
  
• Number of permutations 순열의 수(s)를 증가시킬 때 logloss가 약간 감소하는 경향을 보였다. 예를 들어, s=3에서는 0.19%, s=9에서는 0.38% 감소했다.
  

Conclusion

이 논문에서 우리는 그래디언트 부스팅의 모든 기존 구현에 존재하는 예측 이동의 문제를 식별하고 분석한다. ordered boosting with ordered TS을 통해 해결할 것을 제안한다. 이는 새로운 그래디언트 부스팅 라이브러리인 CatBoost에서 구현된다. 실증적 결과에 따르면 CatBoost는 주요 GBDT 패키지를 능가하며 공통 벤치마크에서 새로운 최첨단 결과를 얻을 수 있다.