https://arxiv.org/pdf/2211.15736
Abstract
이 논문에서는 전통적인 노이즈 감소 시뮬레이션 모델의 느린 생성 과정을 가속화하는 새로운 접근 방식을 제안한다. 현재 모델들은 매 반복마다 무거운 네트워크를 이용해 노이즈를 추정하며, 이 과정이 시간이 많이 걸리기 때문에 특히 엣지 기기에서의 활용이 제한된다. 이 연구에서는 노이즈 추정 네트워크를 압축하는 것에 초점을 맞추어 DM의 생성 속도를 향상시킨다.
주로 사용되는 압축 방식 대신, (Post Training Quantization) PTQ를 도입하여 DM의 다중 시간 단계 구조에 맞춘 양자화 방법을 개발한다. 이 방법은 교육 없이도 DM을 8비트 모델로 효과적으로 변환할 수 있으며, 성능을 유지하거나 향상시킬 수 있다. 또한, 이 기법은 다른 빠른 샘플링 방법과 함께 사용될 수 있는 plug-and-play 모듈로도 가능하다.
Introduction
이 논문에서는 노이즈 감소 확산 모델(denoising diffusion models)의 생성 과정을 가속화하는 새로운 방법을 제안한다. 생성적 적대 신경망(GANs)에 비해 우수한 품질과 다양성을 제공한다.
확산 모델은 실제 데이터를 가우시안 노이즈로 점진적으로 변환한 다음, 이 과정을 반대로 수행하여 실제 데이터를 생성하는 denoising 과정을 포함한다. 이 과정은 수천 번의 시간 단계에 걸쳐 무거운 신경망을 통해 노이즈 추정을 반복해야 하므로, 긴 반복 과정과 높은 추론 비용이 필요하다.
이 과정을 가속화하기 위한 이전의 방법들은 노이즈 추정을 위한 무거운 네트워크를 고려하지 않았다. 여기서는 학습 데이터의 접근성 및 비용 문제로 인해 기존의 훈련 의존적 네트워크 압축 방법이 적합하지 않기 때문에, 훈련 없는 네트워크 압축 기술인 Post Training Quantization(PTQ)를 도입했다.
PTQ는 계산 속도를 향상시키고 확산 모델의 무게를 줄이는 데 도움이 되지만, DM의 구조적 특성 때문에 구현이 힘들다. 특히, 시간 단계에 따라 변하는 노이즈 추정 네트워크의 출력 분포는 기존의 PTQ 방법들이 실패하는 이유이다.
이에 따라, 시간 단계 별로 변하는 분포를 고려한 새로운 PTQ 방법을 개발했다. 이는 'Normally Distributed Time-step Calibration (NDTC)'로, 비대칭 정규 분포에서 시간 단계를 샘플링하고, 이 시간 단계에 따라 교정 샘플을 생성한다. 이는 PTQ의 성능을 향상시킨다.
이 연구는 훈련 없이 확산 모델을 8비트로 양자화할 수 있는 PTQ4DM 방법을 제안하며, 이는 다른 최신 확산 모델 가속 방법에 플러그 앤 플레이 모듈로서 사용가능하다. 이는 확산 모델 가속화의 새로운 관점을 제시하며, 학습에 의존하지 않는 네트워크 압축을 통해 이루어진다.
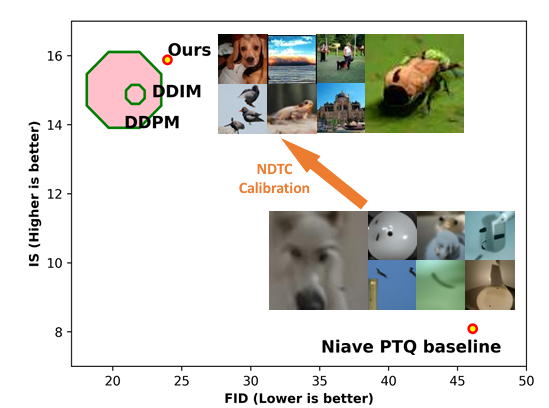
NDTC Calibration을 통한 추론 시간의 감소
Related Work
Diffusion Model Acceleration
확산 확률 모델(DMs)의 긴 반복 과정과 높은 비용 문제를 해결하기 위해 샘플링 궤적을 단축하는 방법들을 다룬다. 연구들은 더 짧은 시간 단계에서 효과적인 궤적을 찾는 데 초점을 맞추고 있으며, 다양한 방법으로 샘플링 효율을 개선하려고 시도합니다. 격자 탐색, 동적 프로그래밍, 비마르코프 확산 과정, 미분 방정식 활용 등을 사용했다.
그러나 이 논문은 단순히 샘플링 궤적을 단축하는 것 이상으로, 각 노이즈 추정 반복에서 네트워크를 압축함으로써 확산 모델을 더욱 가속화할 수 있다는 새로운 접근 방식을 제시한다. 특히, 사전에 훈련된 모델을 양자화하여 계산 속도를 높이고 자원 사용을 줄이는 방법인 PTQ를 활용하여 DM의 가속화를 구현한다.
이 연구는 PTQ4DM 방법을 통해 처음으로 확산 모델을 사후 훈련 방식으로 양자화하며, 이는 기존의 빠른 샘플링 방법들과 병행하여 사용할 수 있는 플러그 앤 플레이 모듈을 가능하게 한다. DM 가속화에 있어서 획기적인 발전을 나타낸다.
Post-training Quantization
신경망을 압축하는 효과적인 방법 중 하나는 양자화이다. 양자화 방법에는 크게 두 가지가 있다.
- Quantization-aware training, QAT: 네트워크 훈련 단계에서 양자화를 고려한다
- Post-training quantization, PTQ: 훈련 후 네트워크를 양자화한다. 이는 비교적 적은 시간과 계산 자원을 소모하기 때문에 네트워크 배포에 널리 사용된다.
PTQ의 주된 작업은 각 계층의 가중치와 활성화에 대한 양자화 매개변수를 설정하는 것으로, 이 과정에서는 clamp 함수를 사용하여 양자화된 값을 특정 범위([pmin, pmax]) 내로 제한한다.
양자화 매개변수를 설정할 때는 일반적으로 양자화 전후의 텐서의 평균 제곱 오차(MSE)를 최소화하는 매개변수를 선택한다. PTQ를 위한 활성화 계산 시 사용되는 교정 샘플의 수는 선택된 양자화 매개변수에 영향을 준다. 연구에 따르면 교정 샘플의 수가 양자화 결과에 중요한 영향을 미친다.
Zero-shot 양자화(ZSQ)는 PTQ의 특별한 경우로, 네트워크에 기록된 정보를 바탕으로 교정 데이터셋을 생성한다. 이 방법은 경사 하강법을 사용하여 네트워크 활성화의 분포가 실제 샘플의 분포와 유사하게 만든다. 확산 모델의 노이즈에서 이미지를 생성하는 과정은 네트워크 추론만을 사용하며, 이는 기존의 ZSQ 방법과는 다르다.
PTQ on Diffusion Models
Preliminaries
-
Diffusion Models
확산 확률 모델(Diffusion Probabilistic Model, DPM)은 Variational Lower Bound, LVLB를 최적화하여 훈련된다. 이 모델은 소량의 isotropic Gaussian noise를 점진적으로 추가하여 일련의 잠재 상태를 생성하며 이 과정은 마르코프 체인을 따른. T가 충분히 큰 경우, xt는 isotropic Gaussian 분포와 동일하게 된다 .
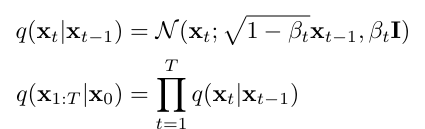
확산 모델은 입력 x0에 직접 조건을 부여함으로써 임의의 시간 단계 t에서 xt를 샘플링할 수 있다. 그러나 데이터 분포 q(x0)에 따라 달라지는 q(xt-1|xt)는 추적할 수 없으므로, 신경망을 매개변수화하여 이를 근사해야 한다. 이를 위해 변분 하한을 사용하여 음의 로그 우도를 최적화한다.
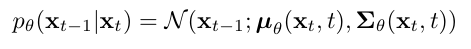
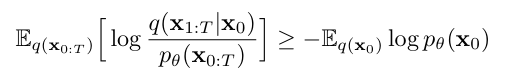
확산 모델의 노이즈 추정 과정은 매우 길고 복잡한 네트워크를 사용하며, 이로 인해 추론 과정이 비용이 많이 들기 때문에 확산 모델을 일반적인 PTQ 방법으로 단순하게 일반화하기 어렵다.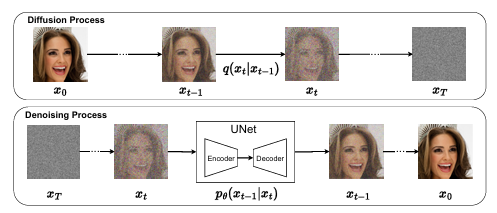
노이즈 제거를 반복하는 과정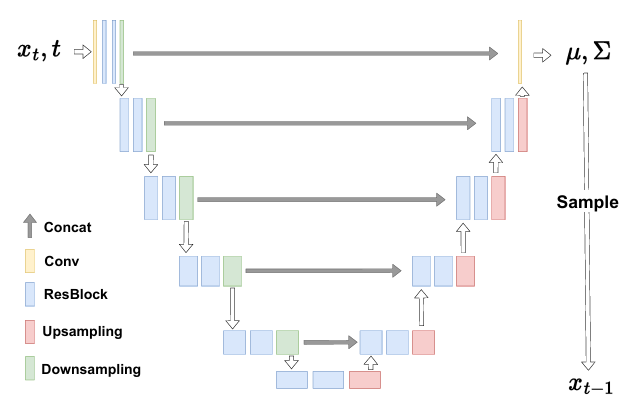
노이즈를 추정하기 위한 네트워크
-
Post-training Quantization
잘 훈련된 네트워크에서 각 계층의 가중치 텐서와 활성화 텐서를 위한 양자화 매개변수를 선택한다. 양자화 매개변수, 스케일링 인자(s), 제로 포인트(z)를 사용하여 텐서를 양자화된 텐서로 변환한다. 매개변수 선택의 가장 일반적인 방법은 양자화로 인한 오류를 최소화하는 것이다. 양자화 오류는 실제 텐서와의 거리를 평가하기 위한 메트릭 함수(MSE, 코사인 거리, L1 거리, KL 발산 등)를 사용하여 계산된다.
PTQ의 네트워크를 양자화하는 3단계 :
- 네트워크에서 양자화해야 하는 연산을 선택하고 다른 연산은 전체 정밀도로 둔다.
- 교정 샘플을 수집한다.교정 샘플의 분포는 실제 데이터의 분포와 최대한 유사해야 하며, 이는 양자화 매개변수가 교정 샘플에 과적합되는 것을 방지하기 위함이다.
- 가중치 텐서와 활성화 텐서를 위한 적절한 양자화 매개변수를 선택한다.
Exploration on Operation Selection
확산 모델에서 이미지 생성 과정을 분석하여 어떤 연산을 양자화할지 결정할지 분석한다. 확산 모델은 반복적으로 xt에서 xt-1로 이미지를 생성하며, 각 시간 단계에서의 입력은 xt와 시간 t, 출력은 평균 µ와 분산 Σ이다.
확산 모델의 네트워크는 주로 UNet과 유사한 CNN 구조를 사용하며, 양자화 대상은 계산 집약적인 컨볼루션 레이어와 완전 연결 레이어이다. 특별한 함수들은 정밀도를 유지하며, 네트워크의 출력(µ와 Σ)과 샘플링된 이미지(xt-1)도 양자화가 가능하다. 이는 해당 출력들이 양자화에 민감하지 않기 때문이다.
Exploration on Calibration Dataset
확산 모델을 양자화하기 위해 두번째 단계는 교정 샘플을 수집하는 것이다. 확산 모델에서는 훈련 데이터셋인 x0이 아닌 생성된 샘플 xt가 실제 네트워크 입력으로 사용된다. 이에 따라, 어떤 시간 단계에서 확산 과정이나 노이즈 감소 과정 중 생성된 샘플을 교정 샘플로 사용할지 결정해야 한다.
여러 직관적인 PTQ 기준을 전면적으로 조사한 결과, 특히 고안된 PTQ4DM 방법을 사용하여 8비트로 양자화된 확산 모델이 전체 정밀도 모델과 동일한 성능을 보여주었다. 8비트 모델은 32비트 모델의 성능과 비교할 때 경쟁력이 있음을 보여준다.
Analysis on PTQ Calibration and DMs
교정 샘플의 수집은 실제 데이터의 분포와 최대한 일치해야 하며, 이는 양자화 오류를 최소화하는 데 중요하다. 이전의 연구들은 단일 시간 단계의 시나리오에서 실제 훈련 데이터셋에서 직접 샘플을 수집하여 네트워크를 양자화했지만, 확산 모델을 위한 PTQ에서는 어렵다. 확산 모델의 경우 생성된 샘플 xt를 입력으로 사용하며, 이는 확산 과정이 정규 분포로 수렴하도록 매우 많은 시간 단계(T)를 포함한다. 이러한 다중 시간 단계 시나리오에서 효과적인 교정 데이터셋 수집 방법을 새롭게 설계해야 한다.
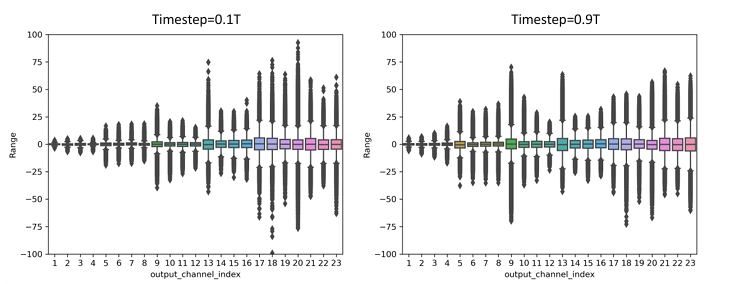
- Observation 0: Distributions of activations changes along with time-step changing. 확산 모델에서 활성화의 분포는 시간 단계에 따라 변화합니다. 이는 t1 = 0.1T와 t2 = 0.9T와 같은 다른 시간 단계에서의 활성화 분포를 분석함으로서 관찰됐다. 시간에 따라 분포가 변하기 때문에, 시간적으로 불변인 교정을 전제로 하는 다중 시간 단계 모델인 확산 모델에는 적용하기 어렵다. 이로 인해 다양한 시간 단계에서의 활성화 분포가 크게 다르게 나타나며, 이는 기존의 PTQ 교정 방법들이 확산 모델에 적합하지 않다.
- Observation 1: 노이즈 제거 과정에서 생성된 샘플은 교정에 더 유용하다. 확산 모델의 PTQ 교정을 위한 샘플 생성에는 두 가지 주요 방법이 있다: 1) 확산 과정에 원본 이미지를 사용 2) 노이즈 감소 과정에 노이즈를 사용 이전 방법들은 주로 훈련 세트의 분포를 대표하는 원본 이미지를 사용했다. 실험에서는 확산 과정용 원본 이미지와 노이즈 감소 과정용 가우시안 노이즈로 교정 세트를 별도로 수집하고, 이를 통해 양자화된 모델을 교정했다. 결과적으로, 확산 과정의 입력 노이즈가 양자화된 확산 모델을 교정하는 데 더 효과적인 것으로 나타났다. 입력 노이즈가 양자화된 모델의 교정에 더욱 유용하다.
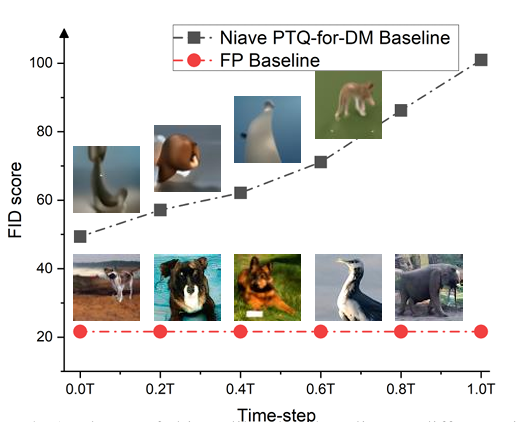
- Observation 2: 실제 이미지 x0에 가까운 샘플 xt는 보정에 더 유용하다. 확산 모델(DM)을 위한 PTQ 교정의 기본 방법은 특정 시간 단계 t에서의 샘플인 xt를 사용하여 양자화된 모델을 교정하는 것이다. 전체 정밀도 노이즈 추정 네트워크를 사용하여 교정 세트로 xt를 생성하고, 이를 양자화된 네트워크 교정에 활용한다. 실험 결과, 이 간단한 방식으로 교정된 8비트 모델은 양적 및 질적으로 만족스러운 이미지를 생성하지 못했습니다. 그러나 실험에서는 시간 단계 t가 실제 이미지 x0에 가까워질수록 PTQ 교정의 효과가 증가한다는 것을 발견했다. 이는 노이즈 감소 과정에서 시간이 감소함에 따라 네트워크 출력의 분포가 실제 이미지의 분포와 유사해지기 때문이다.
- Observation 3: 다양한 시간 단계로 보정 샘플을 생성해야 한다. 다중 시간 단계 시나리오를 위해 수집된 교정 데이터셋과 달리 일반적인 방법은 단일 시간 단계 시나리오를 대상으로 한다. 확산 모델의 교정 데이터셋은 시간 단계에 따른 샘플의 차이를 반영해야 하며, 이를 위해 시간 단계 전체에서 균일하게 분포된 시간(t)을 샘플링하여 생성하는 방법을 사용한다. 이렇게 생성된 샘플은 다양한 시간 단계를 포괄할 수 있다. 실험을 통해 이 방식이 교정 샘플이 시간 단계 차이를 효과적으로 반영해야 함을 확인했으며, 이는 교정 데이터셋의 효과성을 입증했다.
Normally Distributed Time-step Calibration
다중 시간 단계 시나리오에 맞춘 특정 교정 샘플 수집 방법, 'Normally Distributed Time-step Calibration (NDTC)'을 제안한다. 이는 (1) 전체 정밀도 노이즈 추정 네트워크를 사용해 노이즈로부터 생성된 샘플을 포함하고, (2) 실제 이미지 x0에 가까운 시간 단계에서, (3) 다양한 시간 단계를 포괄하는 교정 샘플을 생성한다.
시간 단계 ti는 치우친 정규 분포에서 추출되어, 노이즈 감소 과정의 시간 단계 범위에서 균등하게 샘플링된다. NDTC 방법의 효과성은 PTQ 기준선 및 전체 정밀도 확산 모델과의 비교를 통해 평가되었고 효과적으로 교정 세트가 수집되었다.
Time step 별 샘플링 과정
Exploration on Parameter Calibration
교정 샘플이 수집되면, 세 번째 단계는 확산 모델의 텐서를 위한 양자화 매개변수를 선택하는 것이다. 텐서를 교정하기 위한 적합한 메트릭을 탐구한다. 평균 제곱 오차(MSE)가 L1 거리, 코사인 거리, KL 발산보다 더 나은 성능을 보여준다. 따라서 확산 모델을 양자화하는 데 MSE를 사용한다.

More Experiments
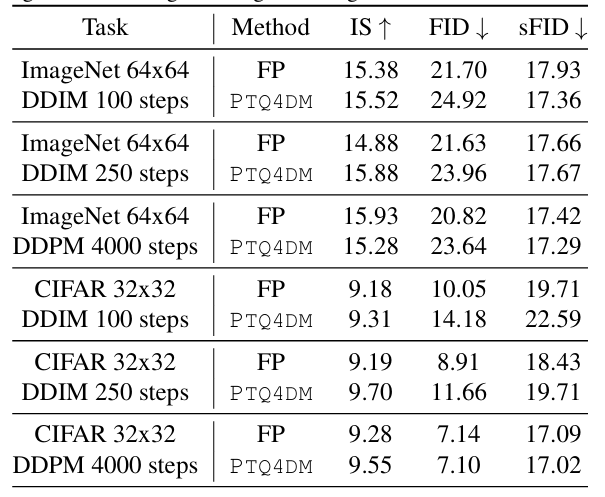
이 연구에서는 CIFAR-10과 다운샘플링된 64×64 ImageNet 이미지를 생성하기 위해 확산 모델을 선택했다. DDPM(4000단계)과 DDIM(100단계 및 250단계)을 사용하여 이미지를 생성하고, 1024개의 교정 샘플을 생성한 뒤 네트워크를 8비트로 양자화하여 10,000개의 이미지를 평가했다.
이 실험에서는 8비트로 양자화된 DDPM이 전체 정밀도의 DDPM보다 우수한 성능을 보였다. 이는 노이즈 추정 네트워크에도 중복성이 존재하며, 이는 긴 반복과 복잡한 네트워크 작업이 확산 모델의 노이즈 감소 과정을 늦추는 원인임을 보여준다. 이 결과는 확산 모델의 양자화와 관련하여 새로운 관점을 제공한다.
Conclusion
노이즈 감소 과정을 늦추는 두 가지 주요 요인
- 노이즈에서 이미지를 샘플링하기 위한 긴 반복
- 각 반복에서 노이즈를 추정하는 복잡한 네트워크
이러한 문제 중 두 번째 요인에 초점을 맞춰 Post-Training Quantization (PTQ) 방법을 확산 모델에 적용하여, 사전 훈련된 확산 모델을 성능 저하 없이 직접 8비트로 양자화할 수 있는 PTQ4DM을 제안한다. 이 방법은 DDIM과 같은 다른 빠른 샘플링 방법에 추가될 수 있다.
