[논문 리뷰] Deep Residual Learning for Image Recognition

주제

Skip Connection(Shortcut)을 통해 층이 깊어져도 학습이 가능하게 만들었고, Bottleneck 구조를 통해 연산 효율성을 챙겨서 훨씬 더 깊은 층(Layer)을 쌓을 수 있게 함

Abstract

층이 깊어져도 훈련을 쉽게 하기 위해서 “residual learning framework”를 제안함

• 입력에 대해 출력을 바로 학습하는 것이 아닌 입력에 대해 출력을 얼마나 더하면 될지를 학습하는 방식

이 방식은 최적화하기 쉽고 layer가 많아져도 정확도를 보장함

Introduction

층이 깊어질 수록 low/mid/high 레벨의 특징을 통합하기 때문에 특징들이 풍부해지지만, 층을 쌓는 것만큼 깊은 층을 학습하는 것은 쉽지 않다.

(원인1) “vanishing/exploding gradients” 문제

→ 정규화된 초기화와 중간 정규화 레이어를 통해 완화됨

• low/mid/high 레벨 특징: low→mid→high 로 갈 수록 더 넓은 정보 포함
  
• vanishing/exploding gradients 역전파를 통해 출력층의 Loss가 뒤에서부터 앞으로 가중치를 업데이트할 때 발생하는 문제
  • vanishing gradients: 1보다 작은 값을 계속 곱하게 되는 경우 0으로 수렴하여 앞쪽 층의 가중치들이 업데이트 되지 않는 경우
  • exploding gradients: 1보다 큰 값을 계속해서 곱하게 되는 경우 가중치가 너무 크게 변해서 수렴하지 않고 학습을 못함
• 정규화된 초기화 (Normalized Initialization) 가중치를 처음에 설정할 때 너무 크지도 않고 너무 작지도 않은 값으로 초기화
  
• 중간 정규화 레이어 (Intermediate Normalization Layers) 층을 지날 때마다 데이터를 평균 0, 분산 1인 데이터로 정규화하여 보냄 → Batch normalization이 이 방법의 한 종류
  

(원인2) Degradation 문제: 깊이가 깊어질 수록 trainig error 증가 (과적합이 아니라 optimization 문제)

→ 이를 해결하기 위해서 논문에서 Residual Learning 이라는 방법 제시

Residual learning

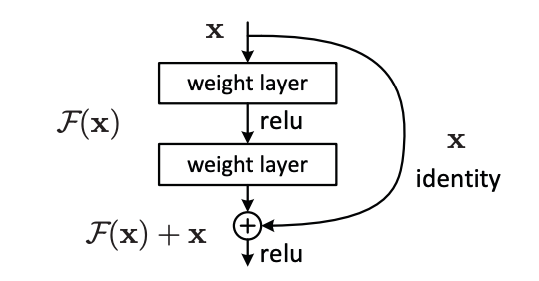
위에 블록에서 F(x)는 x → weight layer → ReLU → weight layer 인 비선형성 함수

H(x)를 학습하는 대신에 H(x) = x + F(x)로 표현해서 잔차인 F(x)만 학습하게 하는 방법

→ 항등 함수가 최적이라면 잔차인 F(x)를 0으로 만드는 것이 비선형 층들을 쌓아서 항등 함수로 근사하는 것보다 쉽다

→ F(x) + x는 shortcut connections (한 개이상의 층을 스킵)을 통해서 구현할 수 있다

F(x) = W2σ(W1x)

성능

이런 방법은 특정 데이터셋에만 국한되지 않고 ImageNet에 제출된 것 중에 가장 깊었고 VGG보다 더 낮은 복잡성을 가지고 있을 뿐만 아니라 일반화 성능도 좋다

Related Work

Residual Representations

• VLAD, Fisher Vector
• Multigrid: 편미분할 때 하위 문제들을 다양한 범위에서 reformulate하는 방법

Shortcut Connections

• MLP에서 선형 레이어 추가하거나 중간 레이어가 분류기에 바로 연결되는 방법
• Highway networks: gate 함수를 가진 shortcut connection 제안 → gated shortcut이 닫히면 non-residual
  

Deep Residual Learning

Residual Learning

H(x)를 근사하게 하는 것이 아니라 잔차 함수인 F(x) = H(x) - x를 근사하게 만듦

추가된 레이어들이 항등 함수라면 깊은 모델은 얕은 모델보다 training error가 크지 않아야 함 (최소한 입력만큼의 출력은 보장하니까?)

Degradation 문제는 깊은 네트워크가 여러 비선형 레이어를 통해 항등 함수를 학습하기 어렵다는 데서 발생한다.

Residual learning은 F(x) = 0이 되도록 함으로써 항등 함수를 효과적으로 근사할 수 있게 한다.

Identity Mapping by Shortcuts

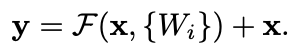
• 추가 매개변수가 필요없고 계산 복잡하지 않음 (shortcut에서 입력 x 더할 때 추가적인 가중치 행렬이나 추가적인 연산이 없음)
• 입력과 출력의 차원이 동일함

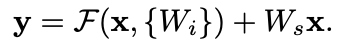
• 입력과 출력의 차원이 동일하지 않을 경우 W_s를 곱해서 차원을 맞출 수 있음

Network Architectures

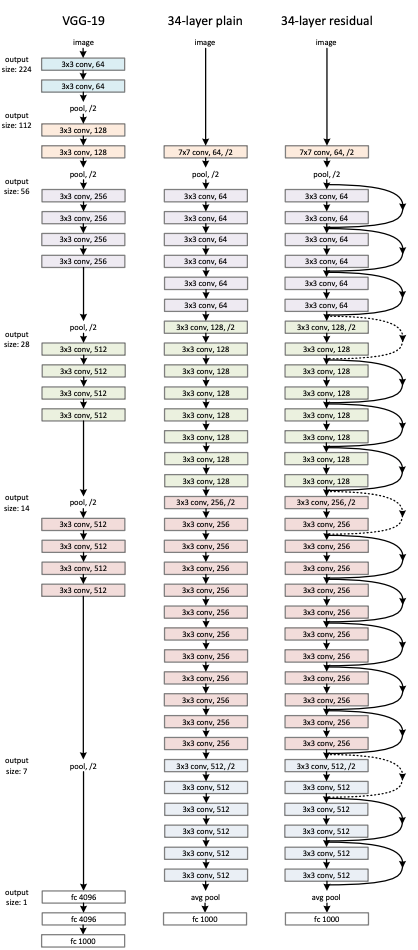
VGG Net (왼쪽) / baseline (중간)

• 대부분 3x3 필터 사용

1. 피쳐맵의 사이즈가 같음 → 필터의 수 (채널 수)도 똑같이 맞춤
2. 피쳐맵의 사이즈가 1/2 → 필터의 수 (채널 수)는 2배

→ VGG보다 baseline이 같은 크기의 피쳐맵을 처리할 때보다 더 필터 수가 적다

Residual Network (오른쪽)

• shortcut connection 추가
• 차원 증가하는 경우 → 점선 연산
  • 옆의 두 모델은 입력과 출력을 다시 더하지 않기 때문에 차원을 맞춰주는 게 필요 없음
  • residual connection에서는 x + F(x) 와 같은 연산을 하기 때문에 차원 맞춰줘야 함
  • 채널 차원 맞추는 방법 (H x W x C 중 C) 1) 늘어난 차원에 대해서 0으로 패딩

    • 28 x 28 x 64 → 28 x 28 x 128일 때 다른 부분을 0으로 채움

      2) W_s를 입력에 곱해서 맞춤

    • 28 x 28 x 64 → 28 x 28 x 128

    • W_s: 1×1 conv, out_channels=128

  • H x W 차원 맞추는 방법: stride 2 → shortcut (x)는 56 x 56이고 F(x)는 28 x 28이라서 shortcut에 stride 2해서 맞춤
    

Implementation

• 각 Conv → Batch normalization → optimization
  • BN을 통해서 forward propagation 할 때 0이 아닌 분산 갖고, backward propagation 할 때 healthy norm 갖게 함 → forward나 backward에서 vanish 일어나지 않음
• 가중치 초기화 진행
• 256 배치 사이즈 SGD, momentum = 0.9, 0.0001 weight decay
• learning rate는 0.1로 시작해서 오류 안정화될 때가지 1/10
• 60x10^4 iterations
• dropout 사용 안함

Experiments

ImageNet Classification

Plain networks

• plain network에서는 layer가 더 많은 게 ImageNet validation에서 Top-1 error (확률이 가장 높은 분류가 틀린 경우)가 높다
  
• 전체 과정에서 34 layer의 training error가 18 layer보다 높음 (얇은 선: training error, 굵은 선: validation error)
  
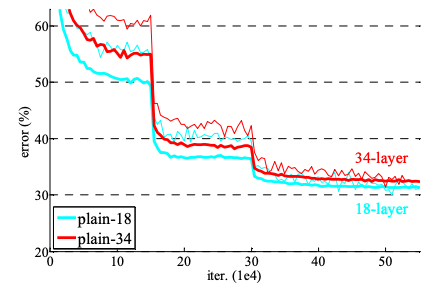
• plain-34도 충분히 좋은 정확도를 가지지만 깊어질 수록 수렴이 느려서 훈련 오류를 줄이는 데 문제가 발생함

Residual networks

• 34-layer가 더 오류가 낮으며 34-layer에서 plain과 비교했을 때 오류를 3.5% 낮춤
  
• 34-layer가 training error가 더 낮고, validation에서 더 일반화를 잘함
• 18-layer에서 초반에는 빠르게 수렴하기 때문에 최적화가 용이함

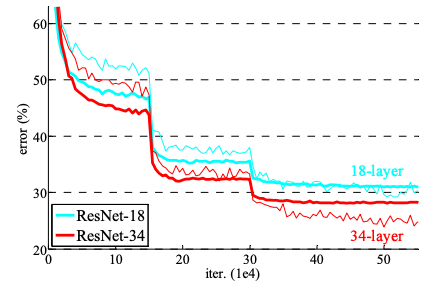
⇒ degradation 문제가 완화될 수 있고 깊이가 깊어져도 정확도를 얻을 수 있다는 것을 보여줌

Identity vs. Projection Shortcuts

(A) 차원 늘릴 때, zero padding shortcuts (parameter free)

(B) 차원 늘릴 때, projection shortcuts 사용하고 나머지는 identity shortcuts

(C) 항상 projection shortcuts

⇒ (C)는 연산량이 많지만 세 방법 사이에서 큰 성능 차이가 없어서 (C) 방법은 사용 안함

⇒ Identity shortcuts은 bottleneck 구조에서 시간 복잡성을 줄일 때 중요함

Deeper Bottleneck Architectures

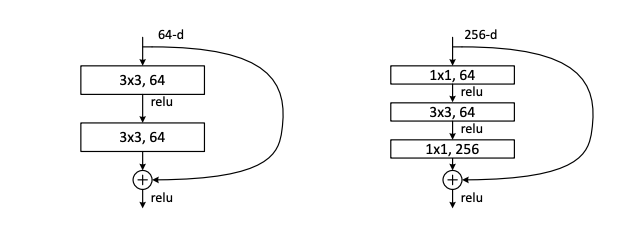
• 훈련 시간을 위해 bottleneck 디자인을 구상함 (오른쪽)
• Bottleneck Architecture
  • 입력: 256-d (차원)
  • 연산 1: 1x1 conv, 64-d (차원 축소)
  • 연산 2: 3x3 conv, 64-d
  • 연산 3: 1x1 conv, 256-d (차원 복구)
  • 출력: 256-d

⇒ parameter free인 identity shortcut을 통한 bottleneck 구조 → 두 개의 고차원 (256-d)를 연결했어도 효율적

50/101/152-layer ResNet

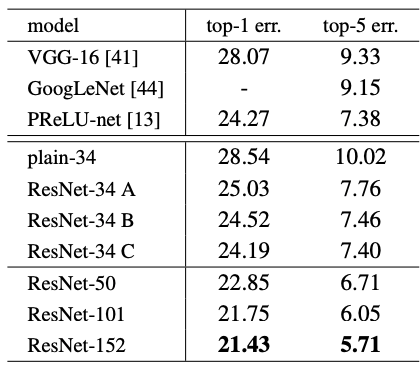
• 50/101/152 layer → 34 layer의 모델들보다 오류 낮음

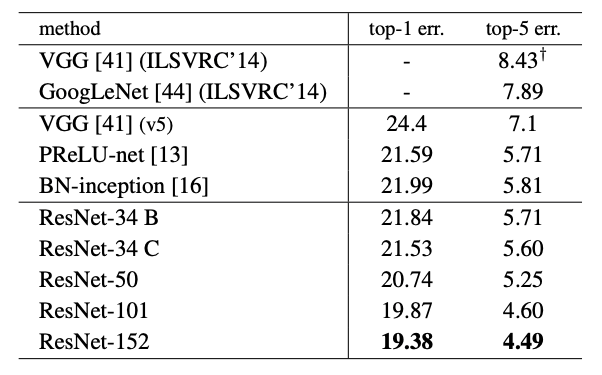
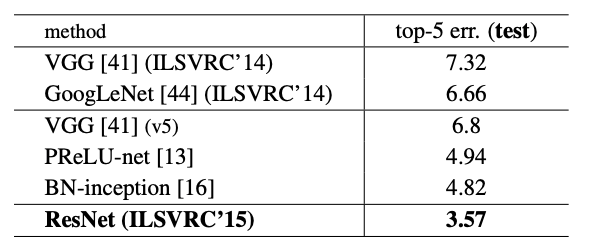
• 다른 앙상블 모델들보다도 ResNet 싱글 모델의 오류가 더 낮음
  

CIFAR-10 and Analysis

• Architecture

  단계	레이어 유형	출력 크기 (Feature Map)	필터 수 (Channels)	레이어 개수
  시작	3x3 Conv	32x32	16	1
  Stage 1	3x3 Conv 블록	32x32	16	2n
  Stage 2	3x3 Conv 블록	16x16	32	2n
  Stage 3	3x3 Conv 블록	8x8	64	2n
  종료	Global Avg Pool + FC	1x1	(10 classes)	1
  합계				6n + 2

• plain은 깊어지면 오류가 높아지지만 ResNet은 110 layer이 20 layer보다 오류 낮음
  
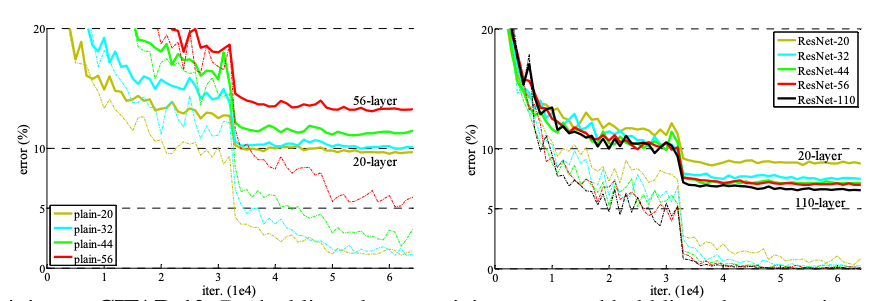
• 1202개 이상의 layer에서는 110 layer보다 성능이 안 좋은데, 이건 과적합때문 → maxout이나 dropout을 사용하면 해결할 수 있다 (이 논문에선 저 방법 사용 안함)

Object Detection on PASCAL and MS COCO

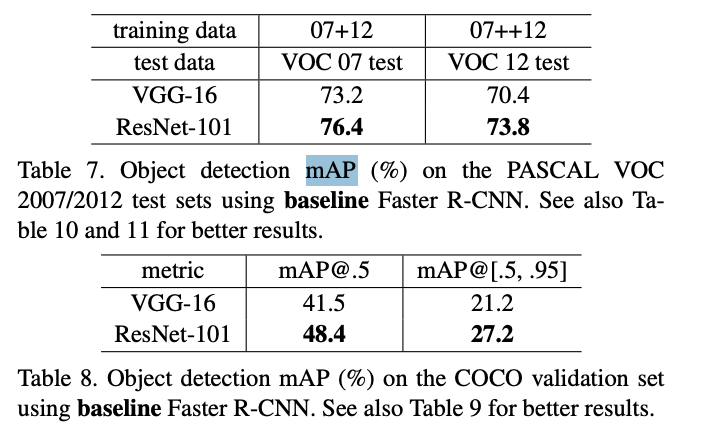
• 사물 인식에서도 좋은 일반화 성능을 가짐

용어 정리

• Fully Connected Layer: 각 출력 노드가 모든 입력과 연결됨
• Convolutional Layer: 입력의 patch마다 필터를 적용 → 특징 추출 (각 출력이 모든 입력과 연결되지 않고 일부 입력하고만 연결됨)
• 필터의 개수 (채널): 이 필터를 몇 종류나 사용할 것인지 (3x3 필터를 64개 사용 → 출력되는 피쳐맵 채널(깊이)는 64)