
Linear Regression (선형 회귀)
회귀 분석 종류 중 가장 대표적인 회귀 분석
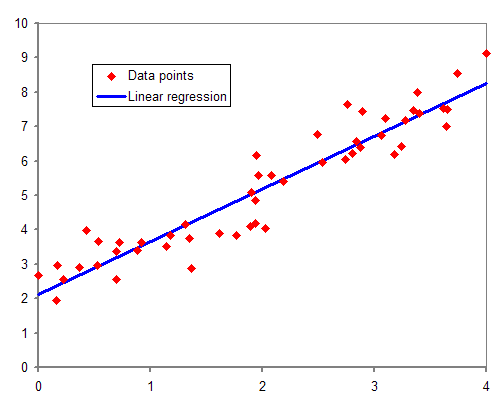
1. 선형회귀
선형 회귀 문제란?
- 독립 변수와 종속 변수간의 상관관계가 있어야 한다.
- 독립 변수와 종속 변수 데이터를 가지고 학습을 진행한 뒤, 새로운 독립 변수를 주었을 때 종속 변수의 값을 예측 하는 것.
예) 몸무게와 키 데이터를 가지고 학습한 뒤, 몸무게 만으로 키 예측하기.
공부시간과 시험 성적 데이터를 가지고 학습한 뒤, 공부 시간만으로 성적 예측하기 등.
(몸무게-키, 공부 시간-시험 성적 모두 상관관계를 가지고 있다.)
2. 원리 및 데이터
키를 가지고 몸무게를 예측하는 프로그램을 만든다고 가정을 하자.
- X 데이터 = 키
- Y 데이터 = 몸무게
X = [160, 172, 181, 183, 187, 193]
Y = [56, 64, 74, 86, 93, 104]
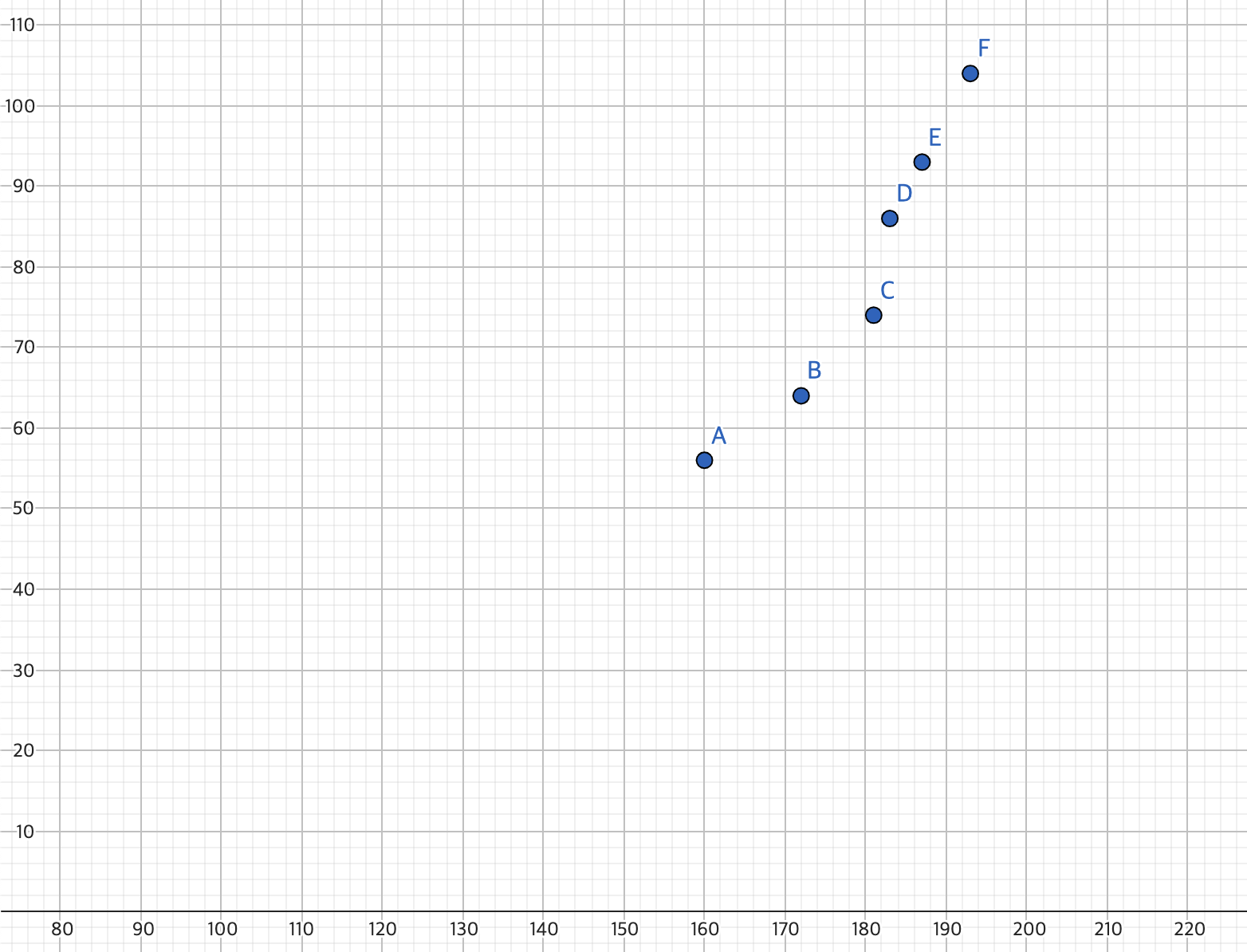
- 이 데이터를 가장 잘 일반화 할 수 있는 직선 하나를 찾는다. (직선 = 함수)
그 직선 함수를 H(x) 라고 하면, H(x) = aX + b 이다. (y = ax + b 꼴)
어떻게 하면 컴퓨터가 직선을 찾을 수 있을까?
3. 근사 (직선 구하는 법)
직선을 구하는 방법은 임의로 기울기와 절편을 초기화 한 뒤, 두 값을 바꿔가며 직선이 데이터를 잘 근사하는 시점의 값을 찾는다.
임의의 a (기울기), b (절편) 값 초기화
- a = 1, b = 1로 임의로 초기화 하겠다.
H(x) = 1X + 1
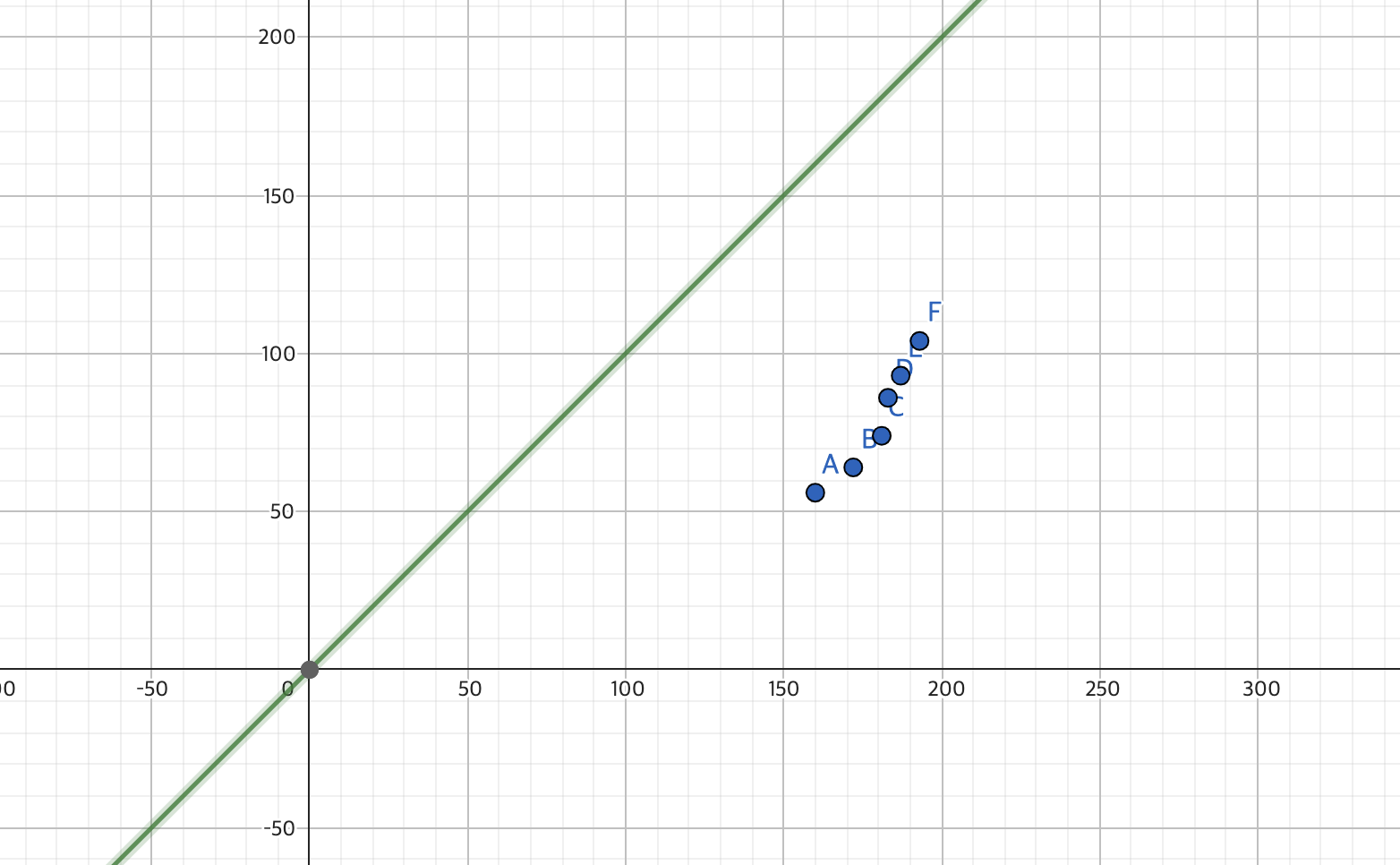
a (기울기), b (절편) 업데이트
이제 적절한 a와 b의 값을 찾아나가면 된다.
- 그러기 위해서는 얼마 만큼의 오차가 있고 어떤 방법으로 오차를 줄일지 정해야한다.
4. 오차 (Error)
Cost Fuction (Loss Fuction) (손실함수)
손실 함수는 우리가 예측한 값과 실제 데이터 값의 차이를 알기 위해서 쓰인다.
1. 오차를 구하는 방법
H(x)의 예측 값 (1X + 1)과 실제 데이터 Y의 차이는, 같은 X값에 대해서 각각의 Y값을 서로 빼주면 알 수 있다.
- Error = Y - (1X + 1)
데이터를 보면 키가 160(X)인 사람의 몸무게는 56(Y)이다
H(160) = 160(예측 값) 이다. (a=1, b=1 일 때)
즉 오차는 56 - 160 으로 -104 이다.
2. 오차가 음수가 나왔다.
즉 Y가 (1X + 1)보다 크면 양의 오차, 작으면 음의 오차가 나온다.
양의 오차든 음의 오차든, 오차는 오차이다. 하지만 양의 오차와 음의 오차를 더하면 오차가 없다는 결과가 나온다.
이 경우를 배제하기 위해서 절댓값을 취해, 모든 오차를 양의 오차로 만들어 준다.
- Error = | Y - (1X + 1) |
이러면 오차는 |56 - 160| 으로 104 이다.
+ 하지만 절댓 값을 취하면 구간을 나눠줘야해서 미분하기 어려워지고, 연산 속도가 떨어진다.
3. 절댓값 대신 제곱
절댓값 대신 제곱을 취해주고, (+ 제곱을 취해주면 오차가 커질수록 더 극대화 된다.)
모든 X에 대해서 오차를 구해야 하므로 시그마를 취해준다.
(Y는 실제 데이터 값이고, Y_hat은 H(x)의 예측 값이다.)

- 이것이 SSE Cost Function 이다.

- 단순 합산이 아닌 평균을 취해주면 MSE가 된다.
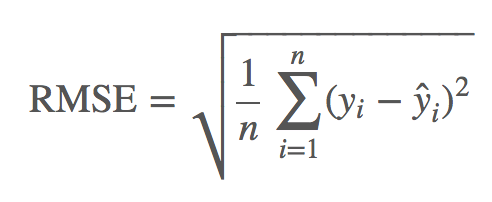
- MSE에 루트를 취해주면 RMSE가 된다.
<손실 함수 종류>
- SSE (sum squared error)
- MSE(Mean Square Error)
- RMSE(Root Mean Squared Error)
- Cross-entropy
등
이제 오차는 구했고, 어떻게 하면 그 오차를 줄여나갈 수 있을까?
5. 오차 줄이기 (Optimizer)
경사 하강법 (Gradient Descent)
Cost Function에서 실제 Y 데이터 값과 예측한 Y_hat 값의 차이를 구했다면, Optimizer는 그 구한 오차를 줄여나가는 법에 대해서 다룬다.
- 실제 Y 데이터 값은 고정되어있다.
- 오차는 |Y - H(x)|이기 때문에, 오차를 줄이기 위해서는 H(x) 함수의 aX + b 에서 a와 b의 값을 바꿔주어야한다.
(a, b를 파라미터라고 한다.)
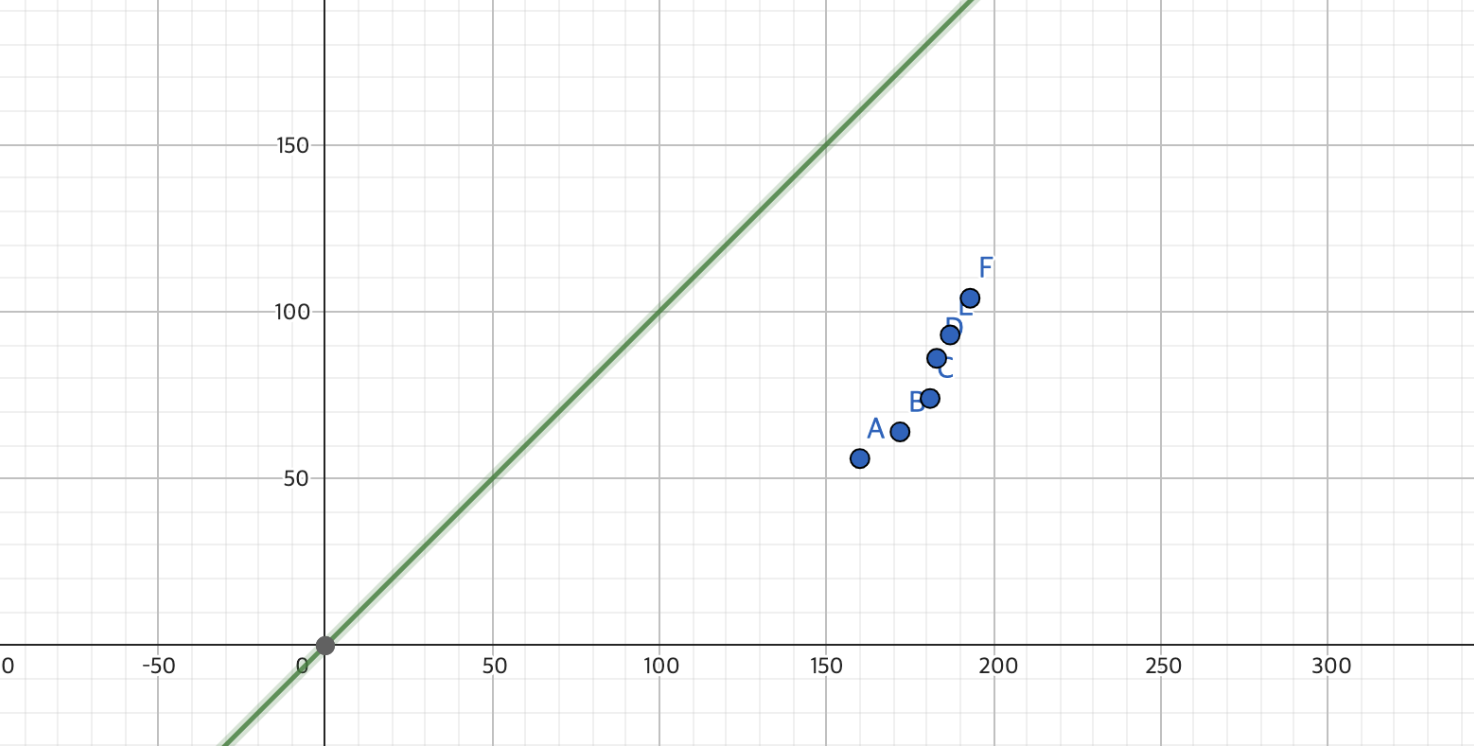
- 현재 파라미터를 임의로 초기화하여 a = 1, b=1 인 상태이다.
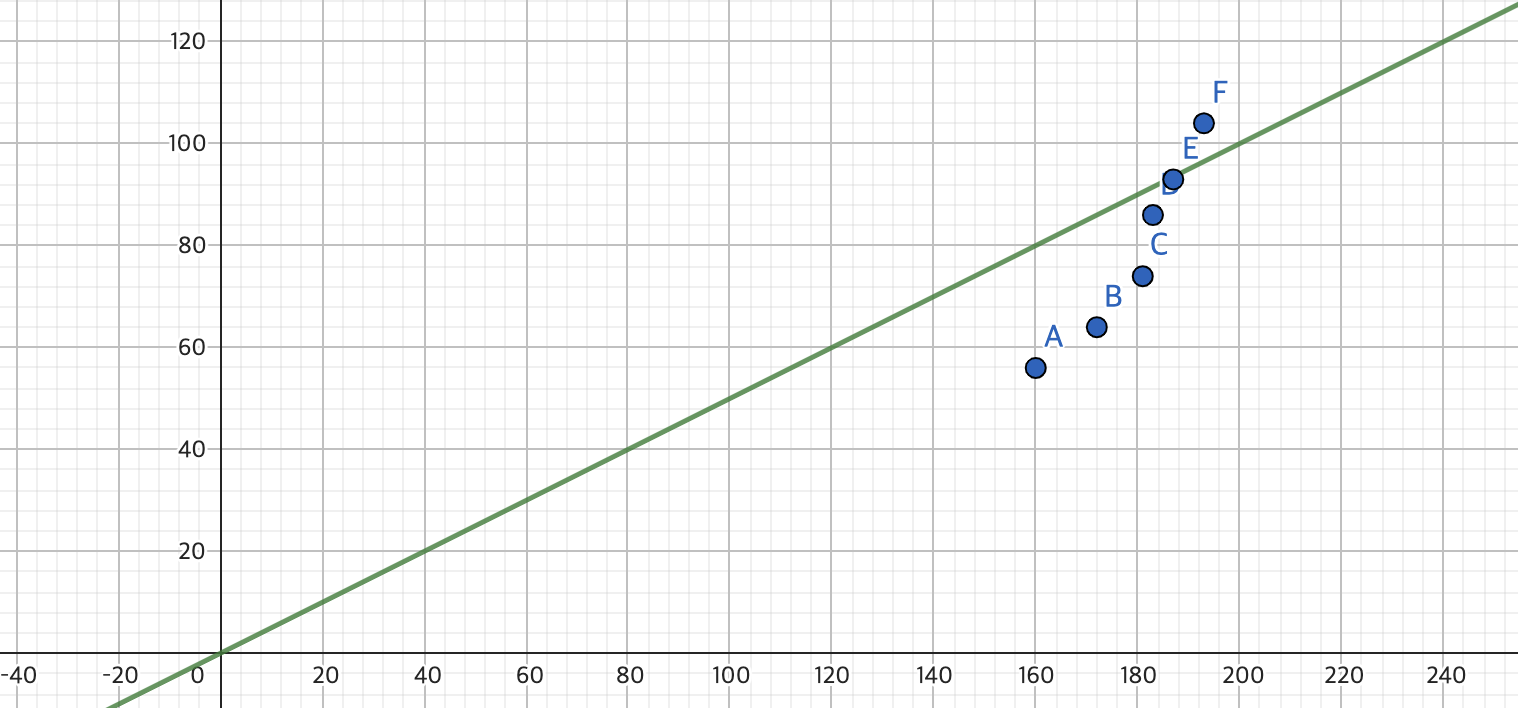
- a 값만 1에서 1/2로 바꾸어 보았다. (a = 1/2, b = 1)
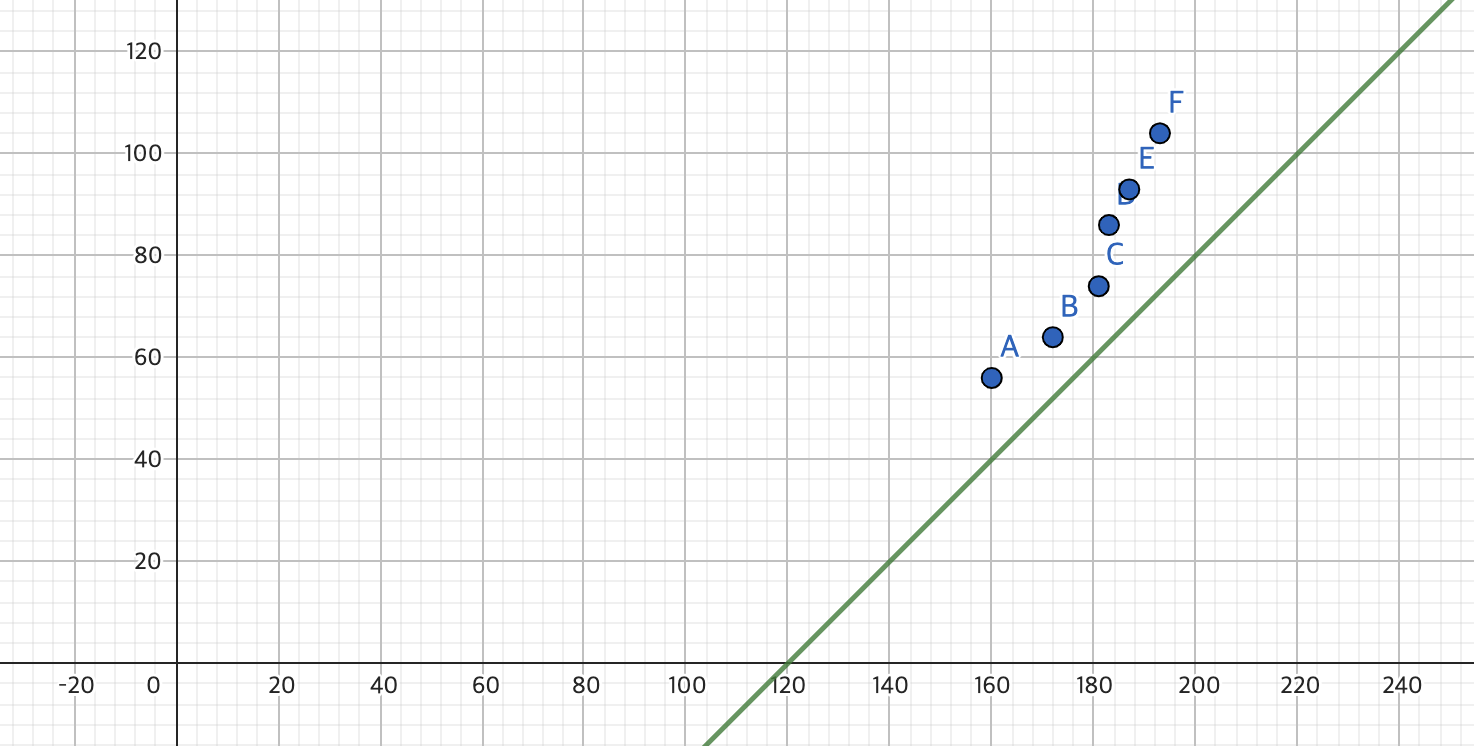
- 이번에는 a 값만 1로 두고 a만 -120으로 바꾸어 보았다. (a = 1, b = -120)
a, b값에 따라 Error 값이 확연히 바뀌는 것을 볼 수 있다.
즉 각각의 파라미터 θ(a, b)에 따른 Error 그래프를 그려보면
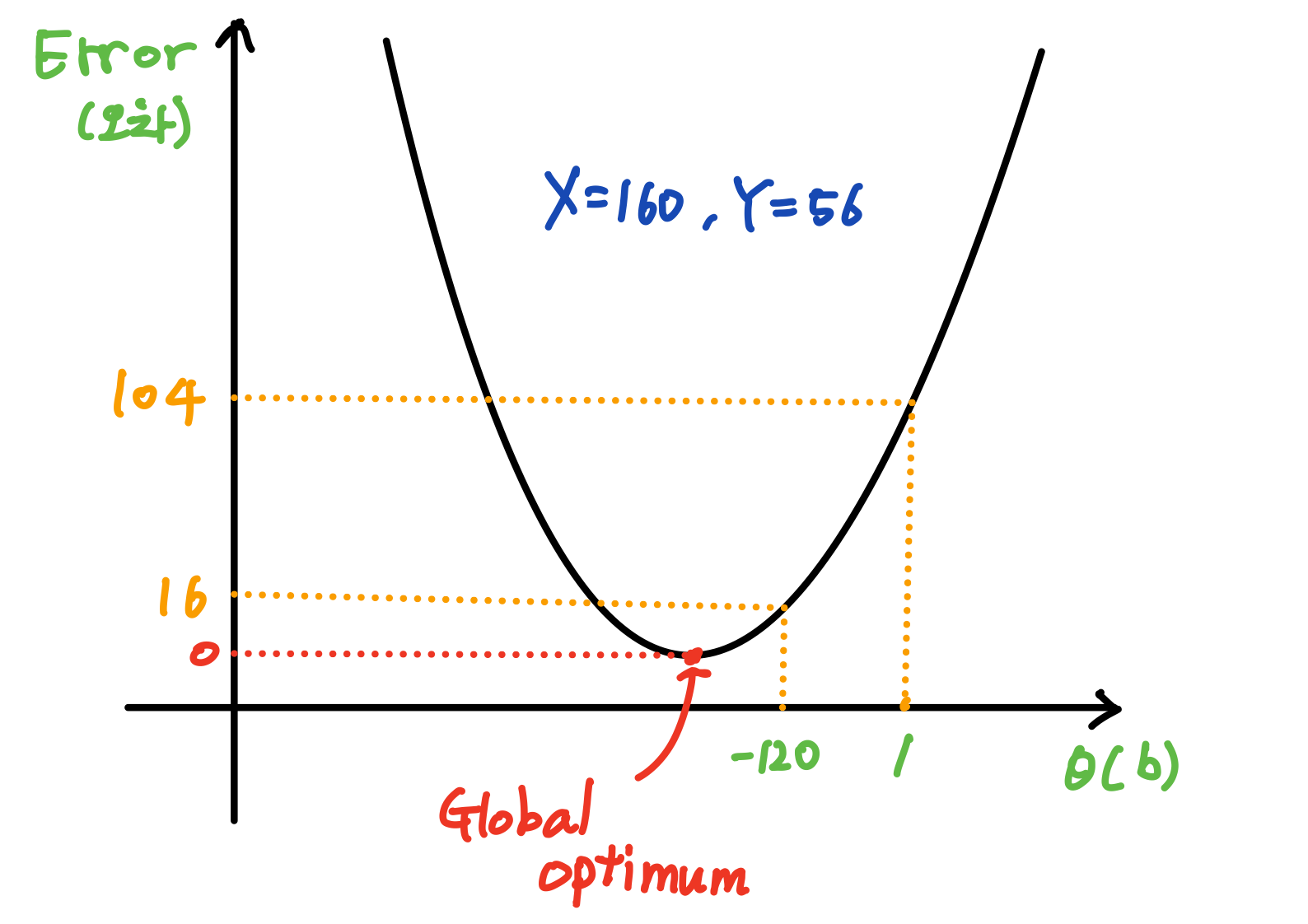
- b를 1에서 -120으로 바꾸면 Error가 16으로 줄어든다.
- 최적해를 가지는 Global Optimum (Error = 0)일 때의 θ(a, b) 값을 찾는 것이 목표이다.
- 최적해를 가질 때의 접선의 기울기 값은 0이다.
Cost Function의 접선의 기울기
기울기가 0이 되는 지점의 θ(a, b)를 구하면 된다.
- 기울기가 0이 되는 지점을 알기 전에, 기울기를 구하려면 미분을 해야한다.
- 현재 파라미터는 a와 b 두가지이다.
즉 기울기를 알기 위해서 a와 b에 대해서 각각 편미분을 진행해 기울기를 구하고, Error 값을 최소가 되도록 각각의 a와 b를 Update 하면 된다.
편미분 & 파라미터 θ (a, b)를 Update하는 방법
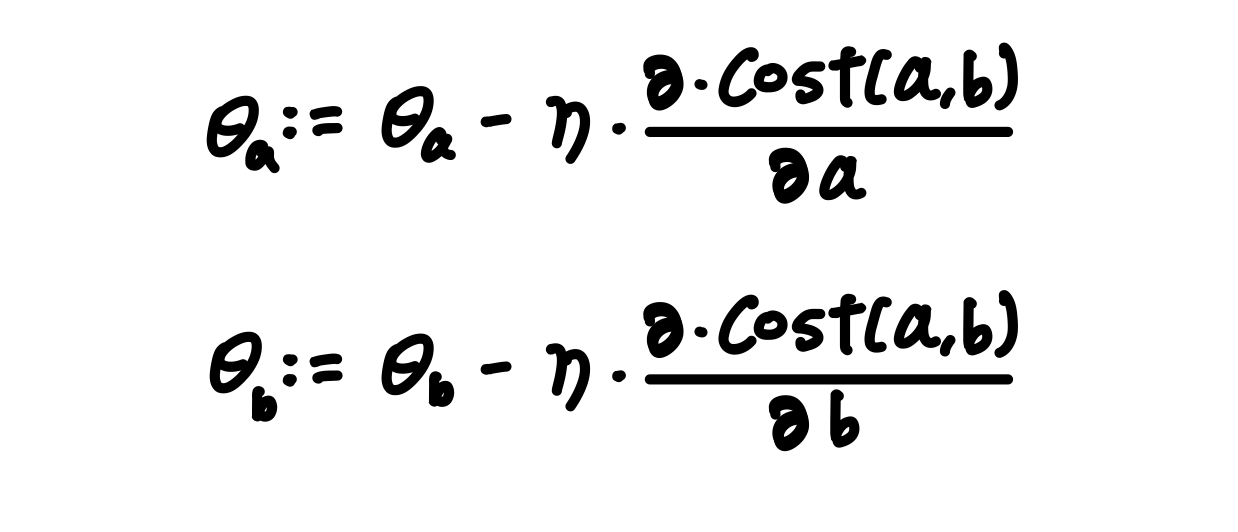
- 기존의 θ 에 (η x 편미분 한 값)을 빼준다.
(η: Learning Rate)
η: Learning Rate (학습률)
- 보폭을 결정한다. 주로 보폭을 줄이기 위해 0.1 ~ 0.0001 사이의 값을 준다.
- θ를 한번 Update할 때 보폭을 정하는 값이라고 생각하면 좋다.
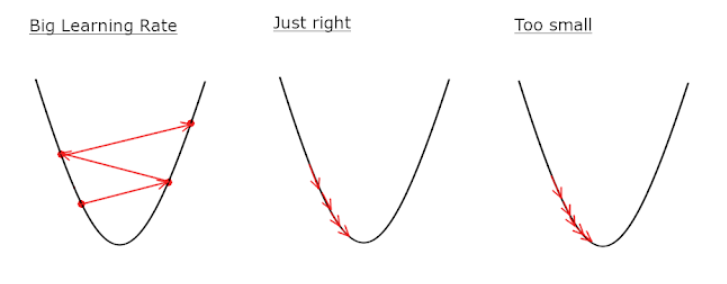
- Learning Rate가 너무 크면 Global Optimum으로 수렴하지 못하고 발산하게 된다.
- Learning Rate가 너무 작으면 Global Optimum에 수렴하는데 걸리는 시간이 너무 커져 연산에 있어서도 비효율 적이고, Local Optimum에서 고일 가능성이 있다.
- 따라서 적당한 값의 Learning Rate의 값을 찾아주어야 한다.

- 이 값이 θ(a) 보다 커지면 기울기는 음수값을 가져 반대방향으로 a를 Update한다.
- 즉, 여러 Iteration을 거치면 자동으로 기울기는 0으로 수렴하게 된다.
6. 반복 Epoch (Iteration)
머신러닝에서 인공지능 모델을 반복적으로 학습시키는데, 이때 학습의 횟수를 Epoch(에포크)라고 한다.
- 즉 Epoch 만큼 반복해서 model의 파라미터 θ를 Update하는 것이다.
- Epoch이 커질 수록 훈련 데이터에 더 잘 근사하게 된다.
- 하지만 너무 훈련데이터에 Fitting 되어, 일반화 성능이 떨어지는 Over Fitting 문제가 발생할 수도 있다.
OverFitting & UnderFitting(과대, 과소 적합)
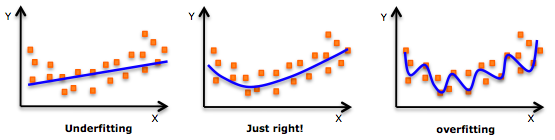
- OverFitting은 학습데이터에 너무 많이 Fitting되어,
새로운 테스트 데이터에 대해 일반화 성능을 내지 못하는 것을 의미한다. - UnderFitting은 학습데이터에 너무 적게 Fitting되어,
새로운 테스트 데이터에 대해 일반화 성능을 내지 못하는 것을 의미한다.
OverFitting & UnderFitting은 다음과 같은 상황에서 발생 가능하다.
<< OverFitting >>
- Epoch를 크게하여 모델을 너무 많이 학습시켰을 때
- 데이터에 비해 너무 무거운 모델을 사용하여, 모델 복잡도가 클 때
- BatchSize를 너무 작게하여, 작은 Batch 마다 너무 잦은 Update 할 때
<< UnderFitting >>
- 모델을 너무 적게 학습 시켰을 때
- 데이터에 비해 너무 가벼운 모델을 사용하여, 모델 복잡도가 작을 때
- 학습 데이터의 양이 너무 적을 때
