
SVM (서포트 벡터 머신)
1. 서포트 벡터 머신
서포트 벡터 머신은 대표적인 머신러닝 모델이다.
SVM은 SVR과 SVC로 나뉘는데, SVR은 회귀 모델이고 SVC는 분류모델이다.
하지만 통상적으로 SVM이라 하면, 주로 이진분류를 진행한다.
Binary Classification (이진 분류)
- 이진분류는 구분하려는 결과가 참 또는 거짓의 형태나, A 그룹 또는 B 그룹으로 데이터를 나누는 경우를 의미
ex) 사진이 개인지 고양이인지 분류, 영화 리뷰가 긍정인지 부정인지 판별 등
문제 정의
개와 고양이를 가장 잘 구분 짓는 직선 하나를 찾아보자!

다음 사진과 볼 수 있듯이, 우리는 이 데이터들을 기반으로 무한대에 가까운 다양한 선을 그을 수 있다.


하지만 어느 선이 개와 고양이를 가장 잘 분류하는지 알 수 없다.
따라서 새로운 데이터에 대해서 일반화 성능이 높은(잘 분류할 수 있는) 직선을 찾는 것이 목표이다.
그렇다면 어떻게 최적의 선을 찾을 수 있을까?
-> SVM 머신러닝 알고리즘을 통해 다음을 해결해보자
2. Decision Boundary
Hyper-Plane
서포트 벡터 머신은 두 클래스(개, 고양이)를 구분하기 위해 Decision Boundary, 즉 Hyper-Plane을 결정 짓는다.
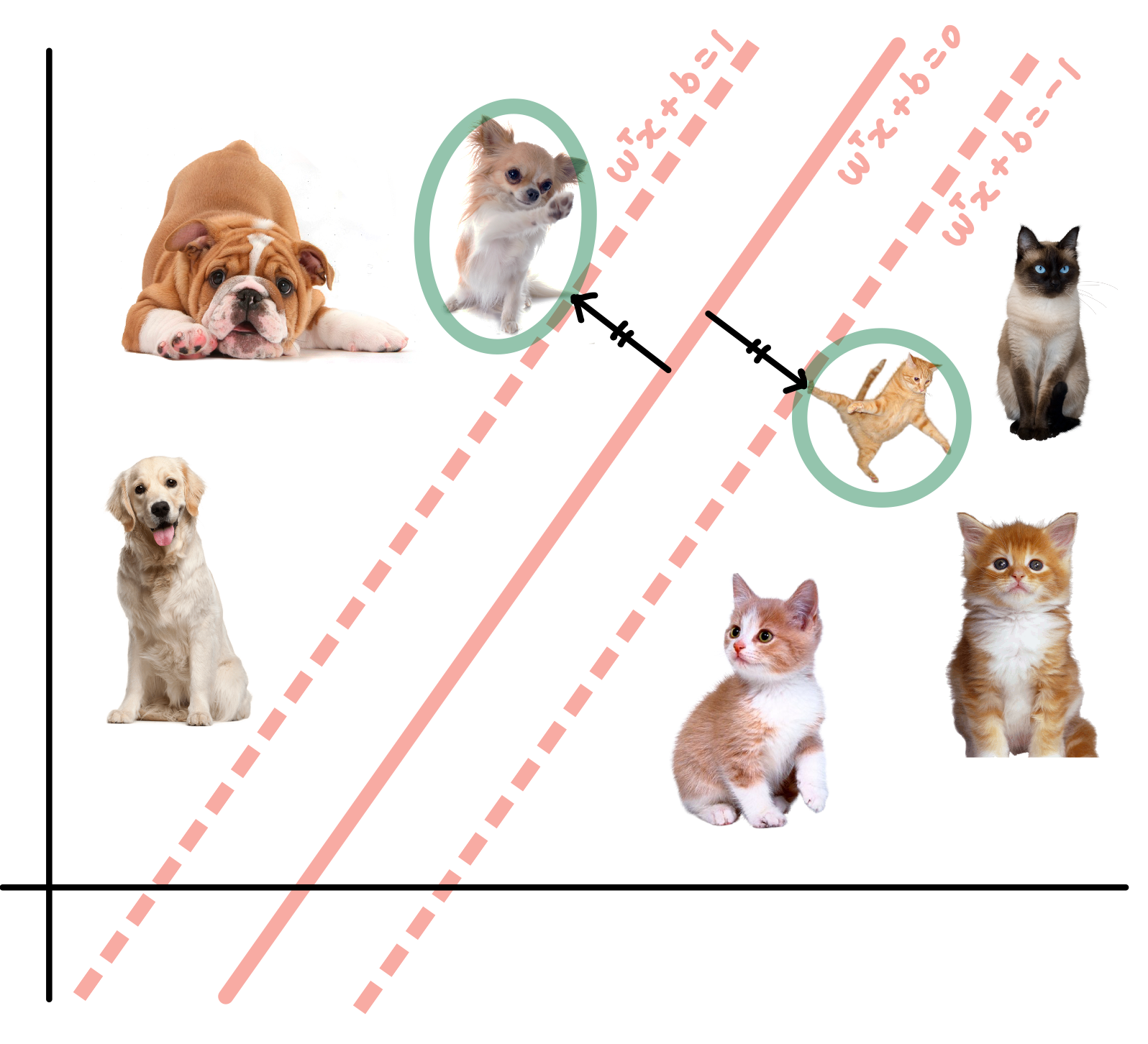
- 다음 사진에서 빨간 직선이 Hyper-Plane(Decision Boundary)이다.

SVM은 Hyper-Plane을 결정짓기 위해서 Margin을 최대화 한다.
Margin을 최대화한다고 했는데, 그럼 Margin은 무엇인가?
3. Margin
Margin은 Plus-Plane과 Minus-Plane 사이의 거리이다.
Plus-Plane은 치와와 강아지에 걸쳐있는 점선이고,
Minus-Plane은 고양이에 걸쳐있는 점선이다.
- Hyper Plane은 Plus-Plane과 Minus-Plane으로 부터 같은 거리에 결정된다.
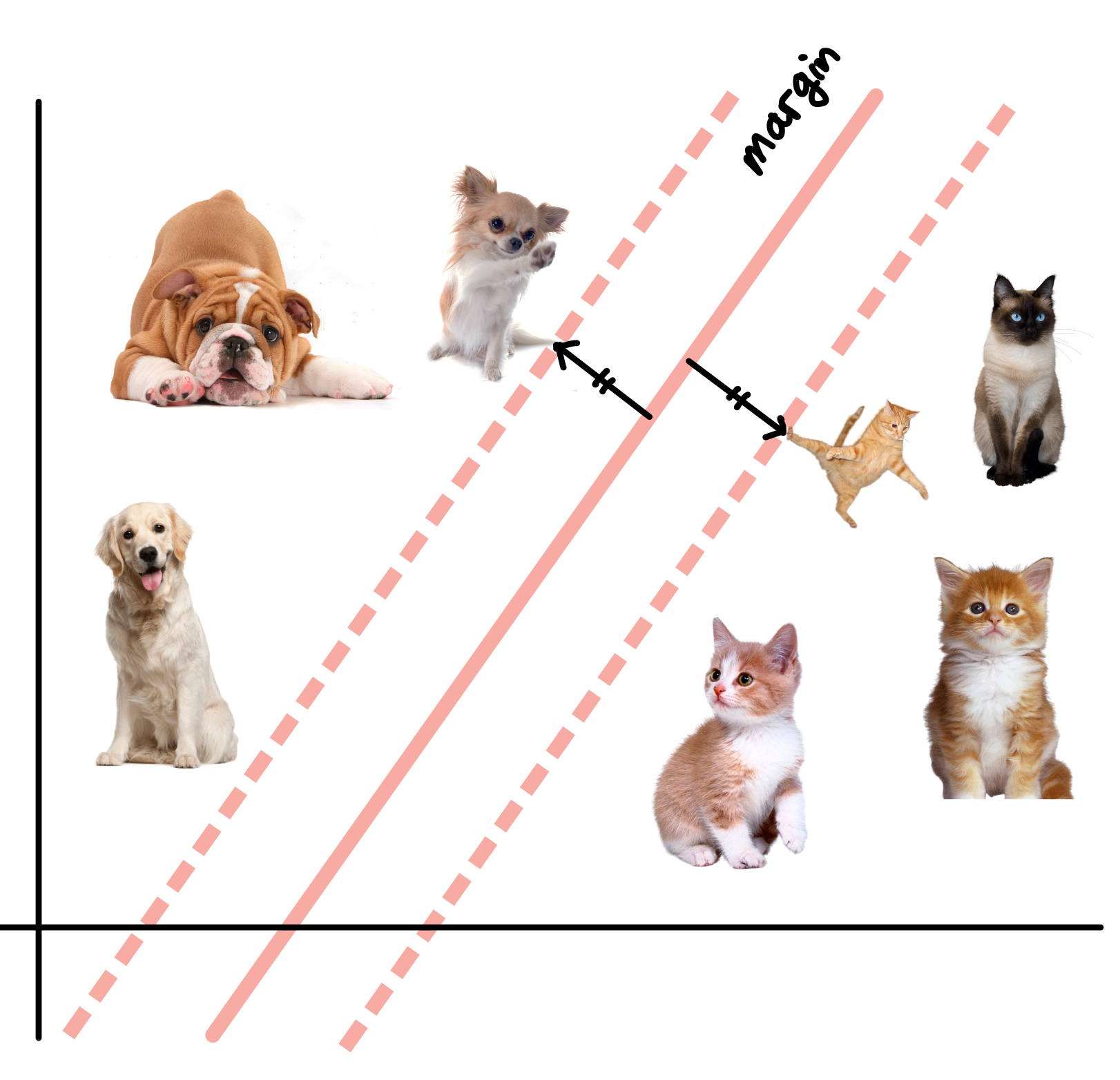
일반화 성능을 가장 잘 내는 직선을 찾기 위해서 마진을 최대화 해야한다고 했다.
그럼 마진을 결정짓는 요소를 보자.
Margin은 Plus-Plane과 Minus-Plane 사이의 거리인데,
- Plus-Plane을 결정 짓는 것은 다양한 개들 중에 치와와이고
- Minus-Plane을 결정 짓는 것은 하늘을 나는 고양이 사진이다.
즉 하늘을 나는 고양이와 치와와가 두 클래스를 전체를 대표해서 Hyper-Plane을 찾았다.
왜 많고 많은 데이터들 중에, 하늘을 나는 고양이와 치와와가 두 클래스의 대표가 되었을까?
-> Support Vector에 대해서 알아보자.
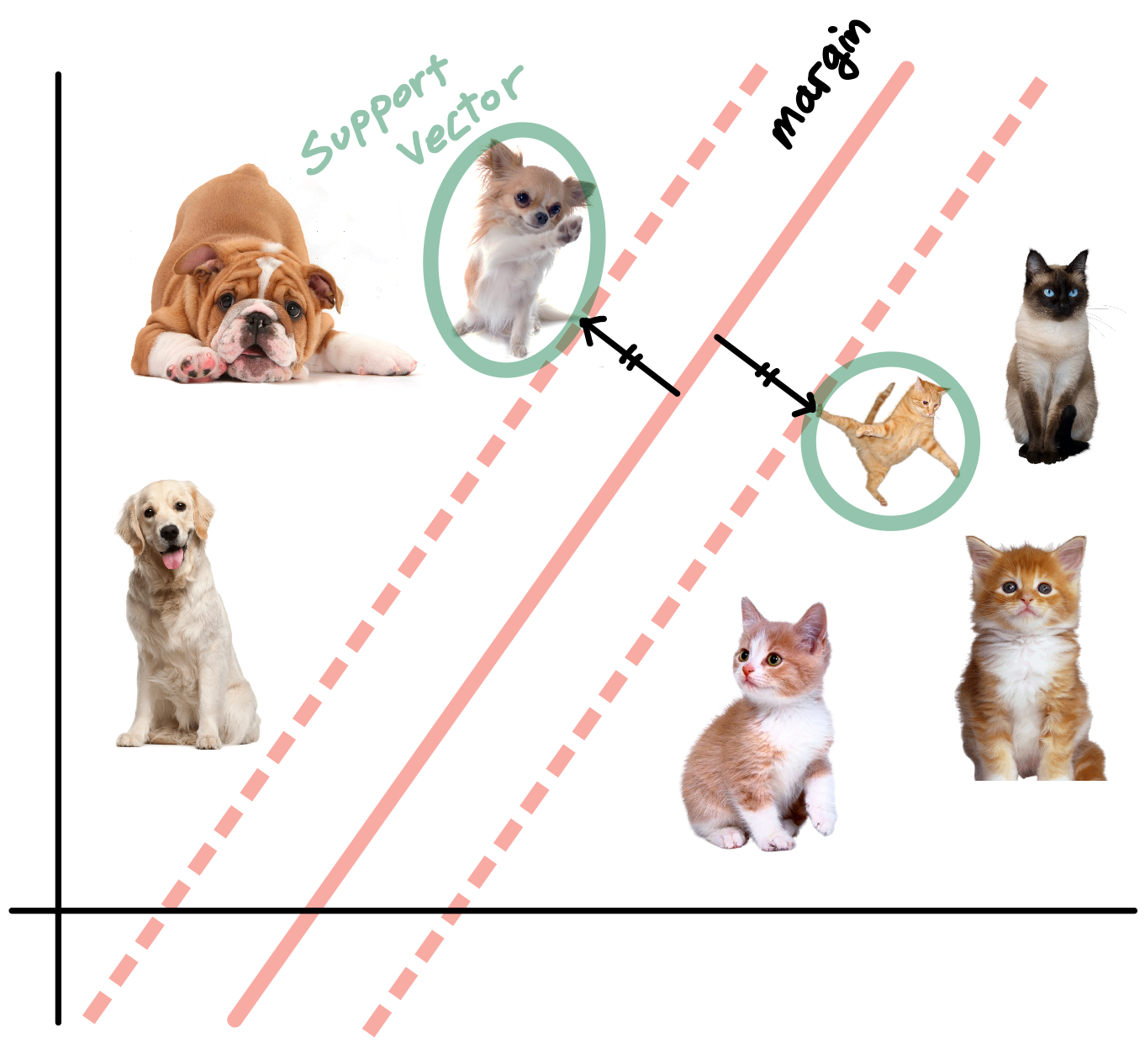
4. Support Vector (서포트 벡터)
서포트 벡터란 각각의 클래스를 대표하고, 마진을 형성하기 위한 Plus, Minus-Plane을 결정짓는데 필요한 데이터
Soft Margin
- 어느정도 오차를 허용해, 여유있게 서포트 벡터를 결정한다.
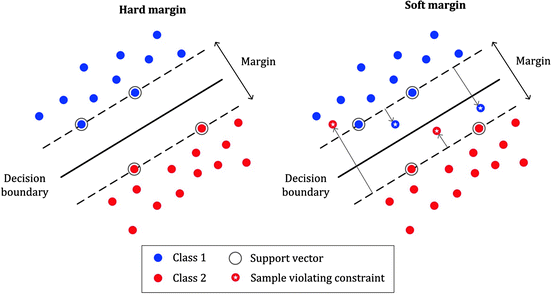
Hard Margin
- 어느 하나의 오차를 허용하지 않고, 타이트 하게 서포트 벡터를 결정한다.
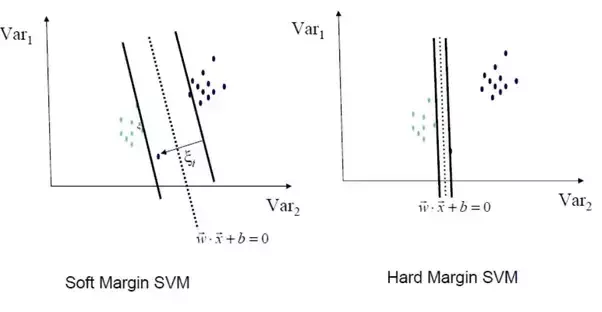
직선 w^T • x + b = 1을 만족하는 데이터 x와 w^T • x + b = -1을 만족하는 데이터 x가
Support Vector (서포트 벡터) 데이터가 된다.
SVM으로 Prediction을 하기 위해, 데이터 전체가 아닌 오직 서포트 벡터만 이용하기 때문에 연산량이 매우 적다.
w^T • x + b > 0 인 경우
- 양성 클래스인 개 클래스로 분류
w^T • x + b < 0 인 경우
- 음성 클래스인 고양이 클래스로 분류
5. 커널 트릭 (Kernel Trick)
Not Linearly Separable Data
개 고양이 데이터는 선형적으로 잘 분리되는 데이터였다.
하지만 대부분 Feature가 여러개이고, 선형적으로만 데이터가 존재하지 않는다.
따라서 SVM으로 Non-Linear Data를 Classification 하기 위해서는 커널을 이용해 차원을 변경시켜주어야 한다.
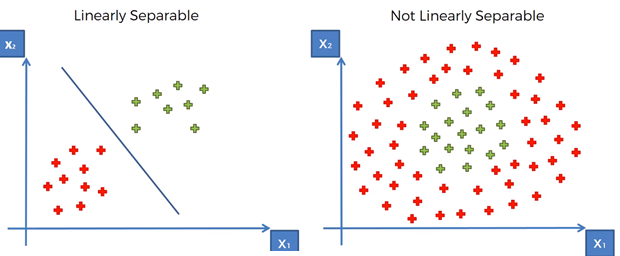
- 왼쪽 그림은 Linearly Separable한 데이터를 Classcification한 결과이고
- 오른쪽 그림은 Non Linearly Separable하기에 Classcification을 하지 못했다.
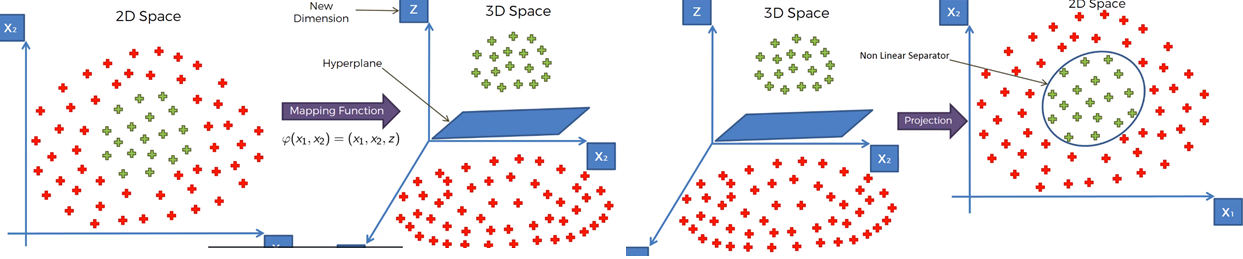
-> Not Linearly Separable한 데이터는 Hyper-Plane을 찾을 수 없다.
따라서 2D data를 3D로 차원을 변경시켜주면 Hyper-Plane을 찾을 수 있다.
(Kernel Trick)
출처
https://medium.com/pursuitnotes/day-12-kernel-svm-non-linear-svm-5fdefe77836c
https://yngie-c.github.io/machine%20learning/2020/04/26/SVM/
