2.4 통계 기반 기법 개선하기

2.4.1 상호정보량

동시발생 행렬의 원소 : 두 단어가 동시에 발생한 횟수

ex. the, car, drive

• the + car : 동시발생 횟수 많음, 연관성 적음
• car + drive : 동시발생 횟수 적음, 연관성 높음

Error! 관사와 같은 연관성 적은 단어가 동시발생 횟수만으로 연관성이 높다고 측정될 수 있음

점별 상호정보량 (PMI)

1. 확률로 나타낼 경우

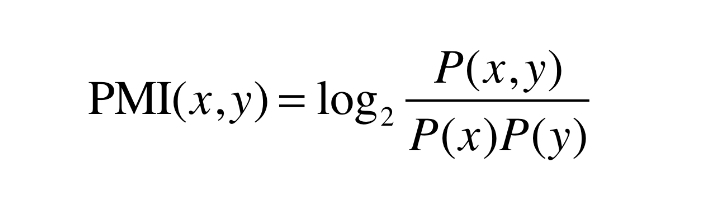
P(x) : x가 일어날 확률

• 단어 x가 말뭉치 안에 등장할 확률
  ex. P(x) = 100/10000

P(Y) : y가 일어날 확률

• 단어 y가 말뭉치 안에 등장할 확률

P(x, y) : x, y가 동시에 일어날 확률

• 단어 x, y가 말뭉치 안에 등장할 확률
  ex. P(x, y) = 10/10000

PMI가 높을수록 관련성이 높음

2. 행렬로 나타낼 경우

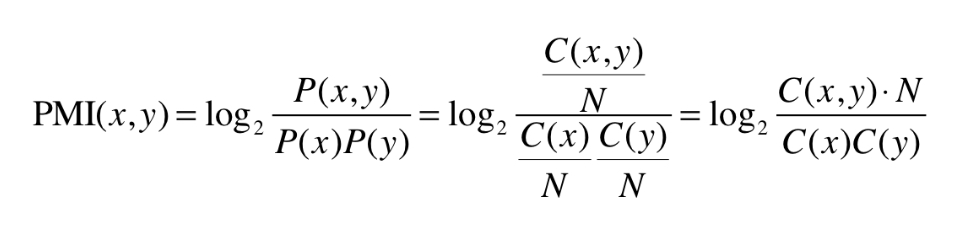
N : 말뭉치에 포함된 단어 수
C : 동시발생 행렬
C(x) : 말뭉치에 단어 x의 등장 횟수
C(y) : 말뭉치에 단어 y의 등장 횟수
C(x, y) : 말뭉치에 단어 x와 y가 동시발생하는 횟수

ex. N = 10000, 'the' = 1000, 'car' = 20, 'drive' = 10

• 동시발생 횟수 관점
  'the' + 'car' = 10
  'car' + 'drive' = 5
  -> 'the'와 'car'이 'car'과 'drive'보다 연관성이 높다고 나옴
• PMI 관점
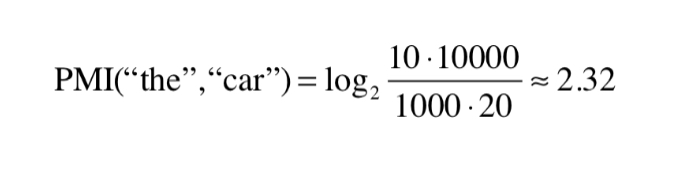
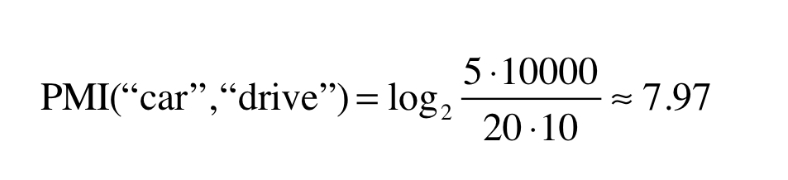  -> 'the'와 'car'이 'car'과 'drive'보다 연관성이 낮다고 나옴

단어가 단독으로 출현하는 횟수가 고려되었으므로, 출현 횟수보다 관련성에 PMI 척도가 치중됨

양의 상호정보량 (PPMI)

: 단어 사이의 관련성을 0 이상의 실수로 나타낸 상호 정보량

• 두 단어의 동시발생 횟수가 0일 경우, log값이 -무한대로 가는 문제점 해결
• PMI가 음수일경우, 0으로 취급함
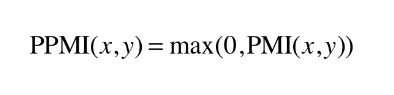
• 동시발생 행렬을 PPMI 행렬로 변환하는 함수

def ppmi(C, verbose=False, eps=1e-8):
	M = np.zeros_like(C, dtype=np.float32)
    N = np.sum(C)
    S = np.sum(C, axis=0)
    total = C.shape[0] * C.shpae[1]
    cnt = 0
    
    for i in range(C.shape[0]):
    	for j in range(C.shape[1]):
         pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
         M[i, j] = max(0, pmi)
         
         if verbose:
         	cnt += 1
            if cnt % (total/100) == 0:
            	print('%.1f%% 완료' % (100*cnt/total))
    return M

• C : 동시발생 행렬
  C[i, j] : C(x, y), x와 y의 동시발생 행렬
  S[i] : x 발생 횟수
  S[j] : y 발생 횟수
• N : 전체 단어 수
• verbose : 진행상황 출력 여부
  verbose=True : 중간 진행 상황 확인 가능

작은 값 eps를 사용하여 log0이 -무한대가 되는 상황을 방지함

Example Code

# coding: utf-8
import sys
sys.path.append('..')
import numpy as np
from common.util import preprocess, create_co_matrix, cos_similarity, ppmi


text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
W = ppmi(C)

np.set_printoptions(precision=3)  # 유효 자릿수를 세 자리로 표시
print('동시발생 행렬')
print(C)
print('-'*50)
print('PPMI')
print(W)

실행 결과

PMI의 문제점

1. 벡터의 차원 수 증가
   -> 말뭉치의 어휘 수가 증가함에 따라 각 단어 벡터이 차원 수도 증가함

2. 행렬의 원소 대부분이 0
   -> 벡터의 각 원소의 중요도가 결여됨 (노이즈에 약하고 견고하지 못함)

Solve! 벡터의 차원 감소

2.4.2 차원 감소

차원 감소 (Dimensionality Reduction)

: 벡터의 차원을 줄이는 방법

• 중요한 정보는 최대한 유지하면서 줄여야함

특이값 분해 (SVD)

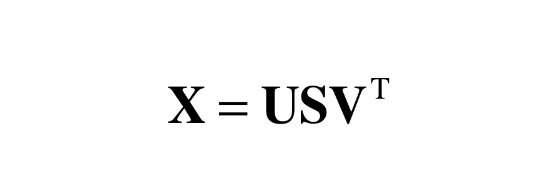임의의 행렬 X를 세 행렬의 곱으로 분해함

• U : 직교행렬
• V : 직교행렬
• S : 대각행렬

U = 단어 공간, S = 특이값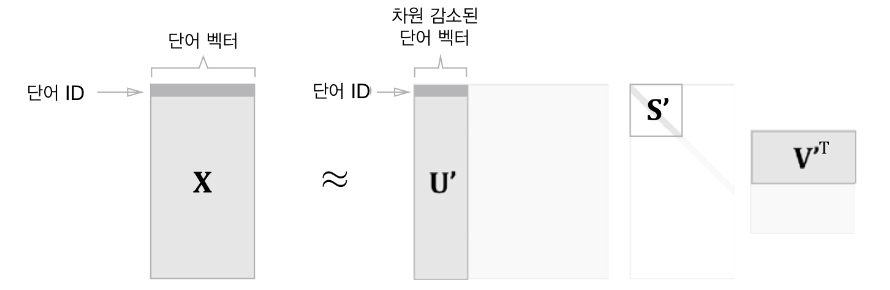 S가 작다면, U에서 여분의 열벡터를 축소하여 원래의 행렬에 근사시킬 수 있음

PPMI 행렬을 적용하면, 행렬 X의 각 행에 해당하는 ID의 단어 벡터가 저장되어 있으며, 그 단어 벡터가 행렬 U라는 차원 감소된 벡터로 표현됨

2.4.3 SVD에 의한 차원 감소

SVD code

numpy의 linalg 모듈을 사용해 svd 메소드 실행 가능

import numpy as np

np.linalg.svd

Example code #1

# coding: utf-8
import sys
sys.path.append('..')
import numpy as np
import matplotlib.pyplot as plt
from common.util import preprocess, create_co_matrix, ppmi


text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(id_to_word)
C = create_co_matrix(corpus, vocab_size, window_size=1)
W = ppmi(C)

# SVD
U, S, V = np.linalg.svd(W)

np.set_printoptions(precision=3)  # 유효 자릿수를 세 자리로 표시
print(C[0]) # 동시발생 행렬
print(W[0]) # PPMI 행렬, 희소 벡터
print(U[0]) # SVD, 밀집 벡터
print(U[0, :2]) # 2차원으로 감소
 
# plot
for word, word_id in word_to_id.items():
    plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:,0], U[:,1], alpha=0.5)
plt.show()

실행 결과

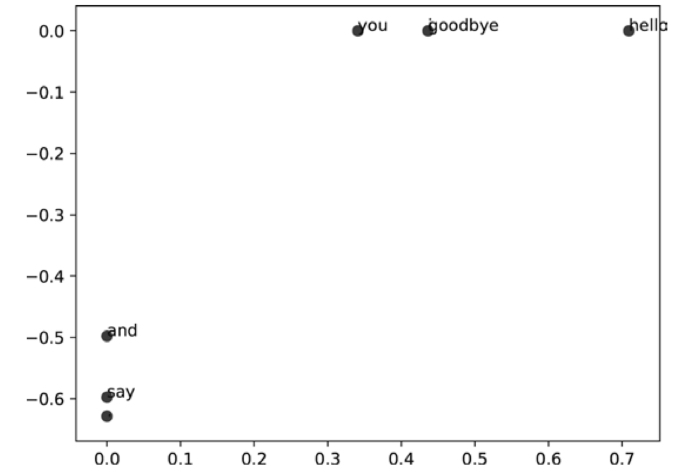
• 'goodbye' + 'hello'
• 'you' + 'i'

Try! SVD의 시간 복잡도는 O(N3)이므로 Truncated SVD를 이용해 속도를 향상시켜보자!

Truncated SVD
: 특잇값이 작은 것을 버리는 방식으로 성능 향상

• scikit-learn 라이브러리

Try! 성능을 높이기위해 PTB 데이터셋을 이용해보자!

PTB 데이터셋
: 보다 큰 말뭉치

• Tomas Mikolov의 web page에서 다운 가능

2.4.4 PTB 데이터셋

펜 트리뱅크 (PTB)

: 큰 말뭉치

• 한 문장이 하나의 줄로 저장되어 있음
  

Example code

# coding: utf-8
import sys
sys.path.append('..')
from dataset import ptb


corpus, word_to_id, id_to_word = ptb.load_data('train')

print('말뭉치 크기:', len(corpus))
print('corpus[:30]:', corpus[:30])
print()
print('id_to_word[0]:', id_to_word[0])
print('id_to_word[1]:', id_to_word[1])
print('id_to_word[2]:', id_to_word[2])
print()
print("word_to_id['car']:", word_to_id['car'])
print("word_to_id['happy']:", word_to_id['happy'])
print("word_to_id['lexus']:", word_to_id['lexus'])

• corpus : 단어 ID 목록
• id_to_word : 단어 ID에서 단어로 변환하는 딕셔너리
• word_to_id : 단어에서 단어 ID로 변환하는 딕셔너리
• ptb.load_data() : 데이터 읽기

실행 결과

2.4.5 PTD 데이터셋 평가

Try! PTB 데이터셋에 통계 기반 기법을 적용해보자!

Example code

# coding: utf-8
import sys
sys.path.append('..')
import numpy as np
from common.util import most_similar, create_co_matrix, ppmi
from dataset import ptb


window_size = 2
wordvec_size = 100

corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)
print('동시발생 수 계산 ...')
C = create_co_matrix(corpus, vocab_size, window_size)
print('PPMI 계산 ...')
W = ppmi(C, verbose=True)

print('calculating SVD ...')
try:
    # truncated SVD (빠르다!)
    from sklearn.utils.extmath import randomized_svd
    U, S, V = randomized_svd(W, n_components=wordvec_size, n_iter=5,
                             random_state=None)
except ImportError:
    # SVD (느리다)
    U, S, V = np.linalg.svd(W)

word_vecs = U[:, :wordvec_size]

querys = ['you', 'year', 'car', 'toyota']
for query in querys:
    most_similar(query, word_to_id, id_to_word, word_vecs, top=5)

• randomized_svd() : 무작위 수를 이용한 Truncated SVD
  (특이값이 큰 것들만 계산함)
  (기본적인 SVD보다 빠름)

실행 결과

• 무작위 수를 사용하므로 결과가 매번 다름

단어의 의미 혹은 문법적인 관점에서 비슷한 단어들이 가까운 벡터로 나타남
Solve! 단어의 의미를 벡터로 잘 인코딩함

2.5 정리

1. 말뭉치 속 단어의 등장 횟수를 세어 PPMI 행렬로 변환함
2. SVD를 이용해 차원을 감소시킴
3. 각 단어의 분산 표현을 만들어냄
4. 의미가 비슷한 단어들이 벡터 공간에서도 서로 가까이 모여있음을 확인함
5. 각 단어가 고정 길이의 밀집 벡터로 표현됨
6. 대규모 말뭉치를 사용하면 단어의 분산 표현의 품질이 좋아짐