10. 정렬(Sorting)

deepTree·2024년 11월 28일

목록 보기

7/9

이 내용은 윤성우의 열혈 자료구조를 학습한 내용입니다.

1. 단순한 정렬 알고리즘

1-1. 버블 정렬의 이해와 구현

버블 정렬(Bubble Sort)
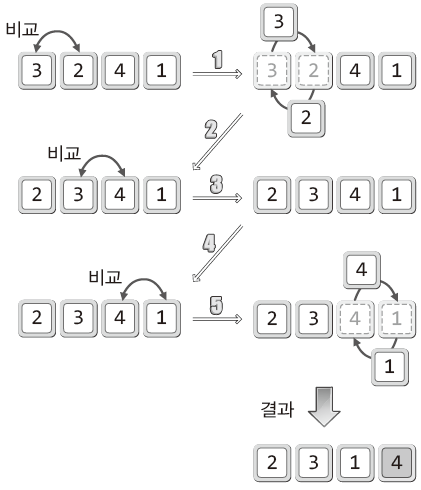
- 인접한 두 개의 데이터를 비교해가면서 정렬을 진행하는 방식

🔻 구현: 오름차순 기준

정렬의 우선순위가 가장 낮은, 가장 큰 값을 맨 뒤로 보낸다.
- 정렬이 완료된 데이터를 제외하고 위 과정을 반복한다.

코드

#include <stdio.h>

void BubbleSort(int arr[], int n)
{
	int i, j;
	int temp;

	for(i=0; i<n-1; i++)
	{
		for(j=0; j<(n-i)-1; j++)
		{
			if(arr[j] > arr[j+1]) // 오름차순 정렬
			{
				/* 데이터의 교환 */
				temp = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = temp;
			}
		}
	}
}

int main(void)
{
	int arr[4] = {3, 2, 4, 1};
	int i;

	BubbleSort(arr, sizeof(arr)/sizeof(int));

	for(i=0; i<4; i++)
		printf("%d ", arr[i]); // 1 2 3 4

	printf("\n");
	return 0;
}

간단히 이중 for문을 활용해서 구현할 수 있다.

🔻 성능평가

핵심 연산
- 비교연산: 두 데이터간 비교연산의 횟수
- 대입연산(데이터의 이동): 위치의 변경을 위한 데이터의 이동횟수

→ 실제로 빅-오를 결정하는 기준은 ‘비교의 횟수’이다. (배열의 끝까지 확인해야 하므로)

시간복잡도: 정렬대상 n개 기준
연산 최악 최선
비교연산 $O(n^2)$ $O(n^2)$
대입연산 $O(n^2)$ $0$
- 대입연산의 경우, 데이터가 정렬된 상태면 교환이 한 번도 일어나지 않는다.

연산	최악	최선
비교연산	$O(n^2)$	$O(n^2)$
대입연산	$O(n^2)$	$0$

1-2. 선택 정렬의 이해와 구현

선택 정렬(Selection Sort)
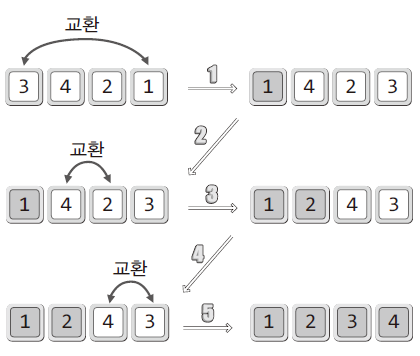
- 정렬순서에 맞게 하나씩 선택해서 옮기는, 옮기면서 정렬이 되게 하는 알고리즘

🔻 구현: 오름차순 기준

정렬순서상 가장 앞서는 것을 선택해서 가장 왼쪽으로 이동시키고, 원래 그 자리에 있던 데이터는 빈 자리에 가져다 놓는다.

코드

#include <stdio.h>

void SelSort(int arr[], int n)
{
	int i, j;
	int maxIdx;
	int temp;

	for(i=0; i<n-1; i++)
	{
		maxIdx = i; // 현재 탐색 구간 중 최댓값을 가지는 인덱스

		for(j=i+1; j<n; j++)   // 최솟값 탐색
		{
			if(arr[j] < arr[maxIdx])
				maxIdx = j;
		}

		/* 데이터 교환 */
		temp = arr[i];
		arr[i] = arr[maxIdx];
		arr[maxIdx] = temp;
	}
}

🔻 성능평가

시간복잡도: 정렬대상 n개 기준
연산 최악 최선
비교연산 $O(n^2)$ $O(n^2)$
대입연산 $O(n)$ $O(n)$

연산	최악	최선
비교연산	$O(n^2)$	$O(n^2)$
대입연산	$O(n)$	$O(n)$

1-3. 삽입 정렬의 이해와 구현

삽입 정렬(Insertion Sort)
- 정렬 대상을 두 부분으로 나눠서, 정렬 안 된 부분에 있는 데이터를 정렬된 부분의 특정 위치에 ‘삽입’해 가면서 정렬을 진행하는 알고리즘

🔻 구현

정렬 안 된 부분에 있는 데이터를 정렬된 부분의 특정 위치에 삽입한다.
- 정렬이 완료된 영역의 다음에 위치한 데이터가 그 다음 정렬대상이다.
- 데이터를 한 칸씩 뒤로 밀면서 삽입할 위치를 찾는다.

코드

#include <stdio.h>

void InserSort(int arr[], int n)
{
	int i, j;
	int insData;

	for(i=1; i<n; i++)
	{
		insData = arr[i];   // 정렬대상을 insData에 저장

		for(j=i-1; j>=0 ; j--)
		{
			if(arr[j] > insData) 
				arr[j+1] = arr[j];    // 비교대상 한 칸 뒤로 밀기
			else
				break;   // 삽입 위치 결정 및 탈출
		}

		arr[j+1] = insData;  // 데이터 삽입
	}
}

🔻 성능평가

삽입 정렬은 정렬대상의 대부분이 이미 정렬된 경우 매우 빠르게 동작한다.
시간복잡도: 정렬대상 n개 기준
- 최악: $O(n^2)$
- 최선: $0$ (데이터가 완전히 정렬된 상태)

2. 복잡하지만 효율적인 정렬 알고리즘

2-1. 힙 정렬의 이해와 구현

힙 정렬(Heap Sort)
- 힙의 특성을 활용하여 정렬하는 알고리즘
  - 힙의 루트 노드에 저장된 값이 정렬순서상 가장 앞선다.

🔻 구현

코드

#include <stdio.h>
#include "UsefulHeap.h"

int PriComp(int n1, int n2)
{
	return n2-n1; // 오름차순 정렬
	// return n1-n2; // 내림차순 정렬
}

void HeapSort(int arr[], int n, PriorityComp pc)
{
	Heap heap;
	int i;

	HeapInit(&heap, pc);

	// 데이터를 모두 힙에 넣는다.
	for(i=0; i<n; i++)
		HInsert(&heap, arr[i]);

	// 힙에서 다시 데이터를 꺼낸다.
	for(i=0; i<n; i++)
		arr[i] = HDelete(&heap);
}

이전 글에서 작성한 힙의 헤더, 소스 파일을 활용한다.
단순히 힙을 활용하여 힙에 데이터를 넣고, 꺼낸 값을 배열에 저장해 완성한다.
- 꺼낼 때 힙의 루트 노드(가장 작은)에 저장된 데이터가 반환된다.

🔻 성능평가

힙의 시간복잡도
- 데이터 저장: $O(log_2n)$
- 데이터 삭제: $O(log_2n)$
힙 정렬의 시간 복잡도: 정렬대상 n개 기준
- $O(nlog_2n)$

2-2. 병합 정렬의 이해와 구현

분할 정복(divide and conquer)
- 복잡한 문제를 복잡하지 않은 문제로 ‘분할’하여 ‘정복’하는 방법
1. 분할: 해결이 용이한 단계까지 문제를 분할
2. 정복: 해결이 용이한 수준까지 분할된 문제를 해결
3. 결합: 분할해서 해결한 결과를 결합하여 마무리
병합 정렬(Merge Sort)
- ‘분할 정복’이라는 알고리즘 디자인 기법에 근거하여 만들어진 정렬 방법
- n개의 데이터를 동시에 정렬하는 것보다, 이를 둘로 나눠서 n/2 개의 데이터를 정렬하는 것이 더 쉽다.

✔️ 기본 원리

실제 정렬은 나눈 것을 ‘병합’하는 과정에서 이뤄진다.

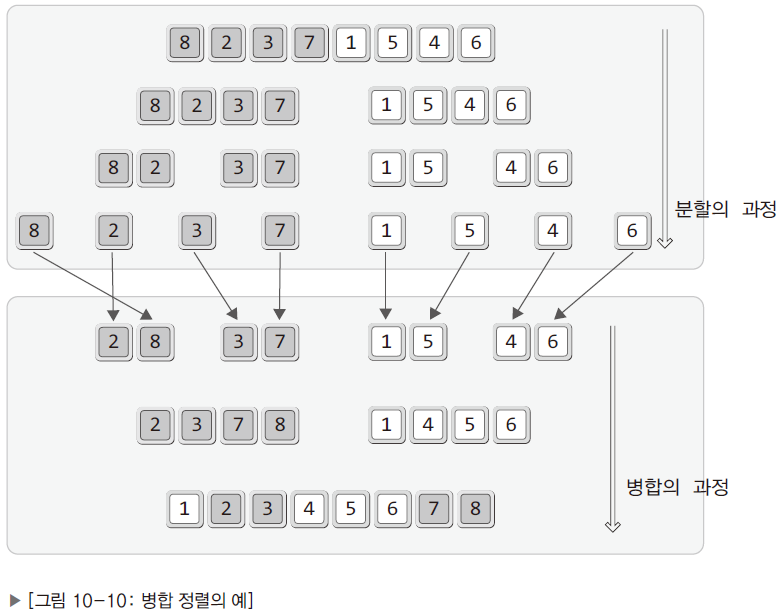
병합정렬의예

분할
- 병합 정렬은 데이터가 1개 남을 때까지 분할을 해나간다.
- 분할의 과정은 재귀적이다. (반으로 나눈다)
병합
- 정렬순서를 고려해서 묶는다.

🔻 구현

코드

#include <stdio.h>
#include <stdlib.h>

void MergeTwoArea(int arr[], int left, int mid, int right)
{
	int fIdx = left; // 앞쪽 구역 인덱스
	int rIdx = mid+1; // 뒤쪽 구역 인덱스
	int i;

	// 병합한 결과를 담을 배열 sortArr 동적할당
	int * sortArr = (int*)malloc(sizeof(int)*(right+1));
	int sIdx = left; // sortArr의 인덱스

	while(fIdx<=mid && rIdx<=right)
	{
		// 병합할 두 영역의 데이터들을 비교하여
		// 정렬순서대로 sortArr에 하나씩 옮긴다.
		if(arr[fIdx] <= arr[rIdx])
			sortArr[sIdx] = arr[fIdx++];
		else
			sortArr[sIdx] = arr[rIdx++];

		sIdx++;
	}

	if(fIdx > mid)	// 배열의 앞부분이 모두 sortArr에 옮겨졌다면
	{
		// 배열의 뒷부분에 남은 데이터들을 sortArr에 그대로 옮긴다.
		for(i=rIdx; i<=right; i++, sIdx++)
			sortArr[sIdx] = arr[i];
	}
	else	// 배열의 뒷부분이 모두 sortArr에 옮겨졌다면
	{
		// 배열의 앞부분에 남은 데이터들을 sortArr에 그대로 옮긴다.
		for(i=fIdx; i<=mid; i++, sIdx++)
			sortArr[sIdx] = arr[i];	
	}

	for(i=left; i<=right; i++)
		arr[i] = sortArr[i];
	
	free(sortArr);
}

void MergeSort(int arr[], int left, int right)
{
	int mid;

	if(left < right) // 더 나눌 수 있다.
	{
		// 중간 지점을 계산
		mid = (left+right) / 2;

		// 둘로 나눠서 각각을 정렬
		MergeSort(arr, left, mid); // left-mid에 위치한 데이터 정렬
		MergeSort(arr, mid+1, right); // mid+1-right에 위치한 데이터 정렬

		// 정렬된 두 배열 병합
		MergeTwoArea(arr, left, mid, right);
	}
}

void MergeSort(int arr[], int left, int right);
- 재귀적으로 분할하고, 분할된 배열을 병합하는 함수를 호출한다.
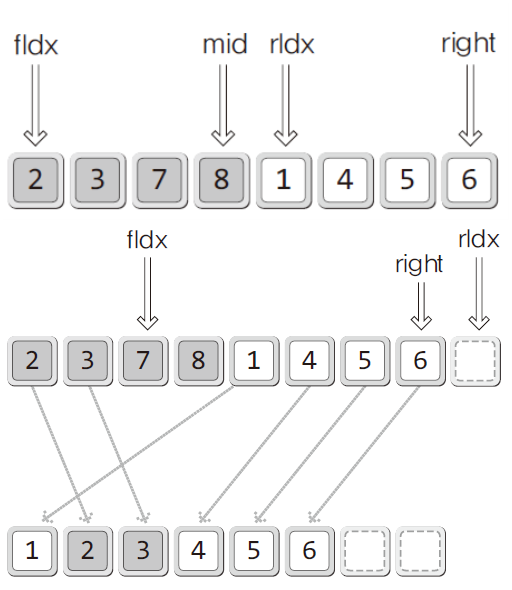
void MergeTwoArea(int arr[], int left, int mid, int right);
- 병합결과를 담을 배열을 선언하고 분할된 두 영역의 값들을 순서대로 비교해서 담는다.
- 병합결과를 실제 배열에 적용한다.

🔻 성능평가

시간복잡도: 정렬대상 n개 기준
- 비교연산: $O(nlog_2n)$
- 이동연산: $O(nlog_2n)$
단점: 정렬 대상이 배열일 경우 임시 메모리가 필요하다.

2-3. 퀵 정렬의 이해와 구현

퀵 정렬(Quick Sort)
- ‘분할 정복’에 근거하여 만들어진 정렬 방법

✔️ 기본 원리

퀵 정렬의 초기화
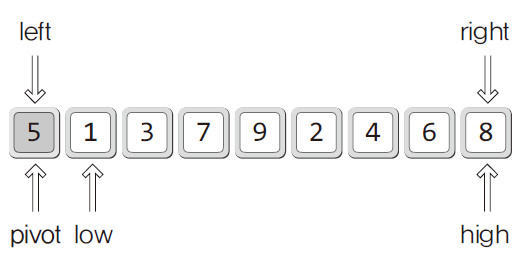
- left: 정렬대상의 가장 왼쪽 지점
- right: 정렬대상의 가장 오른쪽 지점
- pivot: 기준
  - 가장 왼쪽에 위치한 데이터를 퀵 정렬에 필요한 피벗으로 정한다.
- low: 피벗을 제외한 가장 왼쪽에 위치한 지점
- high: 피벗을 제외한 가장 오른쪽에 위치한 지점

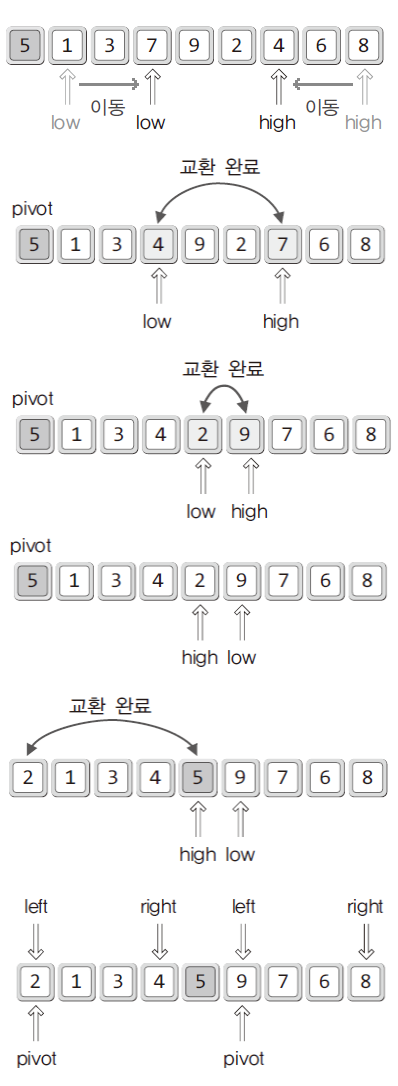
퀵 정렬의 이동(low와 high의 이동): 오름차순 기준
- low: 피벗보다 정렬의 우선순위가 낮은(큰 값) 데이터를 만날 때까지
- high: 피벗보다 정렬의 우선순위가 높은(작은 값) 데이터를 만날 때까지
퀵 정렬의 교환(low와 high의 교환)
- low와 high의 이동이 멈췄을 때 두 위치의 데이터를 교환한다.
- low > high 일 때까지, 이동을 진행한다.
📌 퀵정렬의 이동(pivot의 이동)
- 위치가 교차되면 pivot과 high가 가리키는 데이터를 서로 교환한다.
- 피벗의 왼편에는 피벗보다 작은 값, 오른편에는 피벗보다 큰 값들이 위치한다.
left > right 일 때까지, 두 개의 영역으로 나누어 1 ~ 3 과정을 반복한다.

퀵정렬

🔻 구현

코드

#include <stdio.h>

void Swap(int arr[], int idx1, int idx2)
{
	int temp = arr[idx1];
	arr[idx1] = arr[idx2];
	arr[idx2] = temp;
}

int Partition(int arr[], int left, int right)
{
	int pivot = arr[left];    // 피벗의 위치는 가장 왼쪽
	int low = left+1;
	int high = right;

	while(low <= high)    // 교차되지 않을 때까지 반복
	{
		// low와 high 이동	
		while(pivot >= arr[low] && low <= right)
			low++;

		while(pivot <= arr[high] && high >= (left+1))
			high--;

		if(low <= high)    // 교차되지 않은 상태라면 swap 실행
			Swap(arr, low, high);
	}

	Swap(arr, left, high);    // 피벗과 high가 가리키는 대상 교환
	return high;    // 옮겨진 피벗의 위치정보 반환
}

void QuickSort(int arr[], int left, int right)
{
	if(left <= right)
	{
		int pivot = Partition(arr, left, right);    // 둘로 나눠서
		QuickSort(arr, left, pivot-1);    // 왼쪽 영역 정렬
		QuickSort(arr, pivot+1, right);    // 오른쪽 영역 정렬
	}
}

void QuickSort(int arr[], int left, int right);
- 피봇 기준으로 영역을 둘로 나눠서 정렬 진행
void Swap(int arr[], int idx1, int idx2); : 값 교환
int Partition(int arr[], int left, int right); : 정렬 진행

🚩 피봇의 선택: 피봇이 중간에 해당하는 값일 경우, 정렬대상은 균등하게 나뉜다.

Partition 함수의 호출횟수(정렬 과정에서 선택되는 피벗의 수)가 감소한다.

🔻 성능평가

시간복잡도: 정렬대상 n개 기준
- 임의의 탐색구간에서 비교연산의 횟수는 n 개이다. (low와 high의 값을 pivot과 비교)
- 최선: $O(nlog_2n)$
  - ‘중간에 가까운 피벗을 선택’함으로써 최선의 경우에 가까운 성능을 평균적으로 보인다.
  - 다른 정렬 알고리즘과 비교했을 때에도 평균적으로 가장 빠른 것으로 알려져 있다.
- 최악: $O(n^2)$
  - 모든 데이터가 이미 정렬되어 있는 상태 + 피벗이 가장 작은 값

2-4. 기수 정렬의 이해

기수 정렬(Radix Sort)
- 데이터를 구성하는 기본 요소(기수)를 이용해서 정렬을 진행하는 방식
- 정렬 순서상 앞서고 뒤섬의 판단을 위한 비교연산을 하지 않는다.
- 정렬 알고리즘의 한계로 알려진 $O(nlog_2n)$ 을 뛰어 넘을 수 있다.
- ‘데이터의 길이’가 같은 데이터들을 대상으로만 정렬이 가능하다.

✔️ 기본 원리
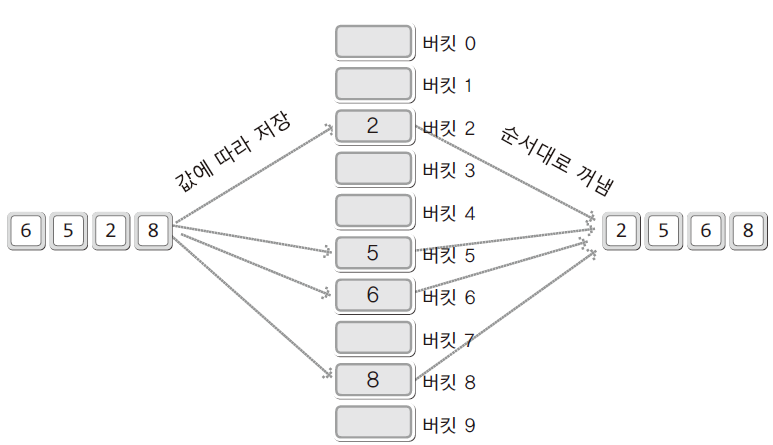
기수정렬원리

정렬대상을 값에 해당하는 버킷으로 이동시키고, 이동이 끝났다면 순서대로 값을 꺼내서 차례로 나열한다.

기수(radix): 주어진 데이터를 구성하는 기본 요소(기호)
- Ex. 10진수의 경우, 0 ~ 9 까지의 숫자
버킷(bucket): 기수의 수에 해당하는 만큼의 버킷을 활용한다.

🚩 LSD 기수 정렬

LSD(Least Significant Digit)
- ‘덜 중요한 자릿수’에서부터 정렬을 진행해 나간다.

정렬과정
1. 첫 번째 자릿수(덜 중요한 자릿수)를 기준으로 하여 버킷에 값을 넣는다.
  - 대소 비교에 가장 영향력이 작은 자릿수부터 비교를 한다.
2. 버킷 0에서부터 시작해서 데이터를 꺼낸다.
  - 하나의 버킷에 둘 이상의 데이터가 존재하는 경우 들어간 순서대로 꺼낸다.
3. 자릿수를 바꾸어 1 ~ 2 과정을 반복한다.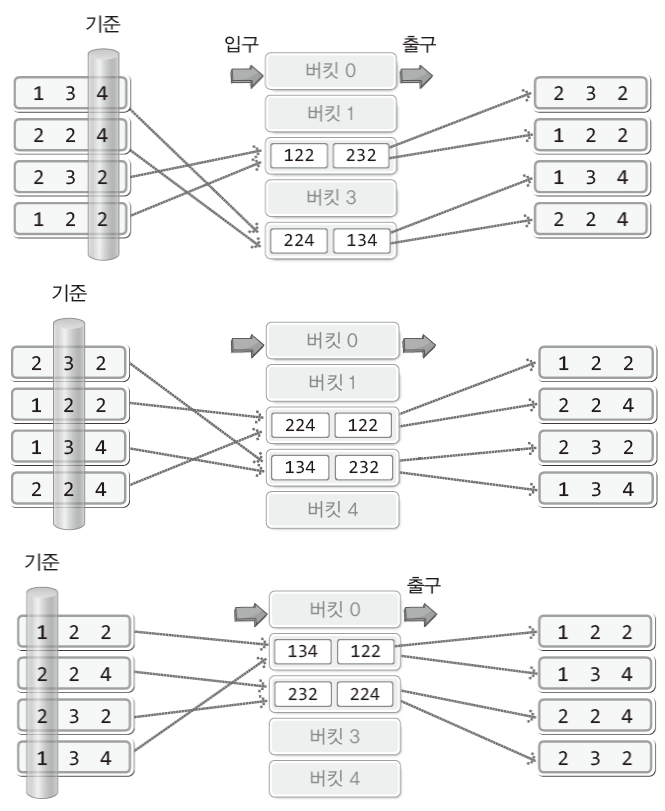

✅ 기수 정렬: LSD vs MSD

MSD(Most Significant Digit): LSD와 반대의 방향으로 정렬을 진행
- 가장 큰 자릿수에서부터 정렬이 진행

정렬	특징
LSD	마지막에 가서 정렬순서를 판단(모든 데이터에 일괄적인 과정을 거친다.)
MSD	점진적으로 정렬을 완성(중간에 정렬이 완료될 수 있다.)

2-5. 기수 정렬의 구현: LSD 기준

🔻 구현

#include <stdio.h>
#include "ListBaseQueue.h"

#define BUCKET_NUM		10

void RadixSort(int arr[], int num, int maxLen)
{
	// 매개변수 maxLen에는 정렬대상 중 가장 긴 데이터의 길이 정보가 전달
	Queue buckets[BUCKET_NUM];
	int bi;
	int pos;
	int di;
	int divfac = 1;
	int radix;

	// 총 10개의 버킷 초기화
	for(bi=0; bi<BUCKET_NUM; bi++)
		QueueInit(&buckets[bi]);

	// 가장 긴 데이터의 길이만큼 반복
	for(pos=0; pos<maxLen; pos++)
	{ 
		// 정렬대상의 수만큼 반복
		for(di=0; di<num; di++)
		{
			// N번째 자리의 숫자 추출
			radix = (arr[di] / divfac) % 10;

			// 추출한 숫자를 근거로 버킷에 데이터 저장
			Enqueue(&buckets[radix], arr[di]);
		}

		// 버킷 수만큼 반복
		for(bi=0, di=0; bi<BUCKET_NUM; bi++)
		{
			// 버킷에 저장된 것 순서대로 꺼내서 다시 arr에 저장
			while(!QIsEmpty(&buckets[bi]))
				arr[di++] = Dequeue(&buckets[bi]);
		}

		// N번째 자리의 숫자 추출을 위한 피제수의 증가
		divfac *= 10;
	}	
}

버킷은 (연결 리스트 기반의) 큐를 기반으로 구현한다. (들어간 순서대로 꺼내기 위해)

🔻 성능평가

시간복잡도: $O(ln)\simeq O(n)$
- 데이터의 삽입과 추출이 핵심이다. (비교연산X)
- l: 모든 정렬대상의 길이, n: 정렬대상의 수

참고: 윤성우의 열혈 자료구조

deepTree

매일 노력하는 초보 개발자입니다.

이전 포스트

9. 우선순위 큐(Priority Queue)와 힙(Heap)

다음 포스트

10. 정렬(Sorting)

자료구조

1. 단순한 정렬 알고리즘

1-1. 버블 정렬의 이해와 구현

🔻 구현: 오름차순 기준

🔻 성능평가

1-2. 선택 정렬의 이해와 구현

🔻 구현: 오름차순 기준

🔻 성능평가

1-3. 삽입 정렬의 이해와 구현

🔻 구현

🔻 성능평가

2. 복잡하지만 효율적인 정렬 알고리즘

2-1. 힙 정렬의 이해와 구현

2-2. 병합 정렬의 이해와 구현

✔️ 기본 원리

🔻 구현

🔻 성능평가

2-3. 퀵 정렬의 이해와 구현

🔻 구현

🔻 성능평가

2-4. 기수 정렬의 이해

🚩 LSD 기수 정렬

2-5. 기수 정렬의 구현: LSD 기준

🔻 구현

🔻 성능평가

9. 우선순위 큐(Priority Queue)와 힙(Heap)

13. 테이블과 해쉬

0개의 댓글