VAE 추천 시스템 구현하기

학습 계기

최근에 소마에서 추천 시스템을 공부하면서 감정 기반 추천 시스템을 준비 할 일이 있었다.
하지만 감정 단어들은 word2vec 방식을 사용하였을 때 유사한 벡터값을 가진 것을 알 수 있다.
따라서 다른 감정 기반 추천 방식을 생각해 보았고,
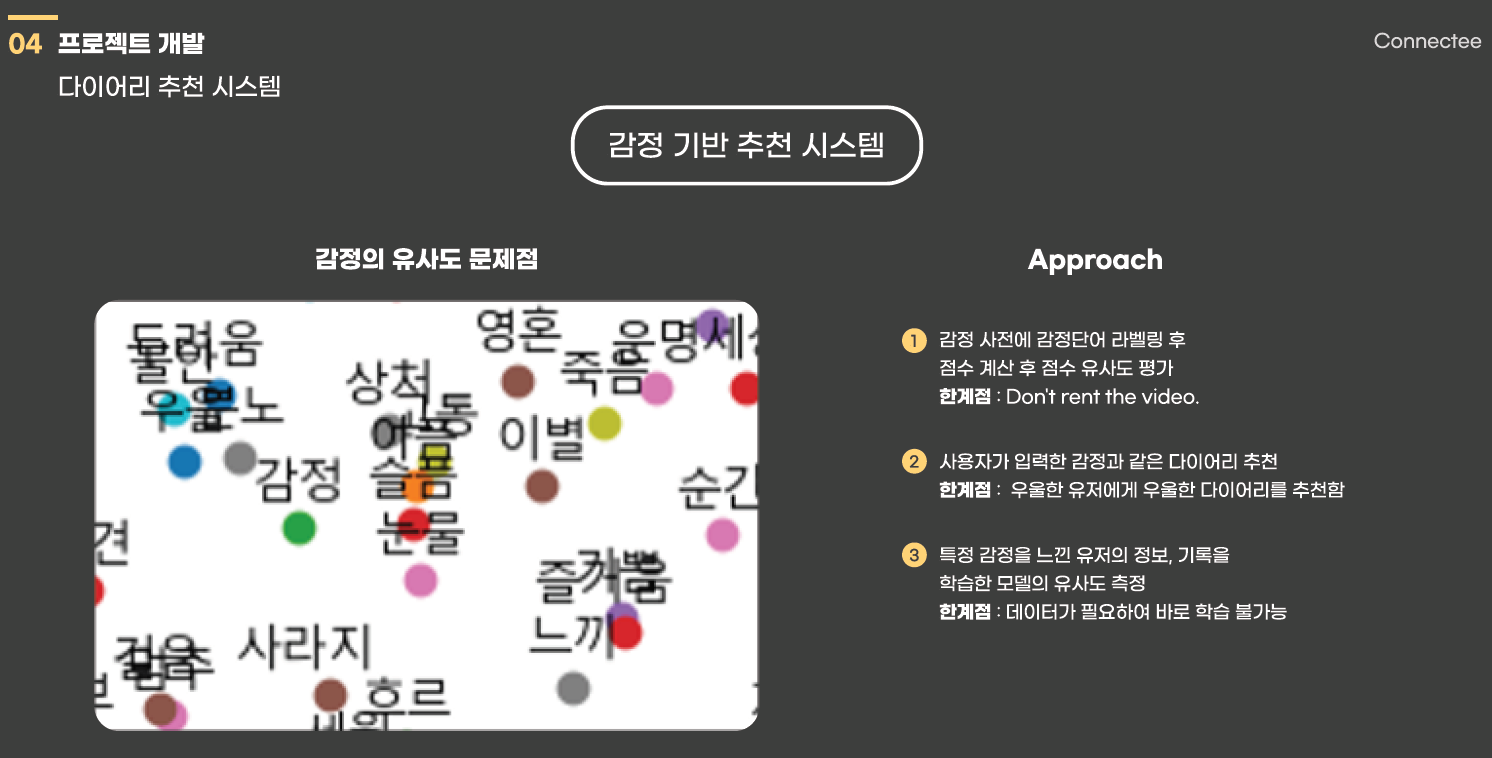
인터넷과 깃헙을 찾아보면서 감정 기반 분석 하는 경우가 3가지가 있었는데 위의 사진처럼
감정 단어 라벨링 이후 점수 계산을 통한 추천 하는 방식과 사용자가 입력한 다이어리 감정과 유사한 다이어리를 추천하는 방식을 생각하였으나 이 두가지는 보는 것과 같이 한계점이 분명하였다.

따라서 마지막에 작성한 것 처럼 특정 감정을 느낀 유저의 정보, 기록을 학습한 모델의 유사도를 측정하여 추천하는 방식을 생각하였다.
처음에는 Collaborative filtering 추천 방식인 Matrix Factorization을 생각하였으나 내적 등 선형 모델은 유저와 아이템 간의 복잡한 관계를 표현하는 데 한계가 있다는 것을 알게 되었다.
하지만 MF의 한계를 개선하기 위해 신경망 즉 활성함수를 추가한 방식인 auto Encoder을 공부하였고 (추가 하지 않은 AE도 존재한다.)
더 나아가 동작 원리는 다르지만 같은 인코더 디코더 형태를 가지고 있는 VAE(variational auto encoder) 를 사용하게 되었다.
물론 감정 기반 추천 시스템에서 VAE가 정답이라는 것이 아니다. 현재 트랜스포머를 활용한 bert도 존재하고 다양한 방법이 있을 것이다.

VAE를 이해하기 위한 사전 지식

AutoEncoder는 Manifold Learning 이다.

참고 : https://deepinsight.tistory.com/126?category=842339
우선적으로 AutoEncoder는 Manifold Learning 이다. AE는 인코더 부분을 학습하기 위해 뒷단을 붙여 학습을 진행 하고 입력 데이터를 압축하여 데이터의 의미있는 manifold를 학습한다.

여기서 manifold Learning 이란?
manifold 가설을 많이 들어 보았을 것이다. 아직까지도 증명이 안 된 부분이기도 하며
고차원 데이터를 학습하게 된다면 컴퓨터 부하나 리소스 낭비가 심하기 때문에 차원을 축소하는 방식이 필요하였다. 따라서 고차원 데이터가 차원에 존재 할 때 그 중 데이터를 잘 표현하는 작은 차원이 있을 것이라는 가정이다.
따라서 AE는 고차원의 데이터에서 그 데이터를 잘 표현 할 수 있는 latent variable를 뽑는 것으로 이해 할 수 있다.
이런 차원 축소 방법에는 linear 한 방식으로 유명 한 것이 PCA(principal Component Analysis) 방식과 non-linear 한 방식인 AE가 있다.

이 외에도 AE는 아래와 같은 특성을 가진다.

Unsupervised Learning -> 오직 input Data 만을 사용하기 때문이다.
Maximum Likelihood Density Estimation -> 앞에서 말한 학습 방법이 MLE와 동일하다

그래서 AE가 뭔데?

기존에 MF의 문제점을 해결하기 위해 비선형 활성 함수를 통해 성능 개선을 하였고
INPUT값으로 평점 추천, 순위 추천, 클릭 , 시청 여부로 자유롭게 활용 할 수 있으며 manifold learning을 통한 특정 latent variable을 뽑아 낼수 있는 모델을 말한다.

VAE를 이해해보자

VAE는 Generative Model 이다.

정의를 살펴보면 Generative Model은 train 데이터가 주어졌을 때 train data가 가지는 분포와 같은 분포에서 이상적인 sampling 된 값으로 new data를 생성하는 것을 말한다.

-> 말이 어려운데 이를 이해 하기 위해서는 추후 필자가 이해한 방식으로 풀어보고자 하며
우선은 VAE의 목적은 Generative model으로 어떤 새로운 x를 만들어 내는 것이다.

bayesian Theroy 의 정의에서 나아가 ML, MAP 까지

참고 : https://ddiri01.tistory.com/234#comment12176649%20%EC%B6%9C%EC%B2%98:%20https://deepinsight.tistory.com/127?category=842339%20[Steve-Lee's%20Deep%20Insight]

VAE를 이해하기 위해서는 베이시안 이론을 이해 해야 하며 베이시안 이론을 이해하기 위해서는 ML, MAP를 이해 해야 한다. 차근히 살펴보자.

우선적으로 동전을 던졌을 때 앞면이 나올 확률과 뒷면이 나올 확률은 같고 둘다 50%라는 것을 알 수 있다. 이는 천 번 , 수 만 번을 던져보았을 때 50%에 근사한 값을 가질거라는 즉 경험에서나오는
경험 확률 이다.
반대로 bayesian Theroy 는 일어나지 않은 일에 대한 확률을 불확실성에 근거하여 설명한다.
예를 들어 인천에 사는 허준현이 노벨상을 탈 확률은 몇인가에 대해 확률을 구하고 싶어도 인천에 사는 허준현의 case를 못 구할 때 사용하는 방식이다.

이런 베이시안의 확률은 사전 확률 P(A) 와 우도확률 P(B|A) 를 안다면 사후 확률 P(A|B) 를 구할 수 있다.

간단 설명( A: 모델 , B: 관측)

• P(B|A) 우도확률(Likelihood) : 어떤 모델에서 관측값이 나올 확률 (B의 확률)
• P(A) 사전 확률(Prior Probability) : 말 그대로 관측이 되기 전에 모델에 대해 가지고 있는 기존의 확률을 말한다.
• P(B) 확률 분포(evidence) : B에 대한 확률
• P(A|B) 사후확률(posterior probability) : 관측되고 난 이후 특정 모델에서 발생할 확률

다시 설명에 들어가기에 앞서 사전 확률 Prior 를 가정하기 어렵거나 측정할 수 없는 경우가 많을 것이다. 이 때 사용하는 것이 ML(Maximum-Likelihood) 를 사용하여 구한다. 이는 간접적인 확률인 P(B|A) 우도확률을 통해서 유추하는 방법과 P(A) 를 가정하여 최대의 posterior 값을 구하는 방법을 MAP(Maximum-A-Posterior) 라고 한다.
더 자세한 MAP, ML 설명은 블로그 참조 : https://jjangjjong.tistory.com/41

다시 한 번 MLE, MAP를 통해 베이시안 이론을 정리해 볼까?

https://hyeongminlee.github.io/post/bnn003_vi/
MLE는 lieklyhood만 주어진 경우 이를 최대로 하는 파라미터 w를 찾는 일,
MAP는 likelihood와 사전 확률인 prior가 전부인 경우 posterior를 최대로 하는 파라미터 w를 찾는 일이다!
베이시안 분포는 이런 파라미터 w의 확률분포, 즉 posterior를 말한다.
여기서의 베이시안 분포와 MAP의 차이는 MAP는 posterior의 최대로 하는 w의 값을 구하는 것이지 베이시안은 w의 확률분포를 구하는 것이므로 차이가 분명히 존재한다.
이제 posterior 를 구하기 위해 Bayesian Equation 식을 파해쳐 보자

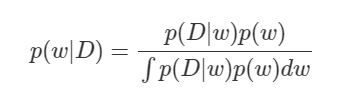
Posterior p(w|D) 는 train data D가 주어졌을 때 가장 재현 잘하는 w가 있을 것이고 이를 확정 짓지 않고 확률분포라고 하였다. 확정을 짓기 위해 식을 파해져 보면 p(D|w)는 우리가 앞서 살펴본 우도확률이며 정규 분포로 가정한다. 마지막으로 p(w) 즉 사전 확률인데 이는 우리가 원하는 분포로 설정하여 w를 구할 수 있게 된다.
언듯 보면 p(w|D)값을 구할 수 있을 것같지만 분모가 문제다. 분모에 있는 적분은 말 그대로 확률 분포를 나타낸다. 미분하는 값이 w 즉 파라미터로 미분을 하게 되는데 딥러닝의 layer가 깊어질수록 그 갯수는 많아지며 모든 w에 대해 적분을 하는 것은 사실상 불가능하다.

Posterior는 못구하는 것일까?

직접적으로는 찾기가 어렵다. 대신에 Variational Inference 를 통해서 간접적으로 구할 수 있다. Variational Inference는 우리가 모르는 함수가 있을때 비교적 적은 파라미터를 가지고 우리가 아는 함수 g를 정의하여 모르는 함수를 흉내내도록 파라미터를 정해 주는 것이다.

이 때의 파라미터를 θ 라고 정의하면 q(w|θ) 가 p(w|D)를 가장 잘 흉내내도록 q(w|θ)
의 parameter θ를 정해주는 것이다. 이 때 두 확률분포의 차이를 KL-Divergence로 나타내는데 뒤에 학습과정에서 Regularlizaion tern 에 해당하는 부분이며 아래에서 설명한다.

다시 한 번 위에서 VAE의 역할에 대해서 정의 해보자

train 데이터가 주어졌을 때 train data가 가지는 분포와 같은 분포에서 이상적인 sampling 된 값으로 new data를 생성하는 것을 말한다.

즉 train data가 속하는 P(A) prior Probability에서 여러가지 sampling 함수를 통해서 sampling을 진행하고 그 중 이상적인 feature를 뽑아내는 sampling을 선정하고 그 함수에 대해 x를 주어 학습을 한다.

이 부분에서 앞에서 언급한 sampling 함수 중에서 Posterior 에 제일 근사한 sampling 함수를 구하는 과정 즉, Variational Inference 에 해당하는 작업이다.

아마 위에서 MLE에 대해 공부하신 분이라면 이상적인 데이터가 있는 분포를 얻기 위해서 MLE를 바로 사용해도 되지 않는가에 대해서는 이활석님의 오토인코더의 모든것 강의를 추천한다.

결론적으로는 바로 MLE를 사용하게 된다면 MSE가 더 작은 데이터가 의미론적으로 더 가까운 경우가 아닌 이미지들이 많기 때문에 prior에서 샘플링을 하지 않는다.
아래의 PPT에서 a,b,c 중에서 c는 a를 오른쪽으로 픽셀을 미룬것인데 MSE 값이 c보다 b의 값이 높은 것처럼 예외 경우가 많다. 따라서 바로 MLE를 사용하는 것이 아닌 variational inference를 사용한다.

정리 : https://deepinsight.tistory.com/127?category=842339

VAE 이해하기

How can we perform efficient inference and learning in directed probabilistic models, in the presence of continuous latent variables with intractable posterior distributions, and large datasets?

파파고의 힘을 빌리면 난제의 사후 분포와 대규모 데이터 세트가 있는 연속 잠재 변수가 있는 경우 지시된 확률론적 모델에서 어떻게 효율적인 추론과 학습을 수행할 수 있는가? 이다.

이는 앞에서 말 했던 것처럼 정답은 train data와 같은 분포를 가지는 여러 sampling 함수들 중에서 이상적인 sampling 함수를 뽑고 train data값을 학습하여 새로운 데이터 x를 만든다.

VAE 구조 이해하기

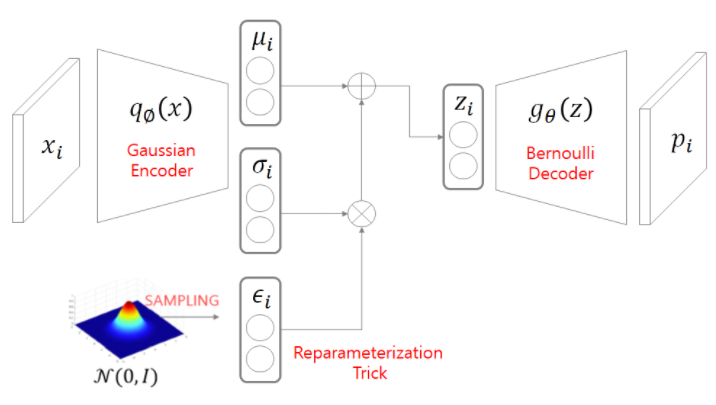
간략하게 인코더 부분에서 결과값의 𝜇,𝜎을 통해 latent-space(z) 를 만들고
z를 통해 복원하는 과정 까지 총 3단계 이다.

1. input: x –> 𝑞∅ (𝑥)–> 𝜇𝑖,𝜎_𝑖

2. 𝜇𝑖, 𝜎𝑖, 𝜖𝑖 –> 𝑧𝑖

3. 𝑧𝑖 –> 𝑔𝜃 (𝑧𝑖) –> 𝑝𝑖 : output

1. input: x –> 𝑞∅ (𝑥)–> 𝜇𝑖,𝜎_𝑖

인코더 부분에서 variational inference 방법으로 확률 분포 중에 x의 분포를 잘 나타내는 분포를 찾는 방안이다.
이때 확률 분포를 가우시안 분포(정규 분포) 라고 하면 𝜇𝑖,𝜎𝑖 를 추정하여 latent variable값을 찾는다.

따라서 Encoder 함수의 Output은 latent variable의 분포의 𝜇,𝜎 를 통해서 확률밀도함수를 생각할 수 있는 것이다.

2. 𝜇𝑖, 𝜎𝑖, 𝜖𝑖 –> 𝑧𝑖

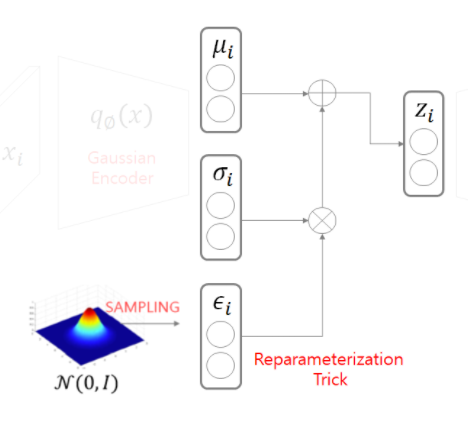
위의 사진을 보면 𝜇,𝜎 를 제외하고 추가적인 분포가 있는 것을 확인 할 수 있다. 이는 당연히 Encoder 결과에서 나온 값을 활용해 decode 하는데 추가적인 분포가 없다면 하나의 결과값만을 가지게 되는 동시에 역전파를 할 시에 𝜇,𝜎 까지 기울기값이 전달 받지 못하게 된다. 이는 앞에서 말했던 prior 와 같은 분포를 가지는 여러 sampling 함수 중에서 이상적인 sampling 함수를 뽑아내는 즉 variational inference 도입하였다.
이때 여러 sampling 함수가 위의 reparameterization Trick 부분에 추가해주는 것이다.

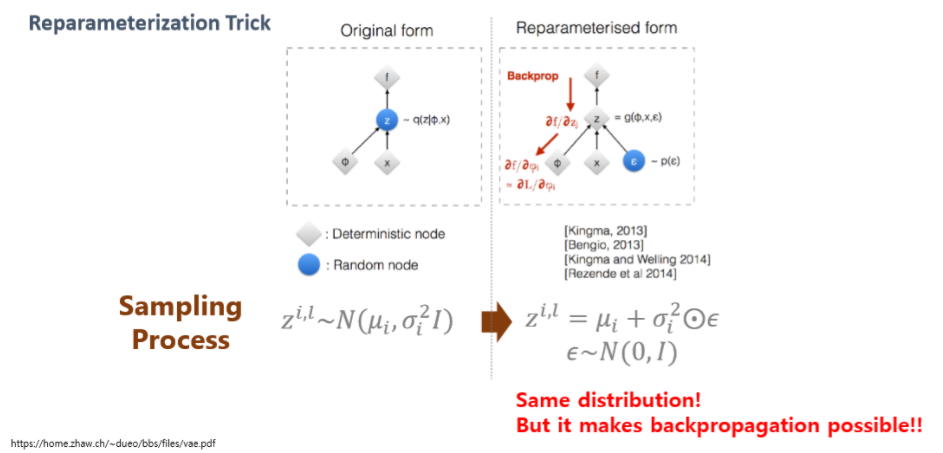
variational inference 을 하면서 얻게 되는 이점

1. 역전파를 통한 𝜇𝑖, 𝜎𝑖 업데이트
2. 간접적인 방식으로 Posterior 를 구해 p(w|D)에 근사한 확률 분포 획득
3. prior 와 동일한 확률 분포를 사용하여 즉 condition을 주어 z값을 다루기 용이해짐

1,2 코드 구현

1번 부분에서의 pytorch 의 encode 부분에서 𝜇,𝜎 값을 뽑아내는 것을 알 수 있으며 신경망을 사용자가 원하는 만큼 쌓으면 된다.
2번 부분에서 reparameterization Trick은 reparametrize에서 확인 할 수 있다.

# AutoEncoder 모델 설계
class Encoder(nn.Module):
    def __init__(self):
        super(Encoder,self).__init__()
        self.fc1_1 = nn.Linear(input, latent)
        self.fc1_2 = nn.Linear(input, latent)
        self.relu = nn.ReLU()
                        
    def encode(self, x):
        mu = self.relu(self.fc1_1(x))
        log_var = self.relu(self.fc1_2(x))
                
        return mu,log_var
    
    def reparametrize(self, mu, log_var):
        std = torch.exp(0.5*logvar)
        eps = torch.randn_like(std)
        return eps.mul(std).add_(mu)
    
    def forward(self,x):
        mu, log_var = self.encode(x)
        reparam = self.reparametrize(mu,log_var)
        
        return mu,log_var,reparam
        
encoder = Encoder().to(DEVICE)

3. 𝑧𝑖 –> 𝑔𝜃 (𝑧𝑖) –> 𝑝𝑖 : output

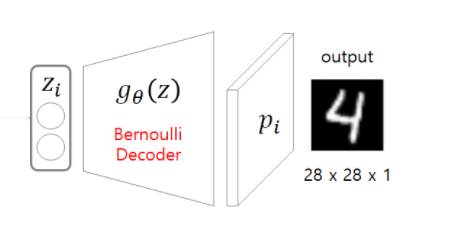
z값을 디코에 넣고 원래 train data의 사이즈로 돌리는 작업을 하는 것이다.
디코더 부분의 pytorch 코드는 다음과 같다. 이 때의 output 값을 0~1에서 설정하기 위해서 sigmoid를 사용하였고 각 상황에 맞는 활성에 맞는 손실함수를 밑에서 다룰 손실함수에서 적용해 주면 된다.

class Decoder(nn.Module):
    def __init__(self):
        super(Decoder,self).__init__()
        self.fc1 = nn.Linear(input, latent)
        self.simoid = nn.Sigmoid()
    
    def forward(self,x):
        out = self.fc1(x)
        out = self.simoid(out)
        
        return out

VAE 학습과정을 통한 최적화

참고 : https://deepinsight.tistory.com/127?category=842339
앞에서 말한 것처럼 prior 에서의 확률 분포와 동일한 확률분포를 가지는 sampling 함수를 통해 유사한 확률 분포 z를 만들기 위한 이상적인 sampling 함수를 찾는 것이다.
따라서 우리가 해야 하는 일은 prior 즉 p(X)값을 최적화 하는 것이며 log(p(x))값은 을 최대화 하는 것이 목표이며 log(p(x)) 의 최종식을 살펴보자.

위의 구현부분은 아래와 같으며 reconstruction 부분은 MSE로 , Regularlization 부분은 KLD_element 부분이며 앞에서 계속 언급한 sampling 함수와 prior의 차이를 말한다.
필자는 프로젝트와 어울리는 MSE 를 사용하였다.

reconstruction_function = nn.MSELoss(size_average=False)

def loss_function(recon_x, x, mu, log_var):
    MSE = reconstruction_function(recon_x, x)

    # see Appendix B from VAE paper:
    # Kingma and Welling. Auto-Encoding Variational Bayes. ICLR, 2014
    # https://arxiv.org/abs/1312.6114
    # 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
    KLD_element = mu.pow(2).add_(log_var.exp()).mul_(-1).add_(1).add_(log_var)
    KLD = torch.sum(KLD_element).mul_(-0.5)

    return MSE + KLD

parameters = list(encoder.parameters())+ list(decoder.parameters())
optimizer = torch.optim.Adam(parameters, lr=0.0005)

마지막으로 VAE 정리

VAE는 generative Model 즉 새로운 데이터 x를 생성하는 모델이다.

이 때 최대한 새로운 데이터 x를 train data 와 유사하게 만들려고 하며 이 때 MLE를 바로 사용하는 것이 아닌 prior와 동일한 확률 분포를 가지는 여러가지 sampling 함수들 중에서 이상적인 sampling 함수를 qΦ(z|x)를 사용하여 얻는다. 이 때 분포를 가정하기에 우리가 sampling에 대해 control을 할 수 있다는 점에서 특징들의 분포가 크게 벗어나지 않는 다는 것이다.
이 때 샘플링 함수를 통해 생성된 값이 train data와 최대한 같게 하기 위해 EqΦ(z|x)[log(p(x|g𝜃(z))] 값을 최대화 하는 MLE 문제를 푸는 과정을 통해 train data 와 유사한 x를 생성하는 것이다.

최종적으로 AE 와 VAE 비교

앞에서 설명 할 때 성능이 좋다고만 설명하였다. 하지만 그것 말고도 AE는 prior에 대한 조건이 없기 때문에 데이터를 생성할 때마다 z값이 계속 변경되는 것이다.
반면에 VAE는 prior에 대해 조건을 줄 수 있기 때문에 동일한 분포를 지니게 되면서 latent space가 다루기 용이해 진다. 따라서 여기서 Sparse한 부분이 줄어들고 더 유용한 Space를 얻기 때문에 성능차이가 나는 것이다.

추가적으로..

이 외에도 AutoEncoder에 대한 모든 것의 강의 마지막에 Conditional VAE, Adversarial AutoEncoder가 있으며 관심있는 사람은 추가적인 학습을 추천한다. 😀