Chi-Square Distribution (카이제곱 분포)

Theory

• The chi-square ($\chi^2$) distribution is a one-parameter family of curves. The chi-square distribution is commonly used in hypothesis testing, particularly the chi-square test for goodness of fit.
• $\chi^2(n)$ : chi-square
• Let $v=Z_1^2 + Z_2^2+...+Z_n^2;$ $Z=$i.i.d.$N(0,1)$
  Then, (by definition) $V ≈ \chi^2(n)$

Practice (MATLAB)

Ref) MATLAB 카이제곱 분포

Compute Chi-Square Distribution PDF

Compute the pdf of a chi-square distribution with 4 d.f.

x = 0:0.2:15;
y = chi2pdf(x,4);

figure;
plot(x,y)
xlabel('Observation')
ylabel('Probability Density')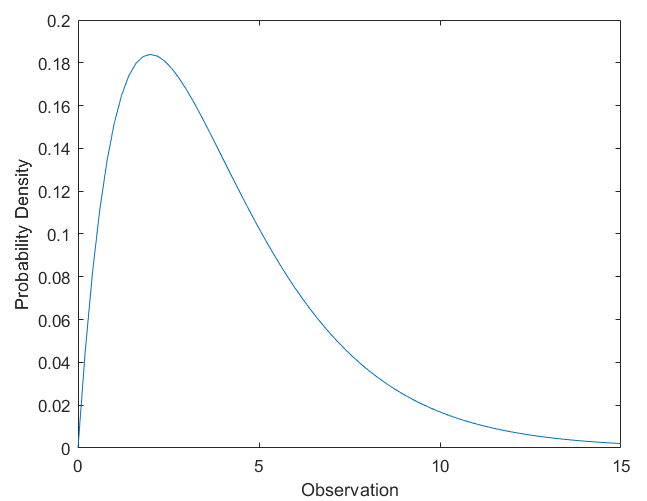

Compute Chi-Square Distribution CDF

Compute the cdf of a chi-square distribution with 4 d.f.

x = 0:0.2:15;
y = chi2cdf(x,4);

figure;
plot(x,y)
xlabel('Observation')
ylabel('Probability Density')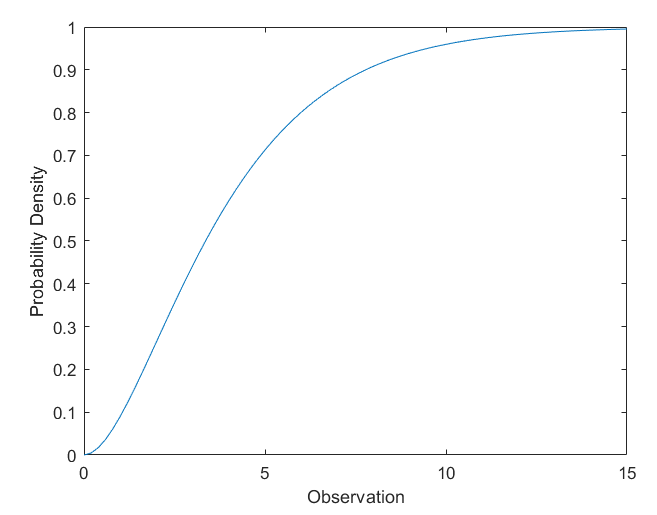

---

카이제곱 검정

Theory

Ref) 카이제곱 검정

1. 카이제곱 검정이란?

언제 카이제곱 검정을 할까?

• 변수가 명목척도인 경우.
• 자료(데이터) 의 값이 개수 (count)인 경우.

카이제곱 검정의 목적

• 변수가 한 개인 경우: 변수 내 그룹간의 비율이 같은지 / 다른지 확인
  • 단, 그룹이 2개인 경우 binomial test
  • 그룹이 여러 개인 경우 카이제곱 검정
• 변수가 두 개인 경우: 변수 사이의 연관성이 있는지 / 없는지
  • EX) 휴대폰 사용과 뇌암, 인종과 특정 질병

카이제곱 값

• O (observed frequency): 자료(데이터)에서 자연적으로 주어지는 값.
• E (Expected frequency): 개념적으로 이래야 한다는 기대 수치와 유사한 개념.

2. 일원 카이제곱 검정

• One-way ANOVA와 마찬가지로 일원(One-way) 란 변수가 1개라는 의미

Ex) 고객의 지불방법에 차이가 나는지 검정

Level	관찰빈도 (O)	기대빈도 (E)
Bank transfer	1544	1761
Credit card	1522	1761
Electronic check	2365	1761
Mailed check	1612	1761
total	7043

• $df = 4 - 1 = 3$
• ${\chi ^2}_{df = 3} = 278.95$
• $p - value < 0.001\,\,\, \to \,very\,significnat$

• 결론적으로 일원 카이제곱 검정의 유의성이 의미하는 것은 "무엇인가 다르다" 정도임.
• 여기서 다르다는 것은 사전에 정해진 기대빈도와 다르다는 의미임.
• 그래서 카이제곱 검정을 적합도 (goodness of fit) 이라고 부르기도 함.

3. 이원 카이제곱 검정

• 두 개의 명목척도를 가질 때
• 이 때 사용하는 것이 분할표(contigency table) 임.
  • 분할표: 두 개의 변수를 행(Row)과 열(column)로 나누어 빈도를 정리
• 분할표를 통해 카이제곱 검정을 하는 목적은 행과 열 사이에 (즉, 두 변수 사이에) 어떤 연관성이 있는지 확인해보는 것임.
  • 카이제곱 검정은 '연관성' 만을 확인하는 검사로 '인과성' 을 말해주는 것은 아님.

Ex1) Brain cancer와 cell phone 이 관련이 있을까?

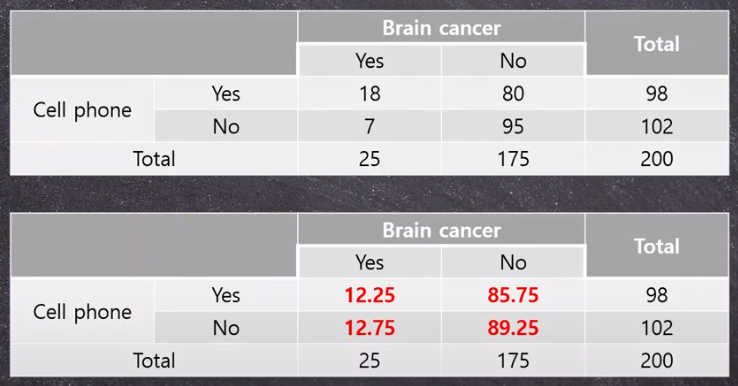
• 통계적 가설
  • H~0~: brain cancer와 cell phone 사용 간에는 연관성이 없다. (상호 독립적임)
  • H~1~: brain cancer와 cell phone 사용 간에 연관성이 있다.
• 기대빈도 계산법
  $E = {{(Row\,total) \times (Column\,total)} \over {Grand\,total}}$
  • ${\chi ^2} = 6.048$
  • $df = (2 - 1)(2 - 1) = 1$
  • $p - value = 0.014 \to significnat$

• 결론
  • Brain cancer와 cell phone 사용 간에는 연관성이 있다!

Ex2) 지진 보험은 지역에 따라서 편차가 큰가?

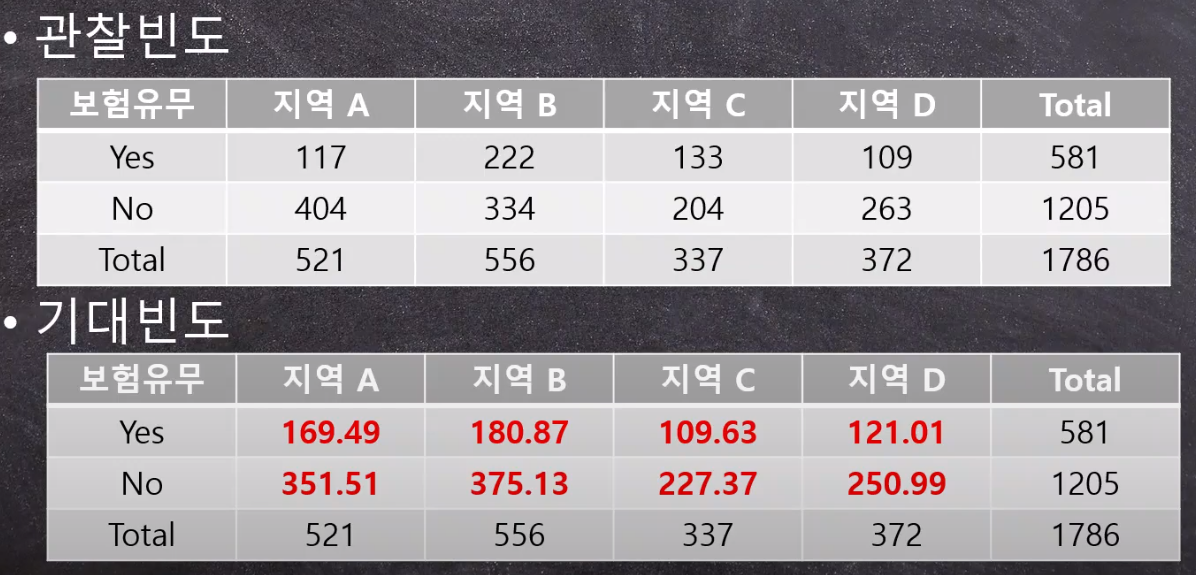
• 통계적 가설
  • H0: P(Yes|A) = P(Yes|B) = P(Yes|C) = P(Yes|D)
    P(No|A) = P(No|B) = P(No|C) = P(No|D)
  • H1: 지진 보험 가입 유무는 거주 지역과 연관성이 있을 것이다.
    (지진 보험을 가입했을 확률은 지역별로 다를 것이다.)

• ${\chi ^2} = 47.105$
  $df = (4 - 1)(2 - 1) = 3$
  $p - value < 0.05$

• 결론
  • 지진 보험 유무와 거주 지역은 통계적 연관성이 있음
  • 그러나, 문제는 범주 간의 확률의 차이가 얼마나 큰 지 알 수 없음.
  • 이러한 문제를 해결하기 위해서는 CI (Confidnece Interval) 신뢰구간을 이용

4. 카이제곱 검정을 넘어

한계점 or 전제조건

• 랜덤 샘플링을 전제로 함.
• 독립성
  • 각 범주가 서로 배타적이어야 함.
  • 한 대상이 하나 이상의 범주에 들어갈 수 없음.
• 각 셀의 기대빈도가 5 이상이어야 함.
  • 기대빈도를 5 이상으로 맞추기 위해 경우에 따라 범주를 합쳐야 함.
  • 만약 범주를 합칠 수 없다면, Fisher's exact test (피셔의 정확검정)을 하거나, likelihood ration test (G-test)를 해야 함.
• 만약 df가 1이라면
  • 문제는 비연속성의 조건부 확률을 연속성의 카이제곱 분포에 적용함으로써 발생
  • 일원 카이제곱 검정의 경우 무조건 연속성 보정을 하는 Yate's correction 또는 카이제곱 continuity correction 을 사용해야 함.
  • 다만, 이원 카이제곱 검정의 2x2인 경우, 카이제곱 test 결과와 Yate's correction 결과가 다를 때에는 Fisher's exact test 사용

그 외 것들

• 두 명목척도인 변수가 연관성이 있을 경우
  • 얼마나 상관관계가 높은지 궁금할 때, 상관계수를 구하는 방법
    • Contigency coefficent (분할계수/C계수)
    • Phi and Cremer's V (좀 더 안정적임)
• 만약 변수가 순위척도이고 연관성이 있다면
  • 얼마나 상관관계가 높은지 알고 싶다면
    • Kendall's tau-b
    • Gamma

Practice (MATLAB)

Ref) MATLAB 카이제곱 적합도 검정

Chi2gof

'카이제곱 적합도 검사'를 통해 '벡터 x의 데이터가 평균과 분산이 x에서 추정된 정규분포에서 추출된다'는 귀무가설에 대한 검정 결과를 반환함.

정규분포 여부 검정하기

표준 정규 확률 분포 객체를 만듭니다. 이 분포에서 난수를 사용하여 데이터 벡터 x를 생성합니다.

pd = makedist('Normal')
rng default;  % for reproducibility
x = random(pd,100,1);

'x'의 데이터가 정규분포를 따르는 모집단에서 추출된다'는 귀무가설을 검정합니다.

h = chi2gof(x)

반환된 값 h=0 은 chi2gof가 디폴트 5% 유의수준에서 귀무가설을 기각하지 않음을 나타낸다.

Example

bins = 0:3;
expCounts = [1761 1761 1761 1761];
obsCounts = [1544 1522 2365 1612];

[h,p,st]= chi2gof(bins, 'Ctrs', bins, ...
                        'Frequency',obsCounts, ...
                        'Expected', expCounts, ...
                        'NParams', 0, ...
                        'Alpha', 0.05)