Theory

Ref) Harvard Statistics110 - The Poisson distribution

Poisson Distribution 이란?

• 표집된 단위 시간 (혹은 단위 공간)에서 발생한 사건의 도수 분포
• 단위 시간 안에 몇 번 발생할 것인지를 표현하는 이산 확률 분포
• 푸아송 분포의 기대값 및 분산은 $\lambda$

PMF of Poisson Distribution

• Is it valid PMF?

• Expectation value

When use?

• 주어진 시간,거리,면적 등에서 임의 사건이 발생하는 횟수를 세야 하는 경우에 적합.
  • Ex) 초당 클릭 횟수, 시간당 매장에 들어오는 사람 수, 1분에 네트워크에서 손실되는 패킷 수 등
• 굉장히 여러 번 시행하지만 성공확률이 낮은 경우에 사용.
  1. Number of emails in hour.
  2. Number of chips in chocolate chip cookies.
  3. Number of earthquakes in a year in some region.

Poisson Paradigm (Poisson Approximation)

• Events $A_1$, $A_2$, ... $A_n$, $P(A_j)=p_j$ ($n$ is large, $p_j$ is small)
• 각각의 사건들이 "independent" or "weakly independent" 하다면,
  Then # of $A_j$'s that occur is approximated as $Pois(\lambda );\,\,\lambda = \sum\limits_{j = 1}^n {{p_j}}$

이항분포가 어떻게 푸아송 분포로 수렴하려는가?

$X \sim Bin(n,p)$, let $n\to\infty$, $\lambda=np$ is held constant.
Find what happens to
$\kern{3em}P(X=k)=(\substack{n\\k})p^k(1-p)^{n-k}$, $k$ is fixed.
$\kern{7.6em}= {{n(n - 1) \cdots (n - k + 1)} \over {k!}}{{{\lambda ^k}} \over {{n^k}}}{\left( {1 - {\lambda \over n}} \right)^n}{\left( {1 - {\lambda \over n}} \right)^{ - k}}$
$\kern{7.6em}= {{{\lambda ^k}} \over {k!}}{e^{ - \lambda }}$, Poisson PMF at $k$

---

Practice (MATLAB)

Ref) MATLAB Poisson distribution

푸아송 분포의 pdf 계산하기

모수 lambda=4 를 갖는 푸아송 분포의 pdf를 계산해보자.

x = 0:15;
y = poisspdf(x, 4);

figure();
bar(x,y,1)
xlabel('Observation')
ylabel('Probability')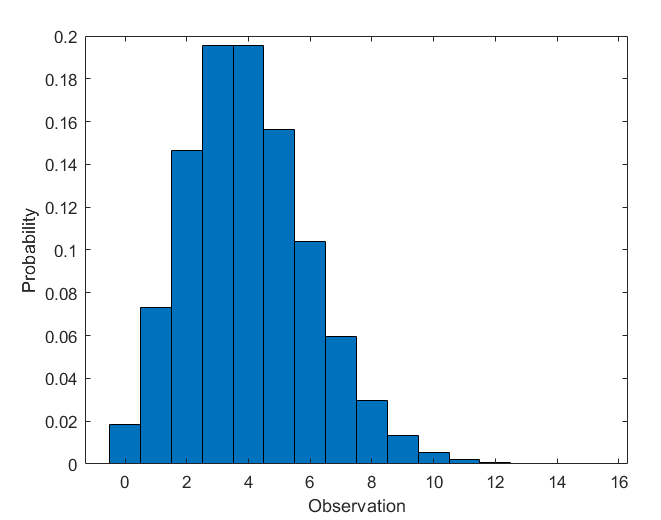

푸아송 분포의 cdf 계산하기

x = 0:15;
y = poisscdf(x,4);

figure;
stairs(x,y)
xlabel('Observation')
ylabel('Cumulative Probability')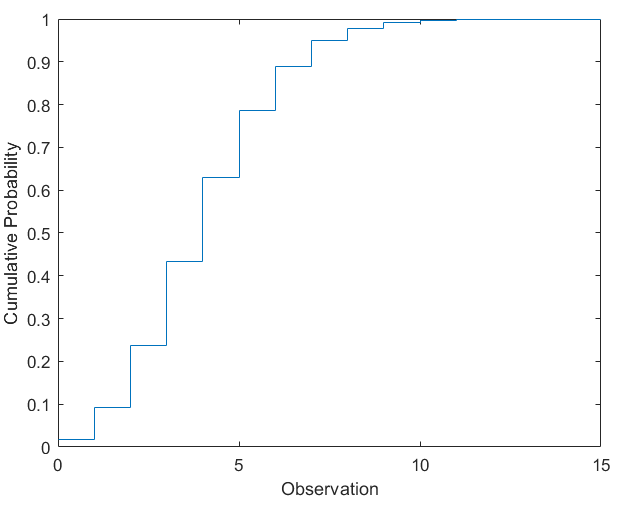

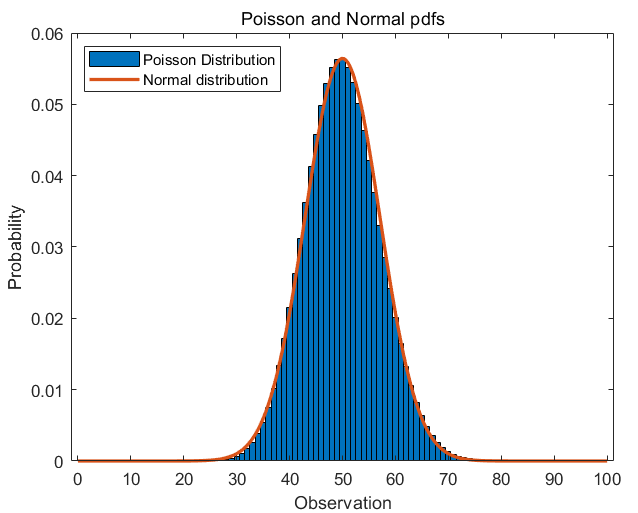
푸아송 분포 pdf와 정규분포 pdf 비교하기

labmda가 크면 푸아송 분포는 평균 lambda와 분산 lambda를 갖는 정규분포로 근사가 가능하다.
모수 labmda=50을 갖는 푸아송 분포의 pdf를 계산해보자.

lambda = 50;
x1 = 0:100;
y1 = poisspdf(x1, lambda);

mu = lambda;
sigma = sqrt(lambda);
x2 = 0:0.1:100;
y2 = normpdf(x2,mu,sigma);

figure;
bar(x1, y1, 1)
hold on
plot(x2, y2, 'LineWidth', 2)
xlabel('Observation')
ylabel('Probability')
title('Poisson and Normal pdfs')
legend('Poisson Distribution', 'Normal distribution', 'location', 'northwest')
hold off