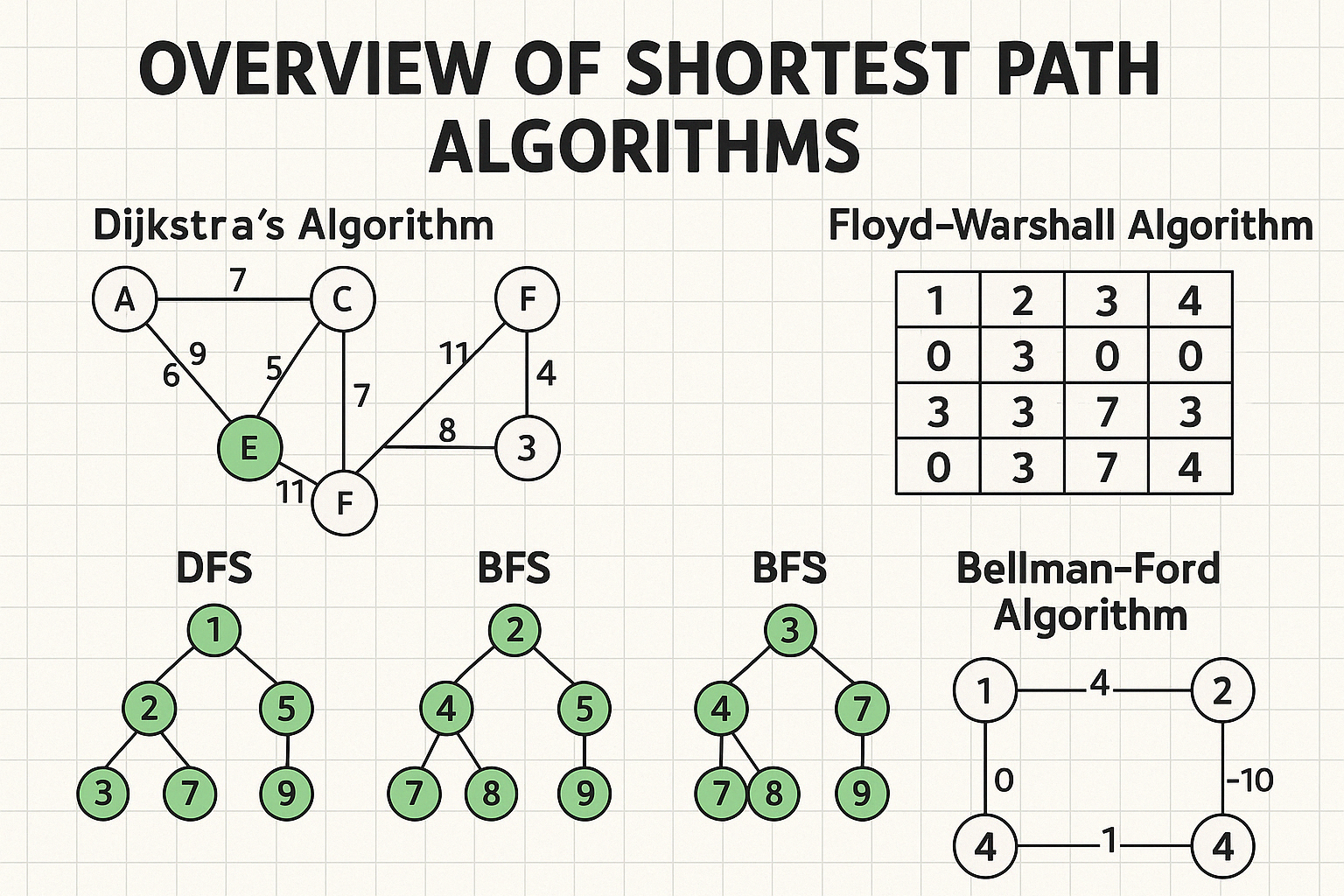
알고리즘 문제를 풀이하면서 가장 많이 만나는 문제 유형인 최단 거리 알고리즘에 대해 정리해보도록 하겠다.
보통 최단거리 알고리즘은 간선(edge)의 가중치 유무, 음수 가중치 존재 여부, 모든 정점 간 vs 단일 출발점 문제에 따라 선택이 달라진다.
먼저 결론부터 말하자면,

• 가중치가 없거나 모두 1이면 BFS
• 양수 가중치일 경우 다익스트라
• 음수 가중치를 포함할 경우 bellman ford
• 모든 정점간의 경로를 구하고자 한다면 플로이드 워셜
  알고리즘을 활용한다.

다익스트라 알고리즘 (Dijkstra)

두 노드를 잇는 가장 짧은 경로 즉 최단경로를 찾아야 할 때 주로 사용한다.
또한 가중치가 존재하는 그래프에서 주로 사용한다.

첫 노드를 기준으로 연결되어 있는 노드들을 추가하며 최단 거리를 갱신하는 알고리즘이다.
A에서 출발하여 F까지 가는 최단 거리를 찾는다.
라는 의미로 해석하면 이해하기 쉽다.

한줄요약 : 가중치가 양수일 때, 하나의 출발점에서 모든 정점까지의 최단거리를 구하는 알고리즘이다.
핵심 : Greedy방식으로 현재 가까운 노드를 우선적으로 방문하며 거리를 갱신한다. Priority Queue를 사용하면 효율적이다.
시간 복잡도 : O((N + E) log N)

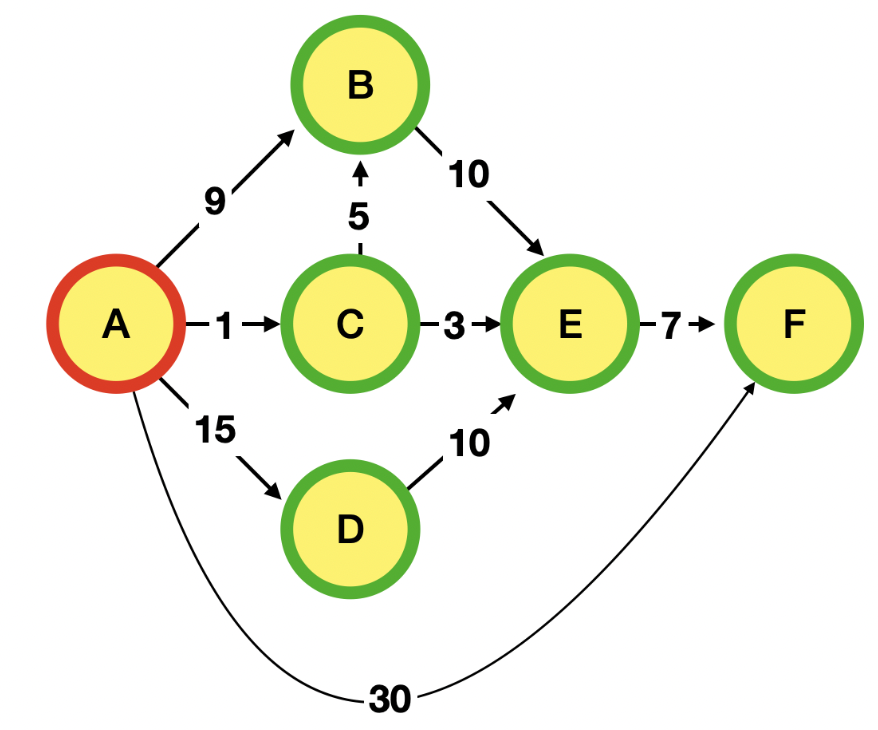
그래프를 보며 쉽게 이해해보도록 하자
각 상황에서 본인을 제외한 최단노드를 뽑아야 하기 때문에 우선순위 큐가 필요한것이다.
노드의 갯수만큼 배열을 생성, 출발노드의 값은 0, 나머지 값들은 INF(무한)으로 초기화한다.
우선순위 큐를 생성하고, 첫 노드의 가중치를 0으로 한다.

우선 순위 큐에서 값을 추출하고 인접한 노드들과 거리를 계산한다.
위 그림을 예로 든다면
A -> B : 9 + 0(A)
A -> C : 1 + 0(A)
A -> D : 15 + 0(A)
해당 값들이 INF로 저장된 값들보다 작기 때문에 update
그리고 방문한 노드들을 우선순위 큐에 저장한다.
해당 단계 후 변화된 배열
A B C D E F
0 9 1 15 INF INF
우선순위 큐(거리가 짧은 순으로)
C B D

---

이제 해당 단계를 우선순위 큐가 빌 때까지 진행한다
이해를 위해 몇단계만 더 진행해보도록 하겠다
C -> B : 5 + 1(C)
C -> E : 3 + 1(C)
변화된 배열
A B C D E F
0 6 1 15 4 INF
우선순위 큐
E B(6) B(9) D

---

E -> F : 7 + 4(E)
변화된 배열
A B C D E F
0 6 1 15 4 11
우선순위 큐
B(6) B(9) F D

---

그렇게 최종 결과는 다음과 같이 종료된다
A B C D E F
0 6 1 15 4 11

플로이드-워셜 알고리즘(Floyd-Warshall)

그래프에서 자주 출제되는 문제 유형이다.
크루스칼 알고리즘과 플루이드 와샬이 대표적인 그리디 알고리즘이다.
그 중 여기서는 플로이드 워셜 알고리즘에 대해 알아보자.

'모든 지점'에서 '모든 지점'까지의 최단 경로를 모두 구해야할 때 사용할 수 있는 알고리즘이다.

매번 방문하지 않은 노드중에서 최단 거리를 갖는 노드를 찾
을 필요가 없다는 점에서 다익스트라와 다른점이라고 할 수 있다.

한줄요약 : 모든 정점 간의 최단거리를 구하는 DP 기반 알고리즘
핵심 : 각 정점이 경유지가 될 수 있다는 점에 착안해 3중 루프로 모든 경로를 갱신
시간 복잡도 : O(N^3)
주의 : N이 500 이하일때만 가능

총 N번의 단계를 수행하며, 수행하는 단계마다 O(N^2)의 연산을 통해 계산한다
따라서 N * O(N^2) -> O(N^3)의 시간복잡도를 가진다.

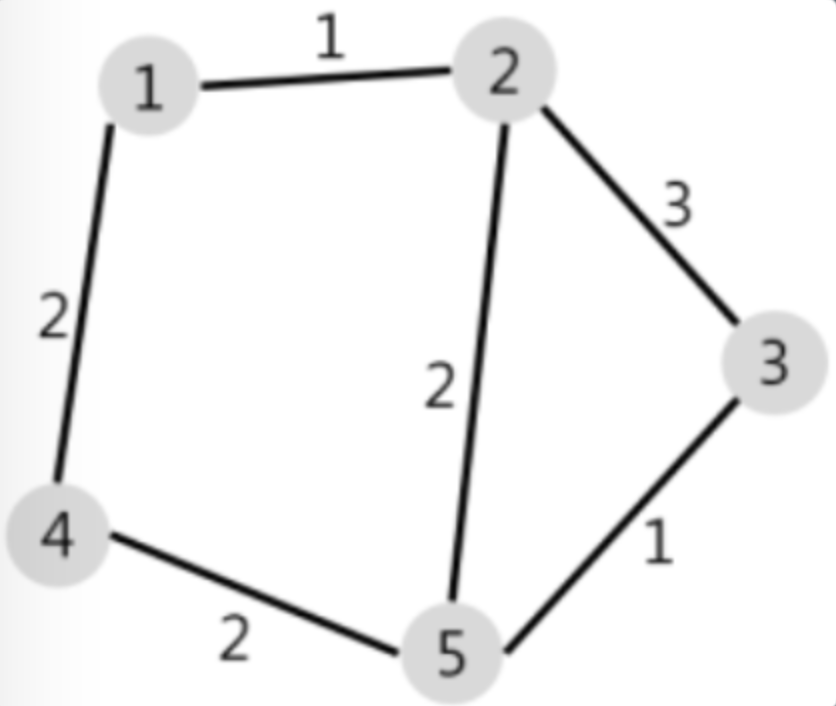
그래프를 보며 쉽게 이해해보도록 하자
위의 그림을 예로 들 때, 1에서 5까지 가는 최소 비용은
1 - 2 - 5 -> 비용 3이다.

func Floyd_Warshall() {
  for i in 0..<N {
    for j in 0..<N {
      for k in 0..<N {
        node[j][k] = min(node[j][i] + node[i][j], node[j][k])
      }
    }
  }
}

코드가 복잡하지 않아 이해하는데는 어려움이 없을것이다.
node[j][k]값과 node[j][i] + node[i][k]중 작은값을 결과값으로 지정한다.
즉, j에서 k까지 갈때, i라는 경유지를 거쳐서 가는 경우를 비교하는 것이다.

해당 경우를 이용해 알고리즘 문제를 풀이한 경우가 있다
2021 KAKAO BLIND RECURITMENT - 합승 택시 요금

이쯤에서 궁금한 점이 있다.
시간복잡도가 O(N^3)인 알고리즘을 왜 알아야할까?
다익스트라 알고리즘은 그래프에서 최단 거리를 찾는 가장 대표적인 알고리즘이다.
특정시작지점에서 모든 노드까지의 최소 거리를 알 수 있는데
그냥 N번 반복하여 각각의 노드를 전부 시작지점으로 설정해서 모든 노드로의 거리를 구하면 끝 아닌가?
복잡도 또한 다익스트라 O(VlogV + E)에 N번 반복 = O(N(VlogV + E))이 될텐데 말이다.
이유는 단순하다.
플로이드 워셜 알고리즘은 다익스트라와 달리 가중치가 '음수'여도 가능하기 때문이다.
하지만 3중 반복문의 크기는 상당히 크기 때문에 노드의 크기가 500 이상이라면 이용하기 쉽지 않다.

깊이 우선 탐색(DFS)

말 그대로 깊이 우선 탐색, 너비 우선 탐색이다.
DFS는 가중치와 무관하게 깊이 우선 탐색을 수행하며, 최단 거리 보장은 하지 않는다.

한줄 요약 : 한 방향으로 깊게 탐색하는 방식으로, 최단거리를 보장하지는 않지만 경로 탐색에 활용
핵심 : 스택 또는 재귀 호출을 통해 깊이 우선 탐색
시간복잡도 : O(V + E)

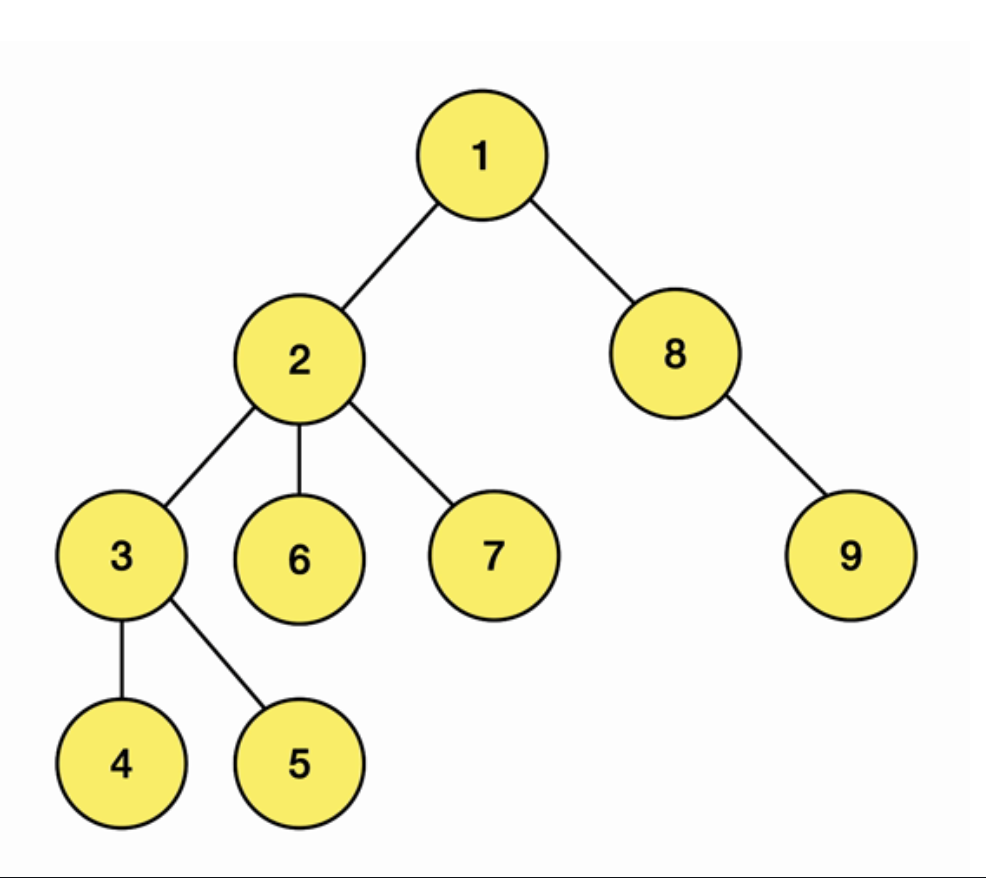
위 그림대로 탐색노드의 인접 노드의 자식 노드들을 모두 탐색하고, 다시 돌아가서 탐색노드의 다른 인접노드로 향하는 방식이다.
보통 큐하나와 스택 하나로 구성이 된다.
방문한 VisitedQueue as Q(FIFO)
방문해야 할 needVisitStack as S(LIFO)이다.
위 사진을 그래프로 표기하면 이와 같다.

1 - 2 8
2 - 3 6 7
8 - 9
3 - 4 5
6 - 2
7 - 2
9 - 8
4 - 3
5 - 4

스택의 마지막 값을 추출해서 visiedQueu에 해당 값이 있는지 확인한다.
만약 이미 방문했던 노드라면 추출값을 버리고 Stack에서 다음값을 뽑는다.
위 과정을 visiedQueue에 없는 값이 나올때 까지 반복하는데
이러다 stack이 비게 된다면 탐색이 끝나게 된다.

이해를 위해 몇번의 과정을 보여주도록 하겠다

이제 1부터 탐색을 시작한다고 하자
Q
S - 1
방문했던 노드가 아니기에 visitedQueue에 넣는다.
그리고 연결된 간선들을 stack에 넣는다.
Q - 1
S - 2 8
다시 위의 과정을 반복
8을 추출하던 2를 추출하던 사실 상관없다.
어떤 인접 노드부터 탐색할지는 순서가 없기 때문이다.
Q - 1 8
S - 2 9
8을 뽑고 방문한 사실이 없기에 8을 Q을 넣고 8의 자식노드를 stack에 넣는다.
Q - 1 8 9
S - 2 8
9를 뽑고 방문한 사실이 없기에 9를 Q에 넣고 9의 선택노드인 8을 넣는다.
Q - 1 8 9
S - 2 1

위의 과정을 반복한 결과
최종 : Q - 1 8 9 2 7 6 3 5 4 의 결과가 나온다
사실 최단 거리 계산보다는 경로 탐색에 유용하다.
dfs와 bfs의 차이를 위해 작성한다.

너비 우선 탐색(BFS)

말 그대로 너비 우선 탐색이다.

한줄 요약 : 모든 간선의 가중치가 동일(또는 1)일 때, 최단 경로를 구할 수 있는 탐색 알고리즘
핵심 : 가까운 정점부터 차례대로 방문하므로, 처음 도착한 경로가 곧 최단거리
시간복잡도 : O(V + E)

방식은 DFS과 똑같다고 할 수 있다.

Q - 1
S - 2 3
---
Q - 1 2
S - 3 4 5 6
---
Q - 1 2 3
S - 4 5 6 7

등등 이 반복되다
Q - 1 2 3 4 5 6 7 8 9가 되는 것이다.

중요한 점은 큐를 사용하고, 가까운 곳부터 탐색한다는 것이다.

벨만-포드 알고리즘(Bellman-Ford)

벨만포드 알고리즘은 다익스트라 알고리즘의 단점을 해결한 알고리즘이다.
다익스트라 알고리즘은 간선들의 거리가 음수라면 최소거리를 찾을 때도 있고 못찾을 때도 있다.
또한 벨만 포드 알고리즘은 Greedy 해결법이 아닌 dp를 사용한다.
물론 플로이드 워셜 알고리즘을 통해 음수의 거리들을 속에서 최단거리를 찾을 수도 있다.
하지만 플로이드 워셜 알고리즘은 O(n^3)이기에 노드의 크기가 500 이상이라면 시간초과가 나게된다.

한줄 요약 : 음수 가중치까지 포함된 최단거리를 구할 수 있는 알고리즘
핵심 : 모든 간선을 최대 V-1번 반복하며 Relaxation 수행, 음수 사이클까지 탐지할 수 있음
시간복잡도 : O(V × E)

해결법

최단거리를 dist[]배열에 저장할 때, 항상 dist[cur] + cost[next] < dist[next]이라면
최단거리는 dist[cur]이다.
dist[v] <= dist[cur] + w(current,v)이라는 것이다.
시작점 s-v까지 가는 최단거리는 s-next까지 가는 최단거리에 current-v까지의 가중치를 더한 값보다 클 수 없다.
n - 1 번 반복하여, 모든 간선에 대해 경로를 최소값으로 갱신이 가능한지 확인해준다면
음의 간선이 있어도 최단 경로를 구할 수 있다.

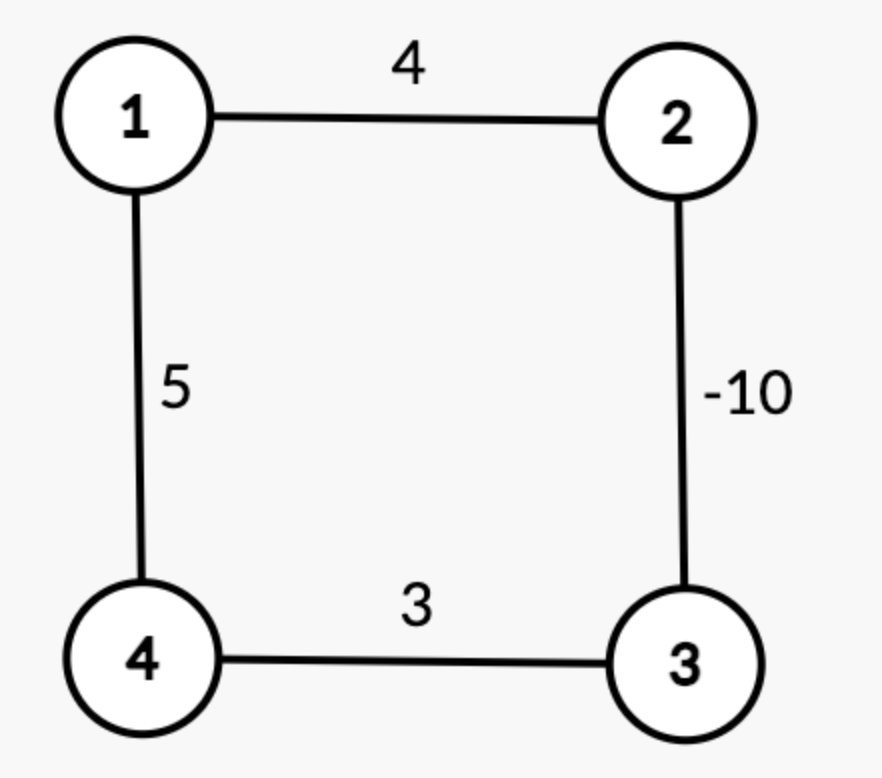
그림을 예시로 더 쉽게 이해해보자

우리는 V-1번 반복하게 된다.
즉, 3번의 간선정보를 통해 최단거리를 찾을 수 있다.
1에서부터 시작한다고 가정하고 시작값에는 최단거리 0, 그외의 값들에는 INF를 넣는다.

초기값
1 2 3 4
0 I I I

1번 실행
1 2 3 4
0 4 I 5

2번 실행
1 2 3 4
0 4 -6 5

3번 실행
1 2 3 4
0 4 -6 -3