딥러닝을 위한 선형대수학

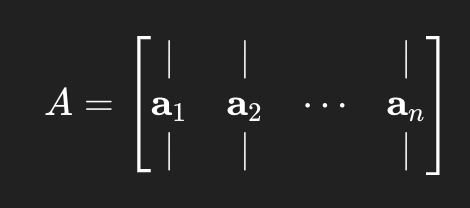
1\. 행렬 곱셈을 열의 조합으로 본 관점mxn 행렬 A = a1, a2, ..., an과 열벡터 $x=(x1, x2, ...xn)^T$가 있을 때, 곱 Ax는 다음과 같이 열 벡터들의 선형결합으로 해석할 수 있다.$$Ax = x_1a_1 + x_2a_2 + ... +

1\. 외적 (Outer Product)여러 개의 랭크 1 행렬의 합이란?행렬의 랭크는 그 행렬의 열(또는 행)들이 생성하는 공간의 차원이다.쉽게말해 선형독립인 열벡터(또는 행벡터의) 개수가 랭크이다. 행렬이 나타내는 선형 변환이 얼마나 많은 독립적인 방향을 갖고 있는

1\. 열공간 (Column Space), C(A)A의 열 벡터들이 생성하는 공간차원 : rank(A)2\. 행공간 (Row Space), C($A^T$)$A^T$가 생성하는 공간차원 : rank(A)(열공간과 동일)3\. 영공간 (Nullspace), N(A)Ax=0

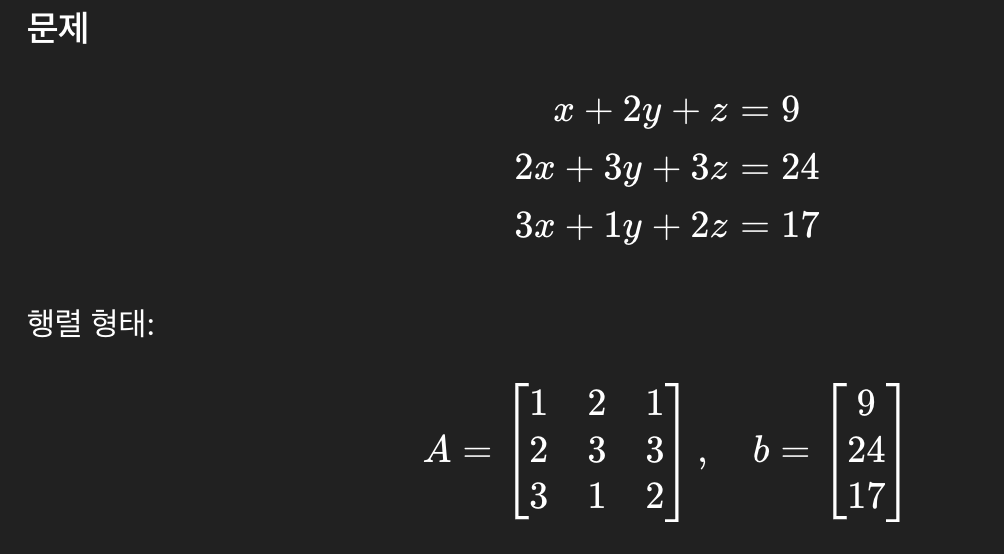
1\. Gaussian Elimination(가우시안 소거법)개요행렬 A에 일련의 행 연산을 수행하여 상삼각 행렬 U로 변환하는 과정이다.이 소거 과정은 행렬의 계수(rank), 열공간, 영공간 구조를 찾는 데 핵심적 방법이자 시각적 도구이다.목적 및 의미기저열을 찾아

1\. 직교행렬 개념직교행렬 Q는 다음 성질을 만족 $$Q^TQ = I (=Q^-1 = Q^T)$$즉, 행과 열이 서로 직교하고 단위 벡터인 행렬직교 기저 개념 확장행/열 벡터가 서로 직교하고 길이가 1인 기저2\. 직교행렬이 중요한 이유\* 수학적 관점에서 중요한 이

1\. 고윳값과 고유벡터의 정의행렬 A에 대해 Av = $\\lambda$v 를 만족하는 v가 0이 아닌 벡터를 고유벡터, 그에 대응하는 스칼라값을 고유값이라고 한다.기하학적으로는, 고유벡터는 선형 변환의 방향을 변경하지 않고 단지 길이만 $\\lambda$배로 늘리거