Manifold란 고차원 데이터가 있을 때 고차원 데이터를 데이터 공간에 뿌리면 sample들을 잘 아우르는 subspace가 있을 것이라는 가정에서 학습을 진행하는 방법이다.
이렇게 찾은 manifold는 데이터의 차원을 축소시킬 수 있다.

Manifold Learning은 언제 사용될까?

1. Data Compression
2. Data Visualization
3. Curse of dimensionality
4. Discovering most important features
   
   

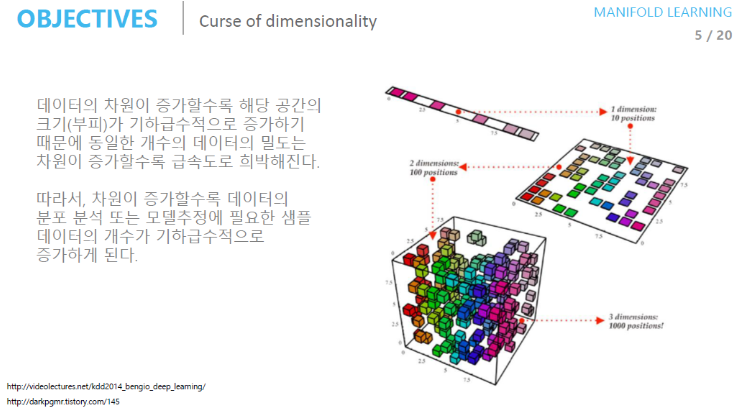
• 데이터의 차원이 증가할수록 해당 공간의 크기(부피)는 기하급수적으로 증가한다.
• 동일한 개수의 데이터의 밀도는 차원이 증가할수록 급속도로 희박해지게 된다.
• 따라서 차원이 증가할수록 데이터 분포 분석 또는 모델 추정에 필요한 샘플 데이터의 개수가 기하급수적으로 증가하게 된다.
  
  

Manifold의 가정

고차원의 데이터는 밀도가 낮지만 이를 포함하는 저차원의 manifold가 있다.
이 저차원의 manifold를 벗어나는 순간 밀도는 급격히 낮아지게 된다.
즉, 고차원의 데이터를 잘 표현하는 manifold를 통해 샘플 데이터의 특징을 파악할 수 있다.

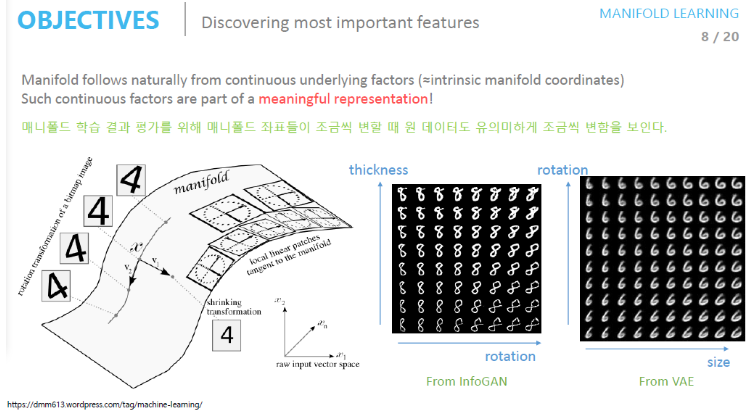
manifold는 고차원 데이터를 잘 표현한다고 배웠다.
(고차원의 데이터를 잘 표현한다 = 데이터의 중요한 특징을 발견한다)
고차원 데이터의 manifold 좌표들을 조정해보면 manifold의 변화에 따라 학습 데이터도 유의미하게 조금씩 변하는 것을 확인할 수 있다.

Data(샘플)를 잘 아우르는 manifold를 찾게 되면 어떤 효과가 있을까?

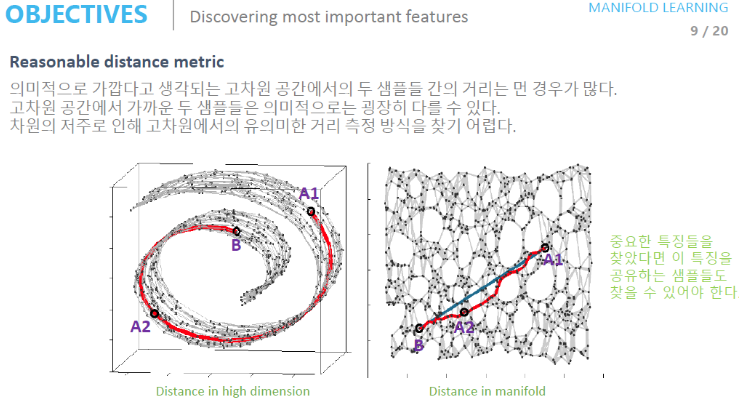
• feature를 잘 찾았기 때문에 manifold의 좌표를 조금씩 변경해가면서 데이터를 유의미하게 조금씩 변화시킬 수 있다.
• 이는 data의 dominant한 feature를 잘 찾았기 때문이다.
• 반대로 manifold를 잘 찾았다면 dominant feature가 유사한 sample들을 찾아볼 수 있다.

Dimensionality Reduction Taxonomy

: 차원 축소 분류

ML에 대해 공부를 했다며 PCA 알고리즘을 들어봤을 것이다. 간단하게 말하자면 원본 데이터를 공간에 뿌려 hyper plane을 찾는 방법이다. 이때 PCA 알고리즘의 수식은 우리가 Neural Network에서 사용하는 Linear한 수식이 된다. 이 때문에 Taxonomy(분류)에서는 Linear한 방법으로 분류된다.

다음 챕터부터 다룰 AutoEncoder는 Non-Linear한 방법이다.