Covariance and Correlation

Questions

• 두 변수가 서로 연관되어 있다는 것은 무슨 의미인가?
  • 예를 들어, "공부 시간"과 "시험 점수"가 있을 때, 공부 시간이 늘어날 때 시험 점수도 함께 높아진다면, 이 두 변수는 "연관되어 있다"고 말할 수 있다.
• 이러한 연관성을 수학적으로 어떻게 표현할 수 있는가?
  • 단순히 "관계가 있어 보인다"가 아니라, 숫자로 정확히 측정하는 방법이 필요하다.
  • 이것이 공분산(Covariance)과 상관계수(Correlation)의 개념이다.

Covariance

두 확률변수가 함께 얼마나 변하는지를 측정하는 지표

• 만약 한 변수의 큰 값들이 주로 다른 변수의 큰 값들과 대응되고, 작은 값들도 마찬가지로 대응된다면, 즉 두 변수가 비슷한 행동 패턴을 보이는 경향이 있다면, 공분산은 양수가 된다.
• 예시1) 키와 몸무게 (양의 공분산)
  • 키가 평균보다 큰 사람 → 몸무게도 평균보다 큼
  • 키가 평균보다 작은 사람 → 몸무게도 평균보다 작음
  • 같은 방향으로 움직임 = 양의 공분산
• 예시2) 운동 시간과 체중 (음의 공분산)
  • 운동 시간이 평균보다 많음 → 체중은 평균보다 적음
  • 운동 시간이 평균보다 적음 → 체중은 평균보다 많음
  • 반대 방향으로 움직임 = 음의 공분산

수학적 공식

• variance(분산): var(x) = E { (x - E(x))² }
  • E(x): x의 평균
  • (x - E(x)): 각 값이 평균에서 얼마나 떨어져 있는지
• Covariance(공분산): cov(x, y) = E { (x - E(x)) * (y - E(y)) }
  • (x - E(x)): x가 자기 평균에서 얼마나 벗어났는지
  • (y - E(y)): y가 자기 평균에서 얼마나 벗어났는지
  • 두 개를 곱함: 두 변수가 같은 방향으로 벗어났는지 확인

Limitation of covariance

• 크기 해석의 어려움
  • 공분산의 크기가 변수들의 변동성에 따라 달라진다.
  • case1) 변동성이 작은 경우
    • 변수들의 값이 평균 근처에 밀집되어 있으면 공분산의 최댓값도 작을 수밖에 없음
  • case2) 변동성이 큰 경우
    • 변수들의 값이 평균에서 멀리 퍼져 있으면 공분산의 최댓값이 커질 수 있음
  • 예시)
  • A: 키(cm)와 몸무게(kg)
    • cov = 150
  • B: 키(m)와 몸무게(kg)

    • cov = 1.5

      → 같은 관계이지만 단위만 바꿨을 뿐인데 공분산 값이 100배 차이가 난다. → 공분산 값만 보고는 얼마나 강한 연관성이 있는지 판단하기 어렵다.

Improvement idea for covariance

• 현재 공분산의 크기를 “최대 가능한 공분산”과 비교하여 평가 → 변동성의 크기에 상관없이 -1과 1사이의 표준화된 값을 얻을 수 있다.
  
• 최대 가능 공분산을 어떻게 결정할 것인가?
  • 각 변수가 가장 강하게 공변하는 대상은 자기자신이다.
  • cov(X,X) = Σ(X - Mₓ)(X - Mₓ) / N = var(X) → var(x)가 최대 공분산이다. (cov(X, X) = var(X) = σₓ²)
    

Covariance with itself

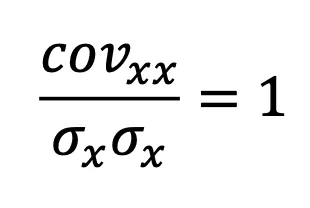
→ 만약 우리가 변수 자기 자신과의 공분산을 그 변수의 분산으로 나눈다면, 1이라는 값을 얻게 될 것이다.

→ 이것이 공분산의 크기(magnitude)를 평가하기 위한 표준(기준)이 된다.

Covariance between different variables

• X와 Y(서로 다른 변수) 간의 관계를 알고 싶다면
• 이때, 두 변수 간의 공분산은 두 변수의 표준편차를 곱한 값보다 클 수 없다. → $cov_{xy} \leq S_xS_y$
  
• 따라서 $S_xS_y$로 나눈다면 1을 기준으로 공분산의 크기를 평가할 수 있다. → $-1 \leq \frac{cov_{xy}}{S_xS_y} \leq 1$
  

Correlation

공분산을 표준화한 것을 Correlation(상관계수)라고 한다.

• $r = \frac{Σ(X - M_X)(Y - M_Y)}{(N × S_X × S_Y)}$

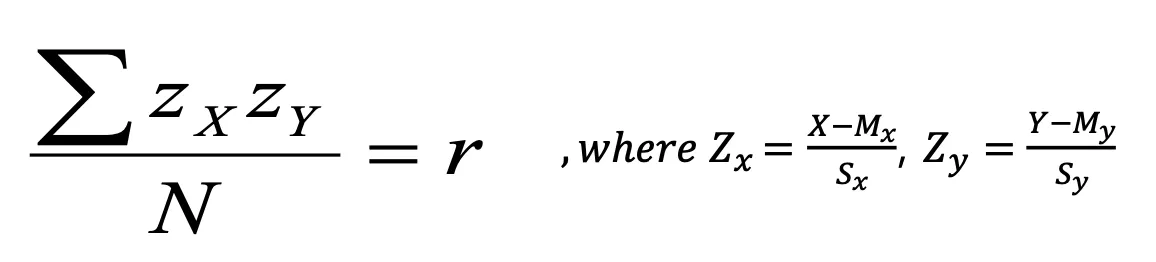
→ 두 공식이 동일하기 때문에, 상관계수는 z-score들의 곱의 평균으로도 정의될 수 있다.

→ 상관계수 r은 두 변수 간의 연관성을 나타내는 양적 지표이다. 이것은 z-score들의 곱들의 평균이다. 이 평균이 양수일 때는 양의 상관관계가 있고, 음수일 때는 음의 상관관계가 있다고 볼 수 있다.

→ 이것을 '피어슨 상관계수'라고 부른다.

• r의 값은 -1과 +1 사이의 범위를 가질 수 있다.
• r의 값은 -1과 +1 사이의 범위를 가질 수 있다.
• 만약 r = 1 (또는 -1)이면, 두 변수 간에 완벽한 양의 (또는 음의) 관계가 있다고 볼 수 있다.

차이점 정리

구분	공분산	상관계수
방향	알 수 있음	알 수 있음
강도	판단 어려움	명확함
범위	-∞ ~ +∞	-1 ~ +1
표준화	안됨	됨
비교	어려움	쉬움