Distance and Similarity

Similarity and Dissimilarity

• Similarity
  • 두 데이터 객체가 얼마나 비슷한지에 대한 수치적 측정값이다.
  • 객체들이 더 비슷할수록 (값이) 더 높다.
  • 보통 [0,1] 범위 안에 있다.
  • 근접도
• Dissimilarity
  • 두 데이터 객체가 얼마나 다른지에 대한 수치적 측정값이다.
  • 객체들이 더 비슷할수록 (값이) 더 낮다.
  • 최소 비유사도는 보통 0이다.
  • 상한선은 다양함 (경우에 따라 다름)
    

Common Properties

Distance

거리 함수가 만족해야 하는 3가지 속성

• 양의 정부호성 (Positive Definiteness)
  • 거리는 항상 0 이상이다.
  • 거리가 0이 되는 경우는 오직 두 점이 완전히 같을 때만
  • 예: 서울-부산 거리 ≥ 0, 서울-서울 거리 = 0
• 대칭성 (Symmetry)
  • A에서 B까지의 거리 = B에서 A까지의 거리
  • 방향과 무관하다.
  • 예: 서울→부산 거리 = 부산→서울 거리
• 삼각부등식 (Triangle Inequality)
  • 직접 가는 거리 ≤ 경유해서 가는 거리
  • 우회하면 더 멀거나 같다.
  • 예: 서울→부산 ≤ 서울→대전 + 대전→부산

Similarity

유사도 함수가 만족해야 하는 2가지 속성

• 최대 유사도 조건
  • 최대 유사도(보통 1)가 되는 경우는 오직 두 객체가 완전히 같을 때만
  • ex)
    • 나 자신과의 유사도 = 1 (최대)
    • 쌍둥이와의 유사도 = 0.95 (높지만 1은 아님)
    • 남과의 유사도 = 0.2 (낮음)
• 대칭성 (Symmetry)
  • A와 B의 유사도 = B와 A의 유사도
  • 방향과 무관하다.
  • ex) 철수가 보기에 영희와의 유사도 = 영희가 보기에 철수와의 유사도

Similarity Between Binary Vectors

Binary Vectors

• 각 속성이 0 또는 1만 가지는 벡터이다.
• 4가지 경우의 수

  	q = 0	q = 1
  p = 0	M₀₀	M₀₁
  p = 1	M₁₀	M₁₁

두 가지 유사도 측정 방법

Simple Matching (SM) - 단순 매칭 계수

SM = (M₁₁ + M₀₀) / (M₀₁ + M₁₀ + M₁₁ + M₀₀)
   = 일치하는 속성 / 전체 속성

• 특징
  • 0-0 일치도 중요하게 고려한다.
  • 전체 속성에서 일치하는 비율이다.
• 예시:
  • 두 사람 모두 "흡연 안 함(0-0)" → 일치로 카운트

→ 0과 1이 둘 다 중요한 경우 사용 / ex) 의학 검사 결과 (음성도 중요)

Jaccard Coefficient (J) - 자카드 계수

J = M₁₁ / (M₀₁ + M₁₀ + M₁₁)
  = 둘 다 1인 경우 / (적어도 하나가 1인 경우)

• 특징:
  • 0-0 일치는 무시한다.
  • 둘 다 없는 것(M₀₀)은 유사도에 영향이 없다.
• 예시:
  • 두 사람 모두 "흡연 안 함(0-0)" → 무시
  • 둘 다 "흡연 함(1-1)" → 중요하게 카운트

→ 1만 중요한 경우 / ex) 문서에 단어 존재 여부

SM vs. Jaccard: Example

→ 만약 영화 선호도라고 가정한다면 Jaccard가 더 적합한 상황이라고 볼 수 있다.

Minkowski Distance in Vector Data

• 유클리드 거리를 일반화 한 것이다.

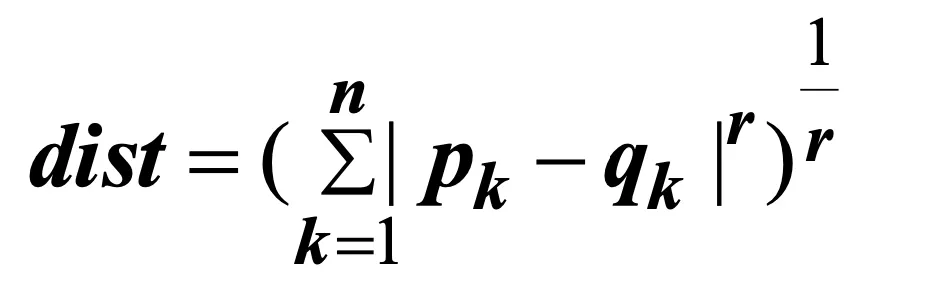
r = 1) 맨해튼 거리 ($L_1$ norm)

r = 2) 유클리드 거리 ($L_2$ norm)

r = max) 체비셰프 거리 ($L_{max}$ norm)

ex) (1,1)에서 (4,3)까지의 거리

• $L_1$ norm → |4-1|+|3-1| → 5
• $L_2$ norm → √((4-1)²+(3-1)²) → 3.6
• $L_{max}$ norm → max(|4-1|,|3-1|) → 3

Euclidean distance vs Cosine similarity

• 유클리드 거리: 기하학적 거리를 본다.
• 코사인 유사도: 방향을 본다.

Euclidean distance

• 두 점 사이의 직선 거리
• ex) (4,3),(1,1) → √((4-1)² + (3-1)²) = √13 ≈ 3.6

Cosine similarity

• 각도의 유사성
  

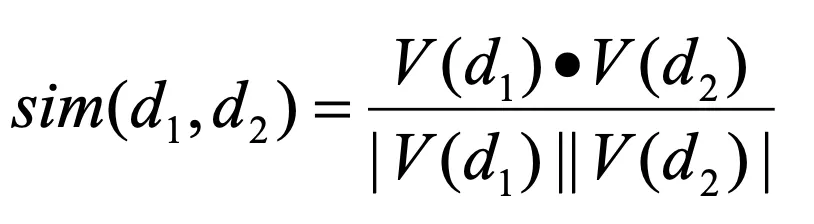
• 유사도 = 두 벡터 사이 각도의 코사인 값
  • 각도가 작으면 (방향이 비슷) → 유사도 높음
  • 각도가 크면 (방향이 다름) → 유사도 낮음
• 특징:
  • 방향만 중요하다.
  • 위치나 크기는 무시 / 크기에 영향을 받지 않음

Distance Between Sequence Data

Levenshtein Distance

• Edit Distance(편집거리)라고도 불린다.
• 두 문자열을 같게 만들기 위해 필요한 최소 편집(삽입, 삭제, 교체) 횟수
• 예시 1) kitten → sitting
• 단계별 변환:

  1. kitten → sitten   (k를 s로 교체)
  2. sitten → sittin   (e를 i로 교체)
  3. sittin → sitting  (끝에 g 삽입)

  → 총 편집 횟수 = 3 / 레벤슈타인 거리 = 3