1.학습한 내용

#normalization 일반화 = 데이터에 scale을 조정하는 작업(샘플링, 스켈링 등)
#Regularization 정규화 = 규칙제어, predict funtion에 복잡도를 조정하는 작업

#L1 ,L2 제약
#Lasso L1, Ridge L2
#L1 => 제약을 걸면 걸수록 약한 값들은 0에 가까워 진다
#L2 => feature들의 전체의 속성에 대해서 전반적인 제약을 건다, 속성들이 0이 되지는 않는다
#데이터들에 어떤 것들이 더 효과적인지에 대해서는 직접 해보는 수 밖에 없다
#일반적으로 릿지제약이 라쏘제약보다 성공할 확률이 높다(절대적이진 않다)

logreg100 = LogisticRegression(max_iter=5000, C=100).fit(X_train, y_train)
print(logreg100.score(X_train, y_train))
print(logreg100.score(X_test, y_test))
0.9788732394366197
0.965034965034965
#C값이 크면 클수록 오류를 허용하지 않겠다는 것을 의미

logreg001 = LogisticRegression(max_iter=5000, C=0.01).fit(X_train, y_train)
print(logreg001.score(X_train, y_train))
print(logreg001.score(X_test, y_test))
0.9460093896713615
0.972027972027972
#데이터의 오류의 제약을 풀어서 새로운 데이터에 대한 적응력을 높여 정확도를 높일 수 있다

from sklearn.datasets import make_blobs
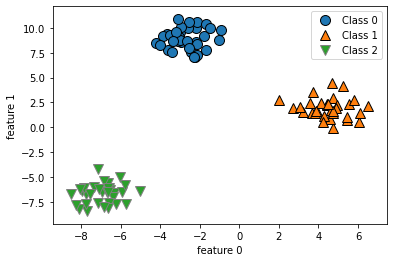
X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:,0], X[:,1], y)
plt.xlabel('feature 0')
plt.ylabel('feature 1')
plt.legend(['Class 0', 'Class 1', 'Class 2'])
#3가지 그룹에 대한 데이터를 분류

linearsvm = LinearSVC().fit(X, y)
print(linear_svm.coef)
print(linearsvm.intercept)
#coef = 기울기 , intercept = 절편
#'회귀'라면 선형 회귀가 하나가 있는게 일반적 y = xw + b
#y = x1w1 + x2w2 + x3w3 + b => 선이 세개가 필요

mglearn.plots.plot2d_classification(linear_svm, X, fill=True, alpha=0.7)
mglearn.discrete_scatter(X[:,0],X[:,1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef,
linearsvm.intercept,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
#line=x, coef=w, intercept=b
#가운데 점을 기점으로 나누어 줄 수 있다고 생각해본다면
#이 집합(class)가 많아지기 시작하면 분류를 하기 힘들어 진다

#좀 더 복잡한 문제가 나온다면 선형회귀는 정확도가 많이 떨어진다
#Tree 계열 분류 알고리즘
mglearn.plots.plot_tree_progressive()

from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=42)
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
#의사결정나무
print(tree.score(X_train, y_train))
print(tree.score(X_test, y_test))
1.0
0.9300699300699301

tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)
print(tree.score(X_train, y_train))
print(tree.score(X_test, y_test))
#데이터에 과도하게 접합되는걸 막기위해 max_depth설정
0.9953051643192489
0.951048951048951

from sklearn.tree import plot_tree

plot_tree(tree, class_names=['A','B'], filled=True, fontsize=4,
feature_names=cancer.feature_names)

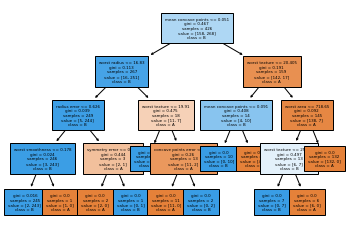
print(tree.featureimportances)
#각 트리의 중요도를 확인
#보통 depth를 계속 변경해보며(3~20) 최적의 값을 찾아본다

import os
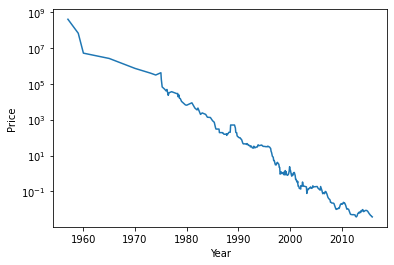
ram_price = pd.read_csv('data/ram_price.csv')
plt.semilogy(ram_price.date, ram_price.price)
plt.xlabel('Year')
plt.ylabel('Price')
#간단한 그래프 semilogy

#CSP업체들 => 다수의 클라우드들을 판매하는 업체들(수수료, 기술지원)
#메가존, 글루코스, 베스핀 글로벌
#지금 배우는 내용들은 30년 전의 이론들

from sklearn.tree import DecisionTreeClassifier
data_train = ram_price[ram_price.date < 2000]
data_test = ram_price[ram_price.date >= 2000]

#pandas 시리즈 객체 => 넘파이 객체로 바꿔줘야 한다
#numpy 배열에서 축을 하나 늘려주는 명령 = newaxis
data_train.date.to_numpy()[:,np.newaxis]

X_train = data_train.date.to_numpy()[:,np.newaxis]
y_train = np.log(data_train.price)
#log함수는 데이터의 변별력을 높이기 위해 사용하는 기법
#log함수는 0에 가까울 수록 변화의 폭이 크지 않다가 y의 값이 커질수록 x의 값이 크게 커진다
#시그모이드 함수의 형태 = 변별력을 높일 때

from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
tree = DecisionTreeRegressor().fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)

X_all = ram_price.date.to_numpy()[:,np.newaxis]
#새로 만든 X축 = 전체 날짜 값만 다 들어 있다

pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)
#X로 예측한 price가 나온다

price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)
#log로 변환한 값을 돌려놓을 수 있다 => exp함수 사용

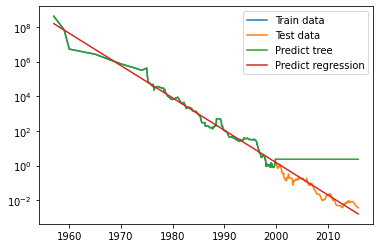
plt.semilogy(data_train.date, data_train.price, label='Train data')
plt.semilogy(data_test.date, data_test.price, label='Test data')
plt.semilogy(ram_price.date, price_tree, label='Predict tree')
plt.semilogy(ram_price.date, price_lr, label='Predict regression')
plt.legend()
#오차들을 모아서 학습하는게 MAE
#tree 알고리즘의 한계치

#RandomForestClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
#noise 약간의 오차를 생성

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
forest = RandomForestClassifier(n_estimators=5, random_state=2)
forest.fit(X_train, y_train)
#n_estimators의 기본값은 100

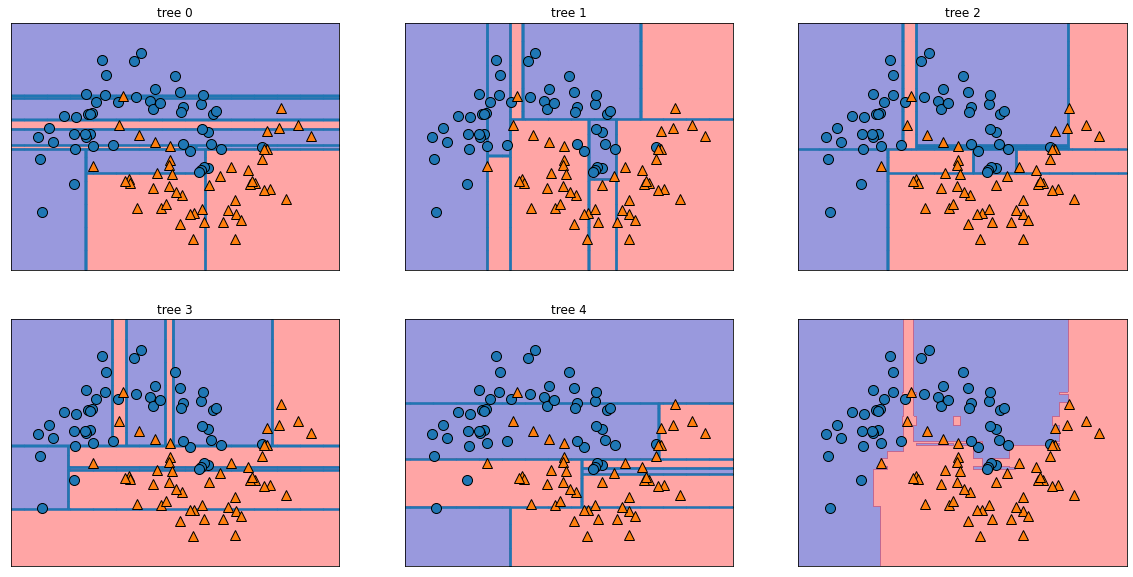
fig, axes = plt.subplots(2,3, figsize=(20,10))
for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)):
ax.set_title('tree {}'.format(i))
mglearn.plots.plot_tree_partition(X, y, tree, ax=ax)

mglearn.plots.plot_2d_separator(forest, X, fill=True, ax=axes[-1,-1],
alpha=0.4)
mglearn.discrete_scatter(X[:,0],X[:,1], y)
#그래프에 숫자 매기기 , enumerate = 열거형
#풀만큼 풀었기 때문에 정확도가 높다
#random forest알고리즘이 그린 다섯가지 그림을 합쳐서 6번째 그림을 그린 것
#데이터의 모집합이 큰 것들의 경우 데이터의 일반화가 잘된다
#유튜브의 경우 수많은 알고리즘이 분석해서 통과하는 것들만 업로드가 가능하다
#facebook같은 경우 이런 분석 알고리즘들이 매우 취약하다, 때문에 문제들 많음

X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=0)
forest = RandomForestClassifier(n_estimators=100, random_state=0)
forest.fit(X_train, y_train)
#얼마나 정확한가에 대한 평가
print(forest.score(X_train, y_train))
print(forest.score(X_test, y_test))
1.0
0.972027972027972

from sklearn.ensemble import GradientBoostingClassifier #GB

X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=0)
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train)
print(gbrt.score(X_train, y_train))
print(gbrt.score(X_test, y_test))
1.0
0.965034965034965

gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)

print(gbrt.score(X_train, y_train))
print(gbrt.score(X_test, y_test))
0.9906103286384976
0.972027972027972
#제약을 걸었더니 테스트정확도가 오르고 학습정확도는 떨어졌다
#GradientBoost는 내부적으로 오차를 보정하는 기능이 포함되어 있기 때문에
#깊게 들어가지 않아도 정확도가 높다
#depth를 적게쓰고 정확도가 높다는 것은 메모리를 적게 쓰고 문제를 해결할 수 있다
#보통 4~5단계에서 대부분 해결이 된다
#GradientBoosting은 depth와 learning_rate를 제어할 수 있다

gbrt = GradientBoostingClassifier(random_state=0, learning_rate=0.1)
gbrt.fit(X_train, y_train)
print(gbrt.score(X_train, y_train))
print(gbrt.score(X_test, y_test))
1.0
0.965034965034965
#학습하는 정도를 제약을 걸 수 있다
#learning_rate를 지정하게 되면 학습하는 정도를 지정할 수 있다(복잡도 제어)

X, y = make_blobs(centers=4, random_state=8)
#2차원 배열, 4개의 데이터가 나오는 집합
y = y % 2
#%는 나머지를 버리는 것
mglearn.discrete_scatter(X[:,0], X[:,1], y)
plt.xlabel('feature 0')
plt.xlabel('feature 1')
#이 그룹을 2개의 그룹으로 만들고 싶다
#0 1 2 3을 짝수, 홀수로 묶으면 된다
#일반적인 선형회귀로는 해결이 안된다
#어떻게 해도 선으로 잘 갈라지지 않는다
#이럴 때 개념적으로 접근하는 방법이 SVM(support vector machine)

2. 학습내용 중 어려웠던 점

-확실히 그냥 학습하는 것 보다 변수들을 적용했을 때 변화하는 점을 비교해보는게 이해하는데 도움이 되는 것 같다. 어제, 오늘 내용들이 정말 쉽지 않은 것 같다. 어떨때 쓰이는지 변수는 어떻게 적용되어야 하는지는 따라갈 수 있지만 이런 경우 혼자서 다 해보라고 하면 정말 어려울 것 같다.

3. 해결방법

-주피터 노트북에 만들어놓은 내용들을 몇 번씩 반복해 보는 것 말고는 방법이 없는 것 같다. 이해하기 쉽지 않지만 관념적으로 일단 이런게 있고, 이렇게 사용한다는 식으로 최대한 이해해봐야겠다.

4. 학습소감

-학습양도 양이지만 이해하기가 정말 쉽지 않다. 언제쯤이면 이건 이거구나라면서 다 이해하는 날이 올까 바라게된다. 그러니 지치지말자.