1.학습한 내용

#알고리즘을 경험적으로 이해하고 쌓아가는게 아주 중요하다

X_new = np.hstack([X, X[:, 1:] ** 2])

from mpl_toolkits.mplot3d import Axes3D, axes3d
figure = plt.figure()

#3차원 그래프
ax = Axes3D(figure, elev=-152, azim=-26)
#y == 0 인 포인트를 먼저 그리고 그 다음 y == 1 인 포인트를 그립니다
mask = y == 0
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
cmap=mglearn.cm2, s=60, edgecolor='k')

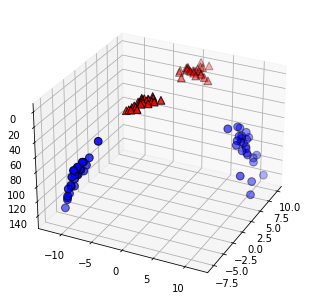
#SVM의 가장 중요한 개념 = 결정 경계(Decision Boundary) = 분류를 위한 기준 선을 정의하는 모델
#속성이 늘어나면 즉, 3차원 이상으로 늘어난 고차원 = 초평면(hyperplane)
#결정 경계는 데이터 군으로부터 최대한 멀리 떨어지는 게 좋다
#Support Vectors는 결정 경계와 가까이 있는 데이터 포인트들을 의미한다
#이 데이터들이 경계를 정의하는 결정적인 역할을 하는 셈
#마진(Margin)은 결정 경계와 서포트 벡터 사이의 거리를 의미
#최적의 결정 경계는 마진을 최대화한다
#SVM에서는 결정 경계를 정의하는 게 결국 서포트 벡터이기 때문에
#데이터 포인트 중에서 서포트 벡터만 잘 골라내면 나머지 쓸 데 없는 수많은 데이터 포인트들을 무시할 수 있다
#그래서 매우 빠르다
#이상치(outlier)를 잘 다루는 게 중요
#하드 마진(hard margin) = 서포트 벡터와 결정 경계 사이의 거리가 매우 좁다, 마진이 매우 작아진다. 이렇게 개별적인 학습 데이터들을 다 놓치지 않으려고 아웃라이어를 허용하지 않는 기준으로 결정 경계를 정해버리면 오버피팅(overfitting) 문제가 발생할 수 있다.
#소프트 마진(soft margin) = 서포트 벡터와 결정 경계 사이의 거리가 멀어졌다,마진이 커진다. 대신 너무 대충대충 학습하는 꼴이라 언더피팅(underfitting) 문제가 발생할 수 있다.
#scikit-learn에서는 SVM 모델이 오류를 어느정도 허용할 것인지 파라미터 C를 통해 지정할 수 있다. (기본 값은 1이다.)
#C값이 클수록 하드마진(오류 허용 안 함), 작을수록 소프트마진(오류를 허용함)이다

X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=0)
from sklearn.svm import SVC
svc = SVC()
svc.fit(X_train, y_train)

print(svc.score(X_train, y_train))
print(svc.score(X_test, y_test))
0.903755868544601
0.9370629370629371
#정확도 분석
#3차원의 일부를 학습 => 초평면 => 높은 정확도
#데이터의 군집이 높은 데이터들은 정확도가 높을 수 있다
#데이터의 군집이 낮은 데이터들은 tree를 쓰는게 효율적일 수 있다
#실제로 부동산업계에서 많이 사용한다
#우리나라 전체 지도에서 부동산 가격이 높은 분포들을 잘라서 나타낼 수 있다

TensorFlow

#구글, google, 핵심코드 = C++
#직관적인 API
#뛰어난 이식성 및 확장성
#진입 장벽이 높다

Keras

#tensorFlow를 backend로 사용

Pythorch

#페이스북
#GPU가속연산
#진입장벽이 낮음, 파이썬 문법과 유사
#C/CUDA Backend로 사용

Deel Learning을 위한 수학

딥러닝을 구성하는 기본적인 것들에 대해서 알아보자
일차함수 = y = ax + b(a=기울기, b=절편, 직선 그래프 linear)
#linear Function 일차함수를 파이썬으로 만들어보자

import math
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')

def linear_function(x):
a = 0.5
b = 2
return a * x + b
#함수 만들기
#수식을 보고 풀어보면 그다지 어렵지 않다

print(linear_function(5))
#bector값을 준다 = 특정한 길이의 배열을 준다
#전체 값을 계산해 준다
#파이썬만의 편리함

x = np.arange(-5,5,0.1)
y = linear_function(x)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Linear Function')

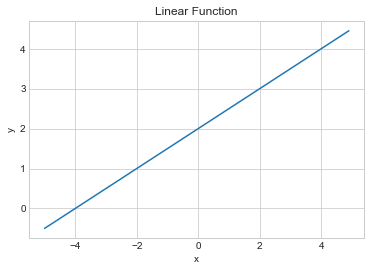
이차함수 = y =ax2 + bx + c (일반적으로 두 개의 실근을 가짐)

삼차함수 = y = ax3 + bx2 + cx + d

이차함수를 만들어 보자

def quadratic_function(x):
a = 1
b = -2
c = -2
return a x**2 + b x + c

x = np.arange(-5,5,0.1)
y = quadratic_function(x)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Quadratic Function')
#수식을 연산자로 나열만 하면 쉽게 만들 수 있다

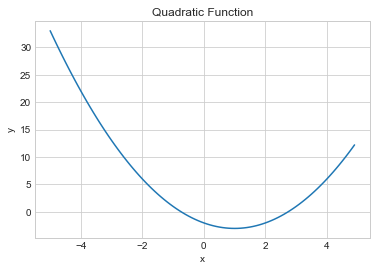
삼차함수를 만들어 보자

def cubic_function(x):
a = 4
b = 0
c = -1
d = -8
return a x**3 + b x*2 + c x + d

x = np.arange(-5,5,0.1)
y = cubic_function(x)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Cubic Function')

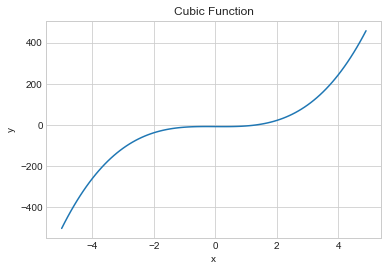
#함수의 최소값/최대값
#지수함수(제곱으로 늘어나는 값)/로그함수 = 역함수 관계 (개도국 <=> 선진국)
#지수,로그함수 만나는 점 = 교착점 => 최적점을 찾을 활용
#미분 = 어떤 함수를 나타내는 그래프에서 한 점의 미분값(미분계수)을 구하는 것은 해당 점에서의 접선을 의미
#기울기는 방향성을 가짐
#편미분 = 변수가 1개짜리인 위의 수치미분과 달리, 변수가 2개 이상일 때의 미분법
#다변수 함수에서 특정 변수를 제외한 나머지 변수는 상수로 처리하여 미분
#수학적 구현이 가능하다는 것을 알아두자

신경망 데이터 표현

#텐서(Tensor)
#데이터 하나 하나를 Tensor 라고 부름
#모양에 따라 Tensor의 이름이 달라진다
#한 개 = Scalar(0차원 tensor)
#방향성이 생긴 여러개 = vector(1차원 tensor)
#vector가 많아져서 방향성이 많아지면 = 2D vector
#한 면이 더 생기면 = 3D vector (사람이 인지 할 수 있는 한계)
#1D vector = shape(x,)
#2D vector = shape(x,y)
#3D vector = shape(x,y,z)
#.......이렇게 늘어간다
#tensor를 코드로 구현해보자

#0차원 텐서 = 스칼라
x = np.array(3)
print(x)
#3이라는 숫자가 들어간 하나의 배열
print(x.shape)
#방향, 차원이 없기 때문에 괄호만 나온다
print(np.ndim(x))
#차원 개수 표현
3
()
0

#1차원 텐서
a = np.array([1,2,3,4])
b = np.array([5,6,7,8])
#텐서들은 같은 차원이면 함께 처리되는 성격이 있다
c = a + b
print(c)
#같은 자리에 있는 텐서들끼리 연산되어 결과가 나왔다
print(c.shape)
print(np.ndim(c))
#4개의 값 ,1차원
6 8 10 12
1

m = np.array(10)
d = a * m
print(d)
#m이라는 스칼라의 개수가 부족한만큼 자기복제해서 a라는 함수 개수에 맞춰 연산되었다
#이를 Broadcasting, casting 라고 한다
[10 20 30 40]

#2차원 텐서의 곱셈
a = np.array([[1,2],[3,4]])
print(a)
print(a.shape)
print(np.ndim(a))
#2개의 값, 2차원
b = np.array([[10,10],[10,10]])
print(a * b)
#같은 차원의 값끼리 연산이 되었다
[[1 2][3 4]]
(2, 2)
2
[[10 20][30 40]]

#전치행렬을 알아보자
a = np.array([[1,2,3],[4,5,6]])
#다른 모양으로 바꾸어 보자 => 전치행렬 T (피봇)
a = a.T
print(a)
[[1 4][2 5]
[3 6]]

X = np.array([[[5,3,2,1],
[5,5,3,1],
[6,1,2,3]],
[[1,1,1,1],
[3,4,7,5],
[1,8,3,4]],
[[10,9,3,9],
[5,4,3,2],
[7,6,3,4]]
])
#[]가 몇개 열린가에 따라 차원 수를 알 수 있다
print('X\n', X, end='\n\n')
print('X.shape:', X.shape)
print('X.ndim:', X.ndim)
#3개의 차원, 3개의 그룹, 4가지 텐서
X
[[[ 5 3 2 1][ 5 5 3 1]
[ 6 1 2 3]]

[[ 1 1 1 1][ 3 4 7 5]
[ 1 8 3 4]]

[[10 9 3 9][ 5 4 3 2]
[ 7 6 3 4]]]

X.shape: (3, 3, 4)
X.ndim: 3

MNIST 손글씨 이미지

pip install tensorflow
pip install mnist

from keras.datasets import mnist

(X_train, y_train), (X_test, y_test) = mnist.load_data()

print(X_train.shape)
print(X_train.ndim)
(60000, 28, 28)
3

print(X_train.dtype)
uint8
#8비트 정수형이다 u = -가 없는 정수형이다, 2**8 = 256가지를 표현할 수 있다

temp_image = X_train[3]

#화면에 보여주기
plt.imshow(temp_image, cmap='gray')
#60000 / 24 => 2500 /60 => 41분짜리 영상으로 표현 가능(흑백)

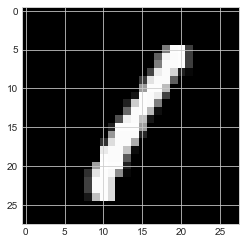
#컬러 이미지 = 4차원
#동영상 = 5차원

신경망 구조

#퍼셉트론
#인공신경망의 한 종류
#다수의 입력과 가중치를 곱하여 그 값에 편향을 더한 값이 어느 임계치값을 초과하면 활성화 함수(activation function)를 통과

#논리회로
#논리 게이트(logic gates)
#AND OR NOT NAND(not and) NOR(not or)

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')

AND gate만들기

def AND(x1, x2):
input = np.array([x1, x2])
weights = np.array([0.4,0.4])
bias = -0.6

value = np.sum(input * weights) + bias

if value <= 0:
return 0
else:
return 1
#weight, bias 값을 바꿔서 새로운 logic을 만들 수 있다

print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))
0
0
0
1

x1 = np.arange(-2, 2, 0.01)
x2 = np.arange(-2, 2, 0.01)
bias = -0.6

y = (-0.4 * x1 - bias) / 0.4

plt.axvline(x=0) #수직
plt.axhline(y=0) #수평

plt.plot(x1, y, 'r--') #레드, 대쉬선
plt.scatter(0,0,color='orange',marker='o',s=150)
plt.scatter(0,1,color='orange',marker='o',s=150)
plt.scatter(1,0,color='orange',marker='o',s=150)
plt.scatter(1,1,color='black',marker='^',s=150)
plt.xlim(-0.5,1.5)
plt.ylim(-0.5,1.5)
plt.grid()
#신경망 세포에서 했던 계산

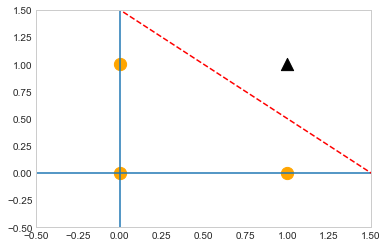
수치만 바꿔보면 or gate를 만들 수 있다

def OR(x1, x2):
input = np.array([x1, x2])
weights = np.array([0.4,0.4])
bias = -0.3

value = np.sum(input * weights) + bias

if value <= 0:
return 0
else:
return 1
#기본 편향치를 낮춰주면 or조건이 된다
#동일한 세포를 다양하게 변환해서 사용할 수 있다

print(OR(0,0))
print(OR(0,1))
print(OR(1,0))
print(OR(1,1))
0
1
1
1

x1 = np.arange(-2, 2, 0.01)
x2 = np.arange(-2, 2, 0.01)
bias = -0.3

y = (-0.4 * x1 - bias) / 0.4

plt.axvline(x=0) #수직
plt.axhline(y=0) #수평

plt.plot(x1, y, 'r--') #레드, 대쉬선
plt.scatter(0,0,color='black',marker='^',s=150)
plt.scatter(0,1,color='orange',marker='o',s=150)
plt.scatter(1,0,color='orange',marker='o',s=150)
plt.scatter(1,1,color='orange',marker='o',s=150)
plt.xlim(-0.5,1.5)
plt.ylim(-0.5,1.5)
plt.grid()

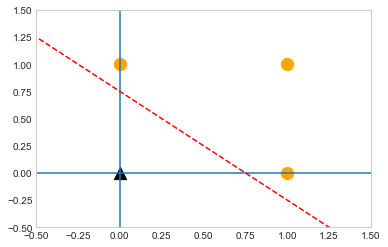
NAND gate

def NAND(x1, x2):
input = np.array([x1, x2])
weights = np.array([-0.6,-0.6])
bias = 0.7

value = np.sum(input * weights) + bias

if value <= 0:
return 0
else:
return 1

print(NAND(0,0))
print(NAND(0,1))
print(NAND(1,0))
print(NAND(1,1))
1
1
1
0

XOR게이트=> 신경망을 늘려서 해결(다층 퍼셉트론multi layer perceptron,MLP)

#여러개의 신경망을 사용하는 다층 퍼셉트론
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y

print(XOR(0,0))
print(XOR(0,1))
print(XOR(1,0))
print(XOR(1,1))
0
1
1
0

#tensorflow, keras에 다 구현이 되어있다
import keras
keras.version

#Dense layer 가장 기본적인 형태의 신경망
#신경망을 설계할 때 세포 하나 하나를 설계하지 않는다
#뉴럴을 몇개나 집어넣을 것인가, 몇개의 레이어를 사용할 것인가를 결정
#나머지는 keras에서 알아서 결정해서 만들어준다

from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
#원하는 mnist데이터 불러오기

train_images.shape
(60000, 28, 28)
#60000개, 28x28 이미지

train_labels.shape
(60000,)

test_images.shape
(10000, 28, 28)

digit = train_images[4]
plt.imshow(digit, cmap='gray')

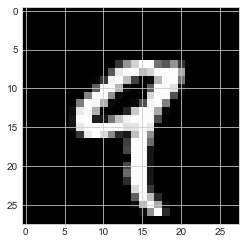
print(train_labels[4])
9

from keras import models
from keras import layers

network = models.Sequential()
#하나의 신경망을 시작하기 위한 코드의 시작
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
#첫 번째 레이어의 완성
network.add(layers.Dense(10, activation='softmax'))
#출력이 나오는 레이어

2. 학습내용 중 어려웠던 점

-수학적 공식을 데이터화하는 법을 실습했다. 확실히 따라하는 것은 어렵지 않았고, 생각보다 간단한 수학공식들이었기에 데이터화 하는게 어렵지 않았다.

3. 해결방법

-공식이 어려워지면 코딩화 하는게 쉽지 않을 것 같다. 무엇보다 딥러닝의 영역은 미분이 필수라고 하는데 미분에 대해서 하나도 모르니 걱정이다. 때문에 정말 EBS에 미분에 관한 부분을 찾아봐야 할 것 같다. 기본적인 부분은 알아야 한다고 하니 공부해 봐야겠다.

4. 학습소감

-오늘 코딩은 따라가기 어렵지 않았지만 미분에 관한 부분은 걱정이 된다. 배워야할 것들이 넘쳐나니 어쩔줄을 모르겠는 부분도 있다. 빠르게 내가 노려야할 부분을 정할 수 있으면 정한 뒤 집중할 수 있게 찾아야겠다.