인공지능 수학 - 확률과 확률분포
확률(Probability)
-
상대 도수에 의한 정의
- 똑같은 실험을 무수히 많이 반복할 때 어떤 일이 일어나는 비율
- 상대도수의 극한 -
고전적 정의
- 표본공간: 모든 가능한 실험결과들의 집합
- 사건: 관심있는 실험결과들의 집합(표본공간의 부분집합)
- 어떤 사건이 일어날 확률(표본공간의 모든 원소가 일어날 확률이 같은 경우): 사건의 원소의 수 / 표본공간의 원소의 수 -
확률의 계산
- 조합(combination): 어떤 집합에서 순서에 상관없이 뽑은 원소의 집합, nCr = n! / r! * (n - r)! -
확률 법칙
- 덧셈 법칙: P(A∪B) = P(A) + P(B) - P(A∩B)
- 서로 배반(Mutually Exclusive): 두 사건의 교집합이 공집합인 경우, P(A∪B) = P(A) + P(B)
- 곱셈 법칙: P(A∩B) = P(B|A)P(A)
- 서로 독립: P(B|A) = P(B)인 경우, P(A∩B) = P(A)P(B)
-
조건부 확률(Conditional Probability)
- 어떤 사건 A가 일어났을 때, 다른 사건 B가 일어날 확률
- P(B|A) = P(A∩B) / P(A) (단, P(A) > 0)
- 표본공간의 변화로 생각하자! -
확률의 분할 법칙
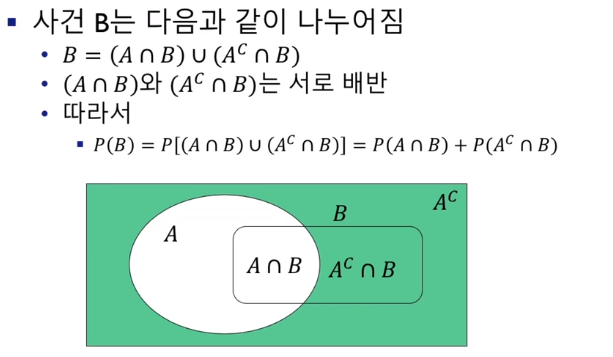
- P(B) = P(A∩B) + P(A^c∩B) = P(B|A)P(A) + P(B|A^c)P(A^c)
-
베이즈 정리
- 추론 대상의 사전확률(prior probability)과 추가적인 정보를 통해 해당 대상의 사후확률(posterior probability)을 추론하는 방법
- 사전 확률 P(A): 결과가 나타나기 전에 결정되어 있는 원인 "A"의 확률
- 사후 확률 P(A|B): B가 발생 시 조건하에서 "A"가 발생하는 확률
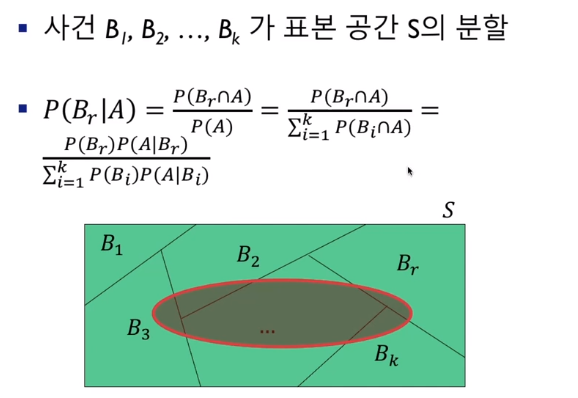
- P(A|B) = P(A∩B) / P(B) = P(B|A)P(A) / P(B)
확률 분포(Probability Distribution)
-
확률 변수(Random Variable)
- 랜덤한 실험 결과에 의존하는 '실수', 즉 표본 공간의 부분 집합에 대응하는 실수
- 보통 표본 공간에서 실수로 대응되는 함수로 정의하며 X나 Y같은 대문자로 표시
-이산확률변수: 확률변수가 취할 수 있는 모든 수 값들을 하나씩 셀 수 있는 경우(ex. 주사위를 굴려 나온 숫자)
-연속확률변수: 셀 수 없는 경우(ex. 어느 학교에서 랜덤하게 선택된 남학생의 키) -
확률 분포(Probability Distribution)
- 확률 변수가 가질 수 있는 값에 대해 확률을 대응시켜주는 관계
- 확률 변수 X도 평균과 분산을 가지며 이 평균과 분산을 모집단의 평균과 분산이라고 할 수 있다.
-
이산확률변수(Discrete Random Variable)
- 평균(기대값, expected value):E(X) = ΣxP(X = x) = Σxf(x)
- 분산: (X - μ)^2의 평균,Var(X) = σ^2 = Σ(xi - μ)^2 / N = E(X^2) - {E(X)}^2
- 표준편차: 분산의 양의 제곱근,SD(X) = σ -
결합확률 분포(Joint Probability Distribution)
- 두 개 이상의 확률 변수가 동시에 취하는 값들에 대해 확률을 대응시켜주는 관계
- 결합확률 분포를 통해 각 확률 변수의 확률 분포를 도출할 수 있다. (주변확률분포, marginal probability distribution)
-
공분산(Covariance)
- 확률변수 X와 Y의 공분산: (X - μx)(Y - μy)의 평균
-Cov(X,Y) = E[(X - μx)(Y - μy)] = E(X)(Y) - μxμy = E[XY] - E[X]E[Y]
-
상관계수(Correlation Coefficient)
- 공분산은 각 확률 변수의 절대적인 크기에 영향을 받으므로 단위에 의한 영향을 없앨 필요가 있다.
-ρ = Corr(X,Y) = Cov(X,Y) / σxσy
이항분포(Binomial Distribution)
-
베르누이 시행(Bernoulli Trial)
- 정확하게 2개의 결과만을 가지는 실험(ex. 동전 던지기)
- 보통 성공과 실패로 결과를 구분, 성공의 확률을 p라고 한다. -
이항분포
- n번의 베르누이 시행에서 성공의 횟수를 확률변수 X라고 할 때, 이는 이항확률변수이다.
- 이항분포는 이항확률변수의 확률분포이다.
- 이항확률변수 X의 확률분포

- 평균:E(X) = np
- 분산:Var(X) = np(1 - p)
정규분포(Normal Distribution)
-
정규분포
- 연속확률변수의 확률분포는 확률밀도함수(probability density function)으로 나타낸다.
- P[a ≤ X ≤ b] = ∫f(x)dx (적분 범위는 a부터 b까지)
- 정규분포의 확률밀도함수
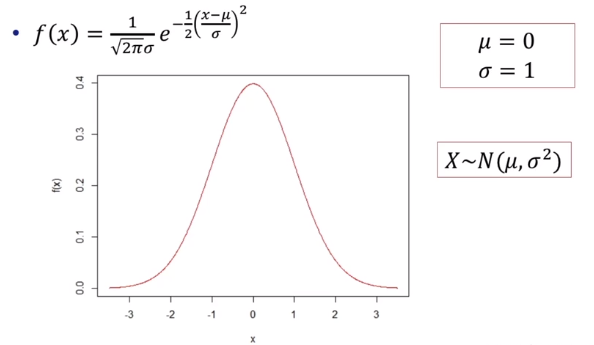
-
표준정규분포(Standard Normal Distribution)
- 정규화: Z = (X - μ) / σ
- 표준정규확률변수 Z는 평균이 0, 표준편차가 1인 정규분포를 따른다.
포아송 분포(Poisson Distribution)
- 포아송 분포
- 일정한 시간 단위 또는 공간 단위에서 발생하는 이벤트의 수의 확률분포(ex. 하루 동안 어떤 웹사이트를 방문하는 방문자의 수)
- 포아송 분포의 확률분포함수(확률질량함수)
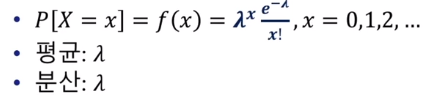
- 지수분포(Exponential Distribution)
- 포아송 분포에 의해 어떤 사건이 발생할 때, 어느 한 시점으로부터 이 사건이 발생할 때까지 걸리는 시간에 대한 확률 분포
- 포아송 분포의 확률밀도함수

