[TIL Day12] 인공지능 수학 - 추정, 검정, 엔트로피

인공지능 수학 - 추정, 검정, 엔트로피

표본분포(Samplind Distribution)

통계량의 확률분포

• 표본조사
  - 표본조사를 통해 파악하고자 하는 정보는 '모수'(모평균, 모분산, 모비율 등)
  - 모수를 추정하기 위해 표본을 선택하여 표본평균이나 표본분산 등 계산
  - 표본평균이나 표본분산과 같은 표본의 특성값을 통계량이라고 한다.
  - 표본의 평균은 표본의 선택에 따라서 달라지므로, 표본평균은 확률변수이다. 따라서 표본평균이 가질 수 있는 값도 하나의 확률분포를 가진다.

• 표본평균의 분포
  - 표본평균: 모평균을 알아내는데 쓰이는 통계량, ˉx = Σxi / n
  - 정규모집단에서 추출된 표본의 측정값에 대해 표본평균은 평균이 μ이고 분산이 σ^2/n인 정규분포를 따른다. ˉX ~ N(μ, σ^2/n)

• 중심극한정리(Central Limit Theorem)
  - (정규분포를 따르지 않는, 임의의)모집단에서 추출된 표본의 측정값에 대해 표본크기 n이 충분히 큰 경우(n >= 30), 표본평균은 근사적으로 평균이 μ이고 분산이 σ^2/n인 정규분포를 따른다.
  

추정(Estimation)

표본을 통해 모집단 특성이 어떠한가에 대해 추측하는 과정이다.

• 모평균의 추정
  - 모집단이 정규분포인경우: 표본평균 사용

  • 대표본인경우: 중심극한정리에 의해 표본평균이 정규분포를 따른다고 가정

• 모평균의 점추정
  - 표본평균이 점 추정값(추정량)이 된다.
  

• 모평균의 구간추정
  - 모평균 μ의 100(1 - α)% 신뢰구간(confidence interval): 표본평균과 표본표준편차로 제시한 신뢰구간 안에 실제 모평균이 포함될 확률이 100(1 - α)%이라는 의미이다.
  - 모평균이 정규분포를 따르고 모표준편차 σ를 알고 있을 때의 신뢰구간
  
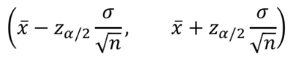
  - 정규분포가 아니거나 표준편차가 알려져 있지 않을 경우 실용적이지 못하다.
  - 모집단의 분포를 모르지만 표본의 크기가 클 때는 중심극한정리를 적용한다. 모표준편차 대신 표본표준편차 s를 사용한다.
  

• 모비율의 점추정
  - 확률변수 X를 n개의 표본에서 특정 속성을 갖는 표본의 개수라고 하자.
  - 모비율 p의 점추정량: p^ = x / n
  

• 모비율의 구간추정
  - 표본크기 n이 충분히 클 때(np^ > 5, n(1 - P^) > 5일 때를 의미) 확률변수 X의 정규분포를 가정할 수 있으며, X ~ N(np, np(1 - p))
  - 확률변수 X의 표준화(근사적으로 표준정규분포를 따름)
  
  - 모비율 p의 100(1 - α)%의 신뢰구간
  
  

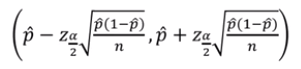
가설검정(Testing Hypothesis)

모집단 실제값이 얼마나 되는가 하는 주장과 관련해서, 표본이 가지고 있는 정보를 이용해 가설이 올바른지 그렇지 않은지 판정하는 과정을 나타낸다.

• 통계적 가설검정
  - 표본평균 ˉX가 μ0보다 얼마나 커야 모평균 μ가 μ0보다 크다고 할 수 있을 것인가?
  - 귀무가설 H0: μ = μ0
  - 대립가설 H1: μ > μ0
  - 귀무가설이 참이라고 가정할 때, 랜덤하게 선택한 표본에서 지금의 ˉX가 나올 확률을 계산하고 이 확률이 낮다면 귀무가설이 참이 아니라고 판단

• 가설검정 과정
  0. 귀무가설, 대립가설을 설정한다.
  1. 확률이 낮다는 기준점이 필요하다. 유의수준 α를 도입한다.
  2. P(ˉX >= k) <= α가 되는 k를 찾아야 한다.
  3. ˉX를 표준정규확률변수 Z로 변환한다. 이를 검정통계량이라고 한다.
  
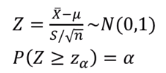
  4. ˉX를 Z로 변환한 후 Z값이 임계값(또는 기각역) z(a)보다 큰지를 검토한다.
  5. 크다면 귀무가설을 기각하고, 그렇지 않다면 귀무가설을 채택한다.
  

모평균의 검정

• 대립가설
  - 문제에서 검정하고자 하는 것이 무엇인지 파악이 필요하다.
  - 대립가설 채택을 위한 통계적 증거가 있어야 하며, 증거가 없으면 귀무가설을 기각할 수 없다.
  - H1: μ > μ0, μ < μ0, μ ≠ μ0

• 검정통계량
  - n >= 30인 경우: 중심극한정리 사용
  
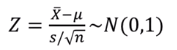
  - 모집단이 정규분포이고 모표준편차 σ가 주어진 경우
  
  

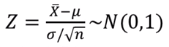
• 기각역
  

• 검정의 예
  - 어떤 농장에서 자신들이 생산하는 계란의 평균 무게가 10.5그램이라고 홍보하고 있다. 이 농장의 홍보가 맞는지 유의수준 5%로 검정하라.
  - 생산된 계란 30개의 표본을 뽑았더니 그 무게가 이와 같다.
  w = [10.7, 11.7, 9.8, 11.4, 10.8, 9.9, 10.1, 8.8, 12.2, 11.0, 11.3, 11.1, 10.3, 10.0, 9.9, 11.1, 11.7, 11.5, 9.1, 10.3, 8.6, 12.1, 10.0, 13.0, 9.2, 9.8, 9.3, 9.4, 9.6, 9.2]
  
  

교차엔트로피(Cross Entropy)

• 자기정보(Self-information): i(A)
  - A를 사건이라고 하면, i(A) = logb(1/P(A)) = -logbP(A) (밑이 b인 로그)
  - "확률이 높은 사건은 정보가 많지 않다"
  - 정보의 단위 b = 2(bits)
  - 자기정보의 특성: 두 사건이 동시에 일어났을 때 자기정보는 각각의 사건의 자기정보를 더한 것과 같다.
  

• 엔트로피(Entropy)
  - 엔트로피는 자기정보의 평균을 의미한다.
  
  - 사건의 수를 K라고 할 때, 0 <= H(X) <= log2K인 특성을 갖는다.
  - 엔트로피는 해당 정보를 표현하는 데 필요한 평균비트수를 나타낸다.
  

교차엔트로피

• 확률분포 P와 Q
  - P(Aj): (실제) 확률분포 P에서 사건 Aj가 발생할 확률
  - Q(Aj): (P를 추정한) 확률분포 Q에서 사건 Aj가 발생할 확률
  - i(Aj): 확률분포 Q에서 사건 Aj의 자기정보(Aj를 표현하는 비트수)
  - 잘못된 확률분포 Q를 사용하게 되면, 실제 최적의 비트수를 사용하지 못하게 된다.
  

• 교차엔트로피 H(P,Q)
  - 집합 S상에서 확률분포 P에 대한 확률분포 Q의 교차엔트로피
  - 확률분포 P에서 i(Aj)의 평균으로 정의한다. 확률분포 Q상에서 계산된 자기정보를 확률분포 P에 의해 평균을 낸다.
  
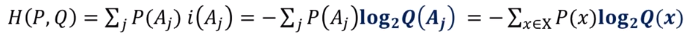
  - 이 값은 정확한 확률분포 P를 사용했을 때의 비트수보다 크게 된다. 따라서 P와 Q가 얼마나 비슷한지를 표현한다.
  - P와 Q가 같으면 H(P,Q) = H(P) 다르면 H(P,Q) > H(P)
  

• 분류 문제에서의 손실함수
  - 기계학습에서는 주어진 대상이 '각 그룹에 속할 확률'을 제공한다. 이 값이 정답(실제 속하는 그룹)과 얼마나 다른지 측정이 필요하다.
  - 분류 문제에서의 원하는 답은 P = [p1, p2, ..., pn]일 때 pi중 하나만 1이고, 나머지는 다 0인 것이다. 이 때 엔트로피 H(P) = 0이다.
  - pk = 1.0이라고 하면, qk의 값이 최대한 커지는 방향으로 학습을 진행한다.