[TIL Day9] 인공지능 수학 - 자료의 정리

인공지능 수학 - 자료의 정리

벡터와 직교분해

• 벡터의 내적
  
  - 두 벡터 u, v 간의 내적이 0이면 두 벡터는 직교(orthogonal)이다.
  - 직교의 물리적 의미: uㅗv일 때, u방향으로의 전진은 v방향에서 전혀 측정되지 않는다.
  

• 투영(Projection)
  - 두 벡터 u, a가 있을 때 벡터 u를 a 위에 투영한 벡터
  
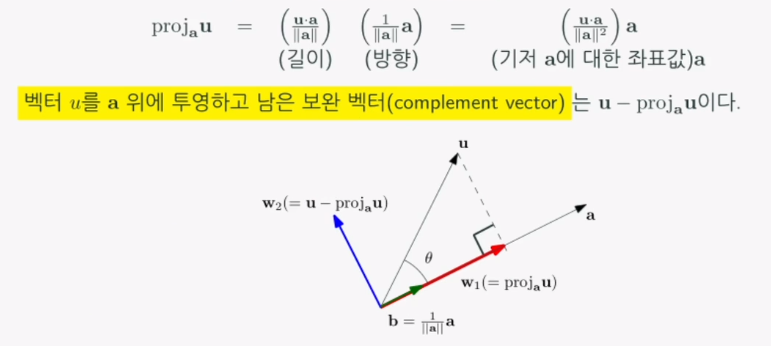
  - 투영과 보완은 서로 직교한다. 즉, 두 벡터 u, a가 있을 때, 투영과 보완의 개념을 이용해 직교분할할 수 있다.
  
• 직교행렬(Orthogonal Matirix): 직교좌표계에 대한 행렬 표현
  - 행렬은 각 열벡터가 기저(basis)를 이루는 좌표계이다.
  - 직교행렬: 주어진 행렬의 모든 열벡터가 서로 직교하는 행렬로, 직교행렬은 직교좌표계를 의미한다.
  - 정규직교행렬(Orthonormal Matrix): 주어진 행렬이 직교행렬이고 모든 열벡터의 크기가 1인 행렬로, 정규직교행렬은 정규직교좌표계를 의미한다.
  

• 직교행렬을 이용한 선형시스템
  - 선형시스템 Ax=b에서 행렬 A가 직교행렬이면, 해 x는 A의 역행렬 계산 없이 다음과 같이 구할 수 있다.
  • x의 i-번째 요소는 투영(projection)으로 계산할 수 있다. 즉, 벡터 b를 행렬 A의 각 열벡터 ai에 투영한 연산으로부터 xi를 계산할 수 있다.
  • x의 i-번째 요소와 j-번째 요소의 계산은 독립적이다. 즉, x의 계산은 병렬처리 가능하다.

• 정규직교행렬(회전행렬)을 이용한 선형시스템
  - 선형시스템 Ax=b에서 행렬 A가 정규직교행렬이면, 해 x는 A의 역행렬 계산 없이 다음과 같이 구할 수 있다.
  • x의 i-번째 요소는 내적으로 계산할 수 있다. 즉, 벡터 b를 행렬 A의 각 열벡터 ai에 투영한 연산으로부터 xi = b ⋅ ai 임을 계산할 수 있다.
  • x의 i-번째 요소와 j-번째 요소의 계산은 독립적이다. 즉, x의 계산은 병렬처리 가능하다.

• QR분해: 주어진 행렬에서 정규직교행렬 추출
  
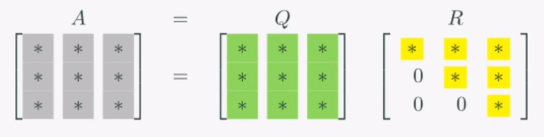
  - Q: 정규직교행렬(orthonormal matrix)
  - U: 상삼각행렬(upper triangular matrix)
  - QR분해를 이용하면 선형시스템을 두 단계로 간단히 해결할 수 있다.
  
  
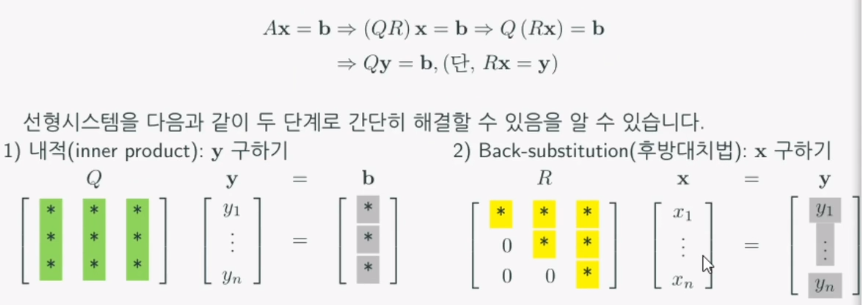
• QR분해의 활용
  - 빠른 계산: 선형시스템 Ax=b의 해를 구할 때, 정규직교행렬 Q를 이용한 계산 부분은 병렬처리로 빨리 계산할 수 있다. (R을 이용한 계산 부분은 병렬처리 할 수 없다.)
  - b가 자주 업데이트 되는 경우
  - Q행렬이 꽉찬 구조를 가진 행렬이므로 메모리 사용량이 많다.

특이값 분해(SVD; Singular Value Decomposition)

일반적인 m x n 행렬에 관한 행렬 분해로, 직교분할, 확대축소, 차원변환 등과 관련이 있다.

• 특이값 분해
  - 행렬을 회전과 확대축소로 분해하는 방법
  
  • U: m차원 회전행렬(정규직교행렬), 입력 차원인 R^m 공간에서의 회전
  • D: n차원 확대축소(확대축소 크기에 따른 정렬 형태), 입력 차원인 R^n 공간에 대해 축방향으로의 확대축소한 후, R^n → R^m 으로 차원 변환
  • V: n차원 회전행렬(정규직교행렬): 입력차원인 R^n 공간에서의 회전
    
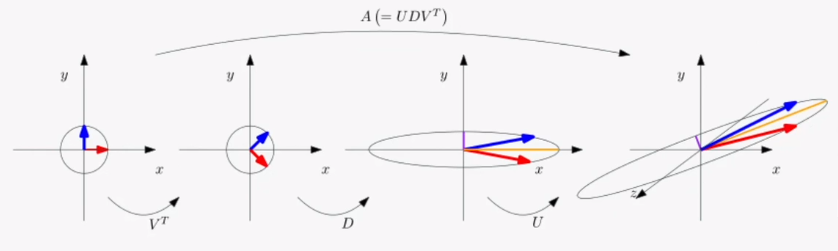
• 특이값 분해의 활용
  - A의 특이값 분해 U, D, V는 각각 열벡터의 순서대로 행렬 A의 열벡터가 어떤 방향으로 강한 응집성을 보이고 있는지 분석한 것
  - U, D, V의 열벡터를 순서대로 p개 취한다면, 강한 응집성을 가지는 p개의 방향으로 수선의 발을 내린 A의 근사치 A'를 재구성 할 수 있다.
  

주성분분석(PCA; Principal Component Analysis)

다수의 n차원 데이터에 대해, 데이터의 중심으로부터 데이터의 응집력이 좋은 n개의 직교 방향을 분석하는 방법

• 주성분분석
  - 데이터의 공분산행렬(covariance matrix)에 대한 고유값 분해에 기반을 둔 직교분해
  
  -W: n차원 회전행렬(정규직교행렬)
  -D: n차원 확대축소(확대축소 크기에 따른 정렬 형태)
  

벡터공간과 최소제곱법

• 집합(set)과 공간(space)
  - 연산에 닫혀 있는 집합: 어떤 연산을 생각한 다음, 집합에서 임의의 원소를 뽑아 연산을 수행한 결과가 여전히 집합의 원소로 있다면, 해당 집합은 연산에 닫혀 있다.
  - 공간은 다음의 두 연산에 닫혀 있는 집합이다.
  • 덧셈연산에 닫혀 있다.
  • 스칼라 곱 연산에 닫혀 있다.
  • 모든 n-벡터 집합 R^n은 n차원 벡터 공간(vector space)라 부를 수 있다.

• 열공간(Column Space)
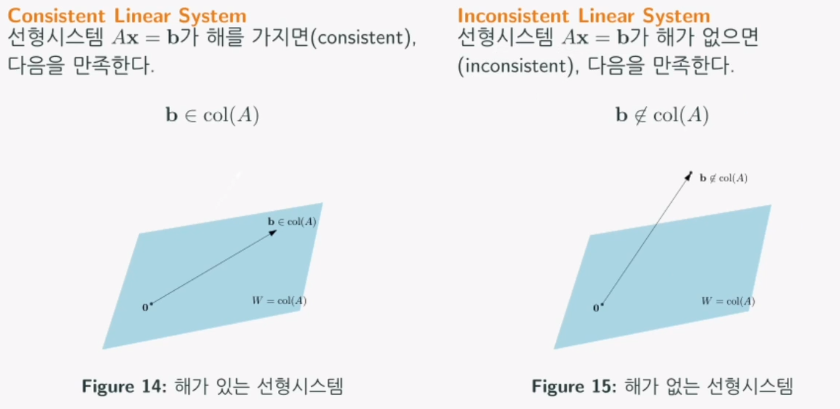
  - 행렬 A의 열벡터들에 대한 가능한 모든 선형조합의 결과를 모아 집합으로 구성
  

• 최소제곱법(Least Squares Method)
  - 선형시스템 Ax=b에 대한 해 x가 없음에도 불구하고, 할 수 있는 최선의 대안 ¯x을 내놓는 기법
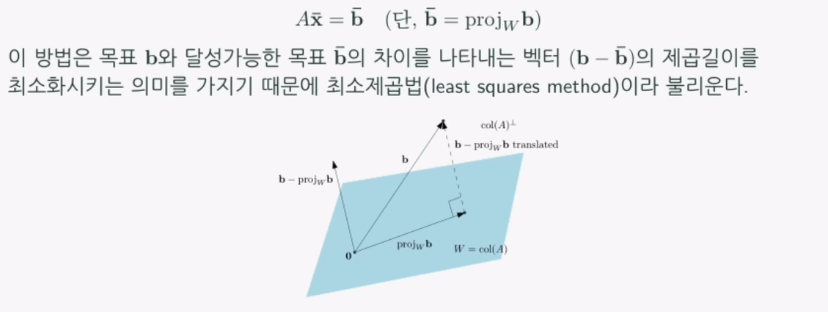
  - 행렬 A가 정의하는 열공간에서 우리의 목표 b와 가장 가까운 지점은 b를 열공간에 투영한 저점이다.
  
  

• 최소제곱법의 해 구하기
  - 주어진 선형시스템의 양변에 A의 전치행렬(transpose)을 곱하면 최소제곱법의 해를 구할 수 있다.
  

  • 최소제곱법으로 구한 해는 원래의 선형시스템을 만족하는 해는 아니다.

• 최소제곱법의 응용: 선형회귀(Linear Regression)
  1.선형시스템 구성
  - 직선이 각 정점을 모두 지나간다고 가정하고 선형시스템 Ax=b 구성
  - 단, 주어진 모든 정점을 지나가는 직선은 존재하지 않으므로 선형시스템의 해는 존재하지 않음.
  2. 최소제곱법 적용
  

통계학 기본개념

데이터의 수집, 구성, 분석, 해석, 표현에 관한 학문

• 개념 정의
  -모집단(population): 어떤 질문이나 실험을 위해 관심의 대상이 되는 개체나 사건의 집합
  - 모수(parameter): 모집단의 수치적인 특성
  - 표본(sample): 모집단에서 선택된 개체나 사건의 집합
  - 도수(Frequency): 어떤 사건이 실험이나 관찰로부터 발생한 횟수로, 도수분표표/막대그래프/히스토그램 등으로 표현한다.
  - 상대도수: 도수를 전체 원소의 수로 나눈 것
  

• 평균(Mean)
  - 모평균: 모집단 전체 자료일 경우
  - 표본평균: 모집단에서 추출한 표본일 경우
  - 극단 값의 영향을 많이 받는 단점이 있다.

• 중앙값(Median)
  - 주어진 자료를 높은 쪽 절반과 낮은 쪽 절반으로 나누는 값을 의미
  - 자료를 순서대로 나열했을 때 가운데에 있는 값
  - 자료의 수 n이 홀수이면, (n+1)/2번째 자료값
  - n이 짝수이면, n/2번째와 n/2+1번째 자료값의 평균
  

• 분산(Variance)
  - 편차(값과 평균과 차이)의 제곱의 합을 자료의 수로 나눈 값
  - 모분산: 자료가 모집단일 경우(N으로 편차의 제곱의 합을 나눈다.)
  - 표본분산: 자료가 표본일 경우(n-1로 편차의 제곱의 합을 나눈다.)

• 표준편차(Standard Deviation)
  - 분산의 양의 제곱근

• 범위(Range)
  - 자료를 정렬하였을 때 가장 큰 값과 가장 작은 값의 차이
  

• 사분위수(Quartile)
  - 전체 자료를 정렬했을 때 1/4, 1/2, 3/4 위치에 있는 숫자
  - 사분위범위(IQR, interquartile range): Q3 - Q1
  

• z-score
  - 어떤 값이 평균으로부터 몇 표준편차 떨어져 있는지를 의미하는 값