인공지능 수학 - 미적분
LU 분해
주어진 행렬을 특정한 형태를 가지는 두 행렬의 곱으로 나누는 행렬분해이다.
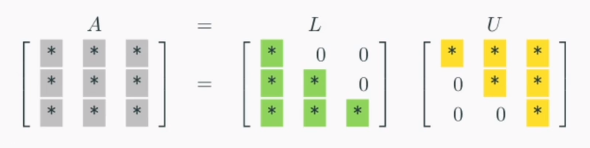
- L: lower triangular matrix(하삼각행렬)
- U: upper triangular matrix(상삼각행렬)
- 주어진 행렬 A가 LU분해되어 있으면 선형시스템을 다음과 같이 두 단계로 간단히 해결할 수 있다.
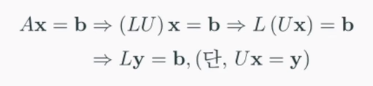
1. Forward-substitution(전방대치법): y 구하기
2. Back-substitution(후방대치법): x 구하기
- LU분해의 의미
- 가우스 소거법의 전방소거법을 행렬로 코드화 한 것이다.
-L: 행렬 A를 전방소거하는데 쓰인 replacement와 scaling에 대한 EROs를 기록해 둔 행렬
-U: 행렬 A를 전방소거한 후 남은 상삼각행렬
-P: 행렬 A를 전방소거하는데 쓰인 interchange에 대한 EROs를 기록해 둔 행렬(옵션)
- LU분해의 활용
- 수치적 안정성: 선형시스템 Ax=b의 해를 A의 역행렬을 이용해 직접 구하는 것 보다 PLU 분해를 이용하는 것이 좀 더 수치적으로 안정적이다.
- b가 자주 업데이트 되는 경우: 선형시스템 Ax=b에서 행렬 A는 고정되어 있고 b가 자주 변하는 문제가 종종 있다. 이런 경우, A를 미리 PLU로 분해해 둔다면, b가 업데이트 될 때마다 선형시스템의 해 x를 실시간으로 구할 수 있다.
행렬연산과 선형조합
- 행렬 표기법과 관련 용어
- 행렬(matrix): 직사각형 구조에 숫자들을 담아놓은 구조로, m x n 행렬은 (m x n)개의 숫자가 있는 형태
- 요소(entry): 각 숫자들은 행렬의 요소라 부른다.
- 행벡터(row vector), 열벡터(column vector): 하나의 행 혹은 하나의 열을 가지는 행렬
- 주요 표기법- 행렬 A의 각 (i, j)요소는 aij로 나타낸다.
- 행렬 A를 간략히 표기할 때는 A=[aij]로 나타낸다.
- 행렬 A의 크기가 중요할 경우는 A=[aij]mxn로 나타낸다.
-
전치행렬(Transpose Matrix)

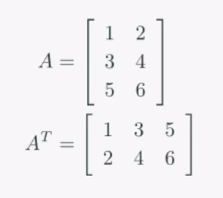
-
벡터 표기법
- 벡터라고 하면 일반적으로 열벡터를 말한다.
- 벡터는 볼드체 소문자로 표기한다.
- n-벡터는 n개의 스칼라(scalar)로 구성된 벡터를 말한다. -
영행렬(Zero Matrices)
- 행렬의 모든 요소가 0인 행렬
- 숫자의 0과 같은 존재로 행렬합에 대한 항등원 역할을 한다.
- 행렬의 합은 두 행렬 A와 B의 행과 열의 개수가 모두 같을 때 성립하여, 각 (i, j)요소의 합으로 정의된다.
-
정방행렬(Square Matrix)
- 행과 열의 개수가 모두 n인 정사각형 모향의 행렬을 n차 정방행렬이라 한다.
- 특히 aii(i = 1, 2, ..., n)를 행렬 An의 주대각선(main diagonal)이라 한다.
-
항등행렬(Identity Matrices)
- 주대각선이 1이고 나머지 요소는 모두 0인 n차 정방행렬을 항등행렬이라 한다.
- 항등행렬은 숫자의 1과 같은 존재로 행렬곱에 대한 항등원 역할을 한다.
-
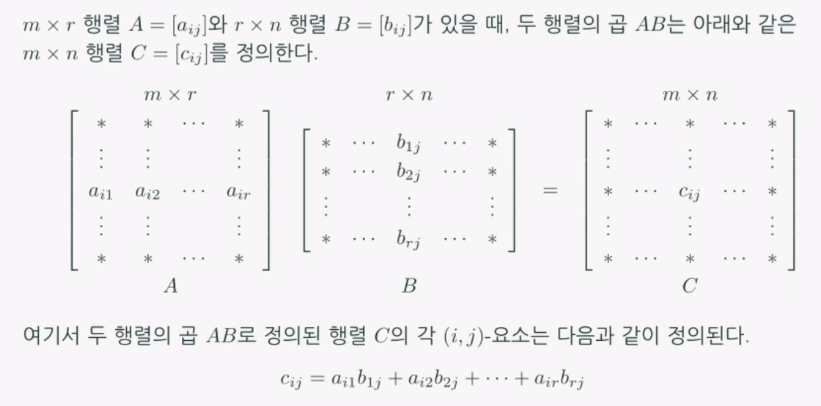
행렬의 곱
- 행렬 C의 각 요소 cij는 '곱의 왼쪽 행렬 A의 i번째 행벡터'와 '곱의 오른쪽 행렬 B의 j번째 열벡터'의 내적(inner product)이다.
- 따라서 두 행렬의 곱 AB에 대해 A의 열 개수와 B의 행 개수는 일치해야 한다.
- m x r 행렬과 r x n 행렬을 곱하면 m x n 행렬이 만들어진다.
- 일반적으로 AB≠BA이다. 행과 열을 뽑아오는 방법이 다르기 때문이다.
- 행렬의 곱은 병렬처리(parallel processing)로 가속할 수 있다.
-
스칼라, 벡터, 행렬, 그리고 텐서: 계층적 구조 이해하기
- 스칼라는 숫자 하나로 구성되어 있다.
- 벡터는 여러 숫자가 일렬로 늘어선 구조이다.
- 행렬은 사각형 구조에 여러 숫자가 행과 열로 늘어선 구조이다.
-
텐서(tensor)
- 스칼라, 벡터, 행렬을 아우르는 개념으로 숫자가 늘어설 수 있는 방향이 k개면 k-텐서로 부른다.
- 0-텐서: 스칼라, 1-텐서: 벡터, 2-텐서: 행렬, 3-텐서: RGB 컬러영상
-
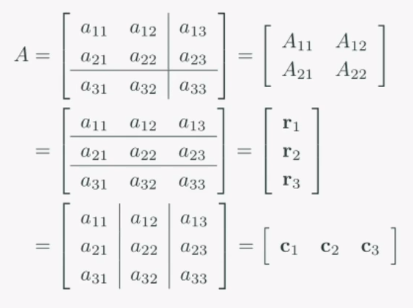
분할행렬(Partitioned Matrix)
- 행렬을 조각(partition) 단위로 분할하여 생각하자.
- 행렬은 부분행렬(submatrix)로 이루어진 직사각형 구조로 확장해서 생각할 수 있다.
- 행벡터 혹은 열벡터들의 집합이라고 볼 수 있다.
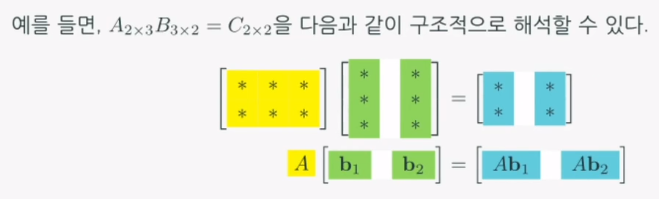
- 분할행렬로 행렬의 곱 이해하기- 두 행렬의 곱 AB=C를
matrix-column vector products혹은row vector-matrix products로 볼 수 있다.
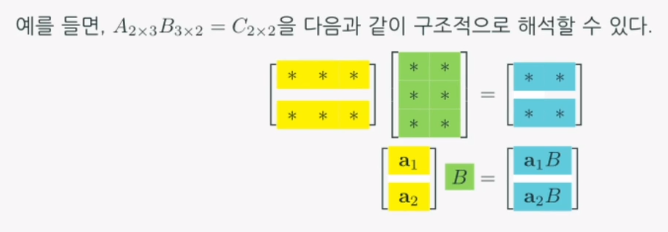
- 두 행렬의 곱 AB=C를
선형조합(Linear Combination)
Ax는 A의 열벡터에 대한 선형 조합
- 행렬을 구조적으로 보기
- 행렬은 열벡터의 리스트이다
-m x n 행렬은 m-벡터가 n개 있다고 해석하자.
- 행렬@벡터 연산을 구조적으로 보기
- Ax는 행렬 A가 가지고 있는 열벡터의 선형조합이다.
- 선형대수에서는 이처럼 벡터들에 대한 가중치 합을 특히 선형조합(linear combination)이라 부른다.
- Ax의 결과는 행렬 A가 가지고 있는 열벡터의 선형조합으로만 한계가 지어진다.

- 열공간(Column Space)
-col(A): 행렬 A의 열벡터들에 대한 가능한 모든 선형조합의 결과를 모아 집합으로 구성한 것
- 선형시스템 Ax=b가 해를 가지면(consistent), b∈col(A)
- 선형시스템 Ax=b의 해가 없으면(inconsistent), b∈col(A)
좌표계 변환(Change of Basis)
좌표계 :: 좌표값 = 행렬 :: 벡터
-
벡터의 수학적 표현
- 좌표계를 도입한 후, 벡터의 시작점을 원점에 맞추고 끝점의 위치를 벡터 v의 수학적 표현으로 정의한다.
- v의 크기: 화살표의 길이를 계산
- v의 방향: 화살표의 방향을 벡터로 표현 -
좌표계(Coordinate System)


- 선형시스템 Ax=b 문제를 좌표계 변환으로 바라보자
- (우항): 표준좌표계에서 어떤 벡터의 좌표값은 b이다.
- (좌항): A의 열벡터들을 기저(basis)로 가지는 좌표계에서는 동일 벡터의 좌표값은 x이다.
- 행렬은 좌표계이고, 벡터는 좌표값이다. - 임의의 v는 다양한 좌표계에서 표현될 수 있다.
- v (표준좌표계에서 표현된 v) = A (좌표계 A) @ [v]A (좌표계 A에서 표현된 v)
- 선형시스템 Ax=b 문제를 좌표계 변환으로 바라보자
선형변환(Linear Transformation)
-
함수에 대한 고찰
-함수: D의 각 원소 x가 C의 한 원소 y(=f(x))에 대응되는 두 집합 간의 맵핑룰(mapping rule)
-정의역(domain): 입력이 정의되는 집합 D
-공역(codomain): 출력이 정의되는 집합 C
-치역(range): 공역 중 실제 함수의 출력이 나오는 부분집합 -
선형함수(Linear Function)
- 함수 f가 아래 두가지 조건을 만족하면 이 함수를 선형함수라고 한다.
- f(x + y) = f(x) + f(y)
- f(cx) = cf(x) (단, c는 임의의 스칼라)
-
행렬변환(Matrix Transformation)
- 함수의 입출력이 벡터인 함수를 변환(transformation)이라고 한다.
- 입력이 n-벡터이고 출력이 m-벡터인 함수 T에서 특별히 n = m인 경우 해당 변환을 연산자(operator)라고 한다.
- m x n 행렬은 n-벡터를 입력으로 받아 m-벡터를 출력으로 내는 선형변환이며, 임의의 선형변환은 행렬로 표현가능하다. 즉, 행렬은 선형변환의 구현체이다. -
행렬변환 코딩하기
1. 구현하고자 하는 기능의 입/출력이 벡터로 정의되는지 확인한다.
2. 구현하고자 하는 기능이 선형인지 확인한다.
3. 입력이 n-벡터이고, 출력이 m-벡터이면 m x n 표준행렬(standard matrix)을 구성한다.

