변수 네이밍 규칙
- 영문 문자와 숫자 사용 가능
- underbar( _ ) 로 시작할 수 있음.
- 숫자부터 시작하면 안 됨.(문자부터 시작)
- 대소문자 구분
- 예약어(int, short, long 등) 사용 불가
변수 선언 방법
int number;
int a, b, c;
int num1 = 10;- 변수는 자료형 변수이름; 형식으로 선언
- 한번에 여러 변수를 선언할 수 있음(위 코드의 2번째 줄에서 a, b, c 세 개의 변수를 선언)
- 세번 째 줄 처럼 변수를 선언하며 값을 할당할 수 있음. 이를 "변수를 초기화한다"라고 표현
정수 자료형
- C언어는 저장할 값의 종류에 따라 자료형이 다름
예) 파이썬에서는 변수이름 = 데이터 형식으로 저장하지만, C언어에서는 변수를 선언한 후, 해당 변수의 타입과 범위에 맞는 데이터를 저장해야 함. - 숫자를 저장하는 변수의 경우 signed/unsigned 변수로 나뉨
- signed와 unsigned 변수는 양의 정수, 0을 모두 저장할 수 있으나 음의 정수는 signed 변수에서만 저장 가능
참고: 1byte=8bit
| 자료형 | 크기 | 범위 | 비고 |
|---|---|---|---|
| char signed char | 1byte(8bit) | -128~127 | |
| unsigned char | 1byte(8bit) | 0~255 | |
| short short int | 2byte(16bit) | -32,768~32,767 | int 생략 가능 |
| unsigned short unsigned short int | 2byte(16bit) | 0~65,535 | int 생략 가능 |
| int signed int | 4byte(32bit) | -2,147,483,648~2,147,483,647 | |
| unsigned unsigned int | 4byte(32bit) | 0~4,294,967,295 | int 생략 가능 |
| long long int signed long signed long int | 4byte(32bit) | -2,147,483,648~2,147,483,647 | int 생략 가능 [주의] OS별 크기가 다름! |
| unsigned long unsigned long int | 4byte(32bit) | 0~4,294,967,295 | int 생략 가능 |
| long long long long int signed long long signed lont long int | 8byte(64bit) | -9,223,372,036,854,775,808~9,223,372,036,854,775,807 | int 생략 가능 |
| unsigned long long unsigned long long int | 8byte(64bit) | 0~18,446,744,073,709,551,615 | int 생략 가능 |
정수형 변수의 사용
#include <stdio.h>
int main() {
unsigned char num1 = 200; //1바이트 부호 없는 정수형
unsigned short num2 = 60000; //2바이트 부호 없는 정수형
unsigned int num3 = 1234567890; //4바이트 부호 없는 정수형
unsigned long num4 = 4123456789; //4바이트 부호 없는 정수형
unsigned long long num5 = 1234567891234567890; //8바이트 부호 없는 정수형
printf("%u, %u, %u, %lu, %llu\n", num1, num2, num3, num4, num5);
return 0;
}200, 60000, 1234567890, 4123456789, 1234567891234567890
Operating System & Platform 에 따른 long의 크기
long을 사용할 때에는 OS와 Platform마다 byte가 다르므로 주의해야 함.
아래의 사진은 Ubuntu 64bit와 Windows 64bit에서 동일한 코드를 실행시켰을 때의 결과값으로, long의 크기가 다른 것을 확인할 수 있음.
| OS | CPU(Platform) | byte | bit |
|---|---|---|---|
| Windows | x86(32비트) | 4byte | 32bit |
| Windows | x86-64(64비트) | 4byte | 32bit |
| Linux | x86(32비트) | 4byte | 32bit |
| Linux | x86-64(64비트) | 8byte | 64bit |
| OS X | x86(32비트) | 4byte | 32bit |
| OS X | x86-64(64비트) | 8byte | 64bit |
정수형 자료형에서의 overflow와 underflow
#include <stdio.h>
int main() {
char num1 = 128;
unsigned char num2 = 128;
unsigned char num3 = 256;
printf(" signed char(num1): %d\nunsigned char(num2): %u\nunsigned char(num3): %u", num1, num2, num3);
return 0;
}signed char(num1): -128
unsigned char(num2): 128
unsigned char(num3): 0
char에 저장할 수 있는 최댓값: 127
unsigned char에 저장할 수 있는 최댓값: 255
signed char(num1)에는 127까지만 저장할 수 있는데, 127을 초과하였으므로 오버플로우가 발생하였고, unsigned char(num2, num3)에는 255까지만 저장할 수 있는데, 255를 초과하여 num3에서 언더플로우가 발생한 것을 확인할 수 있다.
자료형의 사이즈, 최솟값, 최댓값 확인
#include <stdio.h>
#include <limits.h>
int main() {
printf("[Size] char: %d, short: %d, int: %d, long: %d, long long: %d\n\n",
sizeof(char),
sizeof(short),
sizeof(int),
sizeof(long),
sizeof(long long)
);
printf("[Minimum] char: %d, short: %d, int: %d, long: %ld, long long: %lld\n",
CHAR_MIN, SHRT_MIN, INT_MIN, LONG_MIN, LLONG_MIN);
printf("[Maximum] char: %d, short: %d, int: %d, long: %ld, long long: %lld\n",
CHAR_MAX, SHRT_MAX, INT_MAX, LONG_MAX, LLONG_MAX);
return 0;
}[Size] char: 1, short: 2, int: 4, long: 4, long long: 8
[Minimum] char: -128, short: -32768, int: -2147483648, long: -2147483648, long long: -9223372036854775808
[Maximum] char: 127, short: 32767, int: 2147483647, long: 2147483647, long long: 9223372036854775807
참고: unsigned 정수 자료형의 최솟값은 모두 0이며 최댓값은 signed 자료형의 최댓값을 호출하는 매크로 상수(예: CHAR_MAX) 앞에 U를 붙이면 됨.
2진수 계산법
이진법: 두 개의 숫자(1과 0)만을 이용하는 수 체계
| 연산 | num1 | 기호 | num2 | result |
|---|---|---|---|---|
| 덧셈 | 0 | + | 0 | = 0 |
| 덧셈 | 0 | + | 1 | = 1 |
| 덧셈 | 1 | + | 1 | = 10 |
| 곱셈 | 0 | × | 0 | = 0 |
| 곱셈 | 0 | × | 1 | = 0 |
| 곱셈 | 1 | × | 1 | = 1 |
[참고] 10진수를 2진수로 변환하기
우리는 평소에 12345, 443, 80 과 같은 10진수를 사용해 숫자를 표시한다. 10진수를 2진수로 변환하려면 몫이 0이 될 때 까지 2로 나누면 된다.
156을 10진수에서 2진수로 변환하는 과정
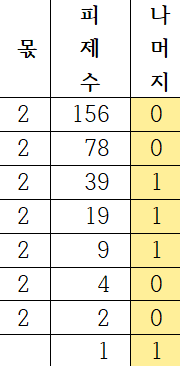 | 156을 몫이 0이 될 때 까지 2로 나누면 됩니다. 맨 아래를 보면 몫이 0이 되어있는 것을 확인할 수 있습니다. 몫이 0이 될 때까지 계산한 후 나머지를 아래에서 위로 읽으면 이진수가 됩니다. 따라서 156을 10진수에서 2진수로 변환하면 10011100 이 됩니다. |
|---|
음수 표현법
부호절대값(Sign Magnitude)
부호: MSB(Most Significant Bit)로 양수(0)과 음수(1)를 구분
크기: 나머지 bit로 크기를 표현
장점: 직관적이다
단점: +0과 -0이 존재하며, 양수의 덧셈과 음수의 덧셈을 다르게 해야함(1-2=-1: 0001+ 1010 = 1011?)
| 10진수 | 2진수 | 반대부호 | 2진수 | 10진수 |
|---|---|---|---|---|
| 0 | 0000 | -> | 1000 | 0 |
| 1 | 0001 | -> | 1001 | -1 |
| 2 | 0010 | -> | 1010 | -2 |
| 3 | 0011 | -> | 1011 | -3 |
| 4 | 0100 | -> | 1100 | -4 |
| 5 | 0101 | -> | 1101 | -5 |
| 6 | 0110 | -> | 1110 | -6 |
| 7 | 0111 | -> | 1111 | -7 |
1의 보수(1's complement)
부호: MSB(Most Significant Bit)로 양수(0)과 음수(1)를 구분
크기: 나머지 bit를 반전(0↔1)해서 같은 크기를 표현
장점: 양수의 덧셈과 음수의 덧셈이 같다.(1-5=-4: 0001 + 1010 = 1011) 단, 캐리가 발생하면 LSB에 1 더함(5-4=1: 0101 + 1011 = 10000 ↔ 0001)
캐리?
단점: 직관적이지 않고 +0과 -0이 존재
2의 보수(2's complement)
더해서 0이 되는 수(넘은 비트는 무시), 1 + (-1) = 0
모든 bit를 반전(0↔1)한 뒤, LSB에 1을 더한 수
장점: 0이 오직 하나, 여전히 MSB=1이면 음수, 음수 하나 더
장점: 양수와 음수의 덧셈이 같음 (5-4=1: 0101 + 1100 = 0001)
단점: 직관적이지 않다.
실수 자료형
- 실수는 부동소수점 방식으로 저장
- IEEE 754 표준 규약 (기수 = 2)
| 자료형 | 크기 | 범위 | 유효자릿수 | 비고 |
|---|---|---|---|---|
| float | 4byte (32bit) | 1.175494e-38~3.402823e+38 | 7 | <IEEE 754 단정밀도 부동소수점> 부호비트(Significant, 1bit): 양수(0), 음수(1) 부호비트(Significant, 1bit): 양수(0), 음수(1)지수부(Exponent, 8bit): -126 ~ 128, Bias 127 가수부(Mantissa, 23 Bit) 즉 부터 사이의 값 표현 가능 |
| double | 8byte (64bit) | 2.225074e-308~1.797693e+308 | 16 | <IEEE 754 배정밀도 부동소수점> 부호비트(Significant, 1bit): 양수(0), 음수(1) 부호비트(Significant, 1bit): 양수(0), 음수(1)지수부(Exponent, 11bit): -1022 ~ 1024, Bias 1023 가수부(Mantissa, 52 Bit) 즉 ~ 값 표현 가능 |
| long double | 8byte (64bit) | 2.225074e-308~1.797693e+308 | 16 | <IEEE 754 배정밀도 부동소수점> |
정수를 표현할 때는 명확하게 표현할 수 있지만, 실수는 두 정수 사이에 무한한 값이 존재할 수 있기에 정확한 값을 표현하기 힘들다.
실수를 표현하려면 일정 수준의 오차를 전제하여 다양한 표현을 한다.
예) 1과 2사이에는 실수 1.1 1.1911111 1.1111111111 1.223232422222 등 무한개의 실수가 존재
참고 - IEEE 754 표준 - 부동소수점 자료 표현 (float, double)
2016. 1. 12. 01:00
실수형 변수의 사용
알아둘 것!
- float는 숫자 뒤에 "f"를 붙임.
- double은 숫자 뒤에 아무것도 붙이지 않음.
- long double은 숫자 뒤에 "l"을 붙임.
- float와 double의 형식지정자: %f
- long double의 형식지정자: %lf
#include <stdio.h>
int main() {
float num1 = 0.1f; //float는 숫자 뒤에 "f"를 붙임.
double num2 = 3867.215820; //double은 숫자 뒤에 아무것도 붙이지 않음.
long double num3 = 9.3275131; //long oduble은 숫자 뒤에 "l"을 붙임.
//float와 double의 형식지정자: %f
// long double의 형식지정자: %lf
printf("%f %f %Lf\n", num1, num2, num3);
return 0;
}0.100000 3867.215820 9.327513
#include <stdio.h>
int main() {
float num1 = 3.e5f; //지수 표기법으로 30000을 표기
double num2 = -1.3827e-2; //지수 표기법으로 -0.013827을 표기
long double num3 = 5.21e+9l; //지수 표기법으로 521000000을 표기
printf("num1: %f\nnum2: %f\nnum3: %lf", num1, num2, num3);
return 0;
}num1: 300000.000000
num2: -0.013827
num3: 5210000000.000000
num1: 3.000000e+05
num2: -1.382700e-02
num3: 5.210000e+09
실수형 자료형의 사이즈, 최솟값, 최댓값 확인
- 지수 표시법(exponential notation)
- 정수 부분을 한 자리로 만들고 지수를 표시
- 실수e + 지수: 실수 * 10의 거듭제곱
- 2.1e+3은 2.1 * 1000 = 2100
- 실수e-지수: 실수 * (1/10 의 거듭제곱)
- 2.1e-2는 2.1 * (1/100) = 0.021
#include <stdio.h>
#include <float.h> //실수 자료형의 양수 최솟값, 최댓값이 정의된 헤더 파일
int main() {
float num1 = 0.0f;
double num2 = 0.0;
long double num3 = 0.0l;
printf("[Size] num1: %d, num2: %d, num3: %d\n",
sizeof(num1),
sizeof(num2),
sizeof(num3)
);
printf("[Minimum] float: %.40f, double: %e, long double: %le\n",
FLT_MIN,
DBL_MIN,
LDBL_MIN
);
printf("[Maximum] float: %.2f, double: %e, long double: %le\n",
FLT_MAX,
DBL_MAX,
LDBL_MAX
);
return 0;
}[Size] num1: 4, num2: 8, num3: 8
[Minimum] float: 0.0000000000000000000000000000000000000118, double: 2.225074e-308, long double: 2.225074e-308
[Maximum] float: 340282346638528859811704183484516925440.00, double: 1.797693e+308, long double: 1.797693e+308
실수형 자료형에서의 overflow와 underflow
#include <stdio.h>
#include <float.h> //실수 자료형의 양수 최솟값, 최댓값이 정의된 헤더 파일
int main() {
float num1 = FLT_MIN; //float 양수 최솟값
float num2 = FLT_MAX; //float 양수 최댓값
//float 양수 최솟값을 100000000.0으로 나누면 아주 작은 수가 되면서 언더플로우 발생
num1 = num1 / 100000000.0f;
//float 양수 최댓값에 1000.0을 곱하면 저장할 수 있는 범위를 넘어서므로 오버플로우 발생
num2 = num2 * 1000.0f;
printf("%e %e\n", num1, num2); //실수의 언더플로우는 0
//오버플로우는 무한대가 됨
return 0;
}0.000000e+00 inf
문자 자료형
- C언어는 정수 자료형 char에 문자 한 개를 저장
- char 자료형은 문자를 바로 저장하지 않고, 문자에 해당하는 정숫값을 저장함
| 자료형 | 크기 | 범위 | 비고 |
|---|---|---|---|
| char signed char | 1byte(8bit) | -128 ~ 127 | 문자 저장 |
| unsigned char | 1byte(8bit) | 0 ~ 255 | 바이트 단위 문자 저장 |
C언어에서는 문자를 작은 따옴표로 묶어서 표현함.
char c1 = 'a';작은따옴표는 문자 두 개 이상을 묶을 수 없음(아래 코드는 불가)
char c1 = 'Hello World';
ASCII Code
- 아스키 코드: 문자를 정수로 나타내는 규칙
- 65(0x41) ~ 90(0x5A)는 A~Z 알파벳 대문자
- 97(0x61) ~ 122(0x7A)는 a~z 알파벳 소문자
- 나머지 값들은 공백, 숫자, 특수문자, 제어문자 등
- 문자는 ASCII 코드 규칙에 의해 정수로 저장되므로 정수처럼 덧셈과 뺄셈 가능
#include <stdio.h>
int main() {
char c1 = 'a';
char c2 = 'b';
/* a의 아스키코드값: 97
*
* 아스키 코드 규칙에 의해 char에 정수로 저장되므로
* a의 아스키코드값(97)에 1을 더하면 98이 된다.
* 98은 b의 아스키코드값으로, 형식지정자(%c)를 통해
* 아스키코드 98을 출력하면 b가 출력된다.
*
* %d를 사용하면 정수 값, %x를 사용하면 16진수 값
*/
printf("%c, %d, 0x%x\n", c1 + 1, c1 + 1, c1 + 1);
//위와 동일하게 작용해 c가 출력된다.
printf("%c, %d, 0x%x\n", c2 + 1, c2 + 1, c2+1);
return 0;
}b, 98, 0x62
c, 99, 0x63
서식지정자
%c
%x -> 16진수 출력
#include <stdio.h>
int main() {
char c1 = 'a';
char c2 = 'b';
char newLine = '\n';
printf("%c%c%c", c1, newLine, c2);
return 0;
}참고: 제어 문자도 char에 저장할 수 있음.
| 10진수 | 16진수 | 문자 | 표기법 | 설명 |
|---|---|---|---|---|
| 10 | 0x0A | LF | \n | 개행, 라인 피드(Line Feed), 새 줄(new line), 줄바꿈 |
| 13 | 0x0D | CR | \r | 복귀, 캐리지 리턴(Carriage Return), 줄의 끝에서 시작 위치로 되돌아감 |
| 9 | 0x09 | TAB | \t | 수평 탭(horizontal tab) |
문자형 변수 선언
#include <stdio.h>
int main() {
char c1 = 'a';
char c2 = 'b';
printf("%c, %d\n", c1, c1); //a, 97('a'의 아스키코드값)
printf("%c, %d\n", c2, c2); //b, 98('b'의 아스키코드값)
return 0;
}a, 97
b, 98
