---

본 < 지능형 시스템 > 시리즈는 부산대 정보컴퓨터공학과 차의영 교수님의 '지능형 시스템' 강의에서 배운 내용을 바탕으로 작성합니다.

---

🥅 홉필드 네트워크

물리학자 존 홉필드가 제안한 신경망의 물리적 모델이다.
자신을 제외한 모든 유니트들 간에 양방향으로 상호 연결된 네트워크.

✔️ 특징

• ⭐️ 이전 알고리즘과 다르게 "고정된 가중치"를 이용.
  연결 가중치가 사전에 저장.
• state feedback은 상태가 반복적으로 수정될 수 있도록 사용.
• 반복은 에너지 함수를 최소화하기 위해 반복.
• 비동기적, 국소적 계산을 통해 전역적 최적화 (global optimization)

✔️ 응용

• 연산기억(associative memory), CAM(content addressable memory)
  ➡️ 기억된 정보의 일부분을 사용하여 나머지 정보에 접근한다.

✔️ 장단점

• 단점:
  ➡️ 응용분야에 있어서 네트워크의 성능이 많이 제한된다.
  ➡️ 제한된 용량과 연상 능력 (TSP 경우 도시가 10개 이내가 좋다.)
• 장점 :
  ➡️ 병렬 처리 구조
  ➡️ ⭐️⭐️ 기억 패턴수 M이 unit의 총수 N의 15% 내외에서 연상기억으로 잘 동작한다.

  M < 0.15 * N

• 대표 패턴이 중복되면 불안정(orthogonal)하다.

🥅 알고리즘

✔️ 원리

(1) 학습 패턴을 양극화(바이폴라)로 바꾼다.

'0' 이 정보의 손실을 낼 수 있기 때문에 
학습할 때 바이폴라로 바꾸는 것.

2) 학습 패턴에 대한 홉필드 넷의 가중치 행렬을 계산

가중치 행렬을 계산하고 나서,
네트워크의 threshold (세타) 를 계산

3) 계산된 가중치 행렬을 저장

4) 입력 패턴이 들어오면 저장된 가중치 행렬을 이용하여 입력 패턴에 대한 학습 패턴을 연상

입력패턴에 대한 "각각의 bit update"를 한다.

✔️ 예제

예제로 살펴보자.

두 벡터를 학습시키고 싶다고 하자.

• 학습벡터
  a(1) = 1 = [1110]
  a(2) = 3 = [1100]
• 입력벡터
  b = [0100]

아래를 구하시오.

• 풀이
  

🥅 에너지 함수 Energy Function

✔️ 에너지 함수?

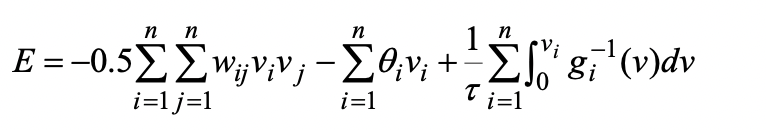
• 홉필드 네트워크은는dE/dt<=0 을 만족하는 한 에너지함수가 최소가 되어 안정구조로 수렴하게 된다.
• 이러한 형태의 에너지 함수에 대하여, 만약 각 neuron의 행위가 미분방정식에 의해 시간에 따라 변하면 net은 수렴하게 된다.

✔️ 예제

• (오타) 3개 뉴런 ➡️ 4개 뉴련

✔️ 풀이

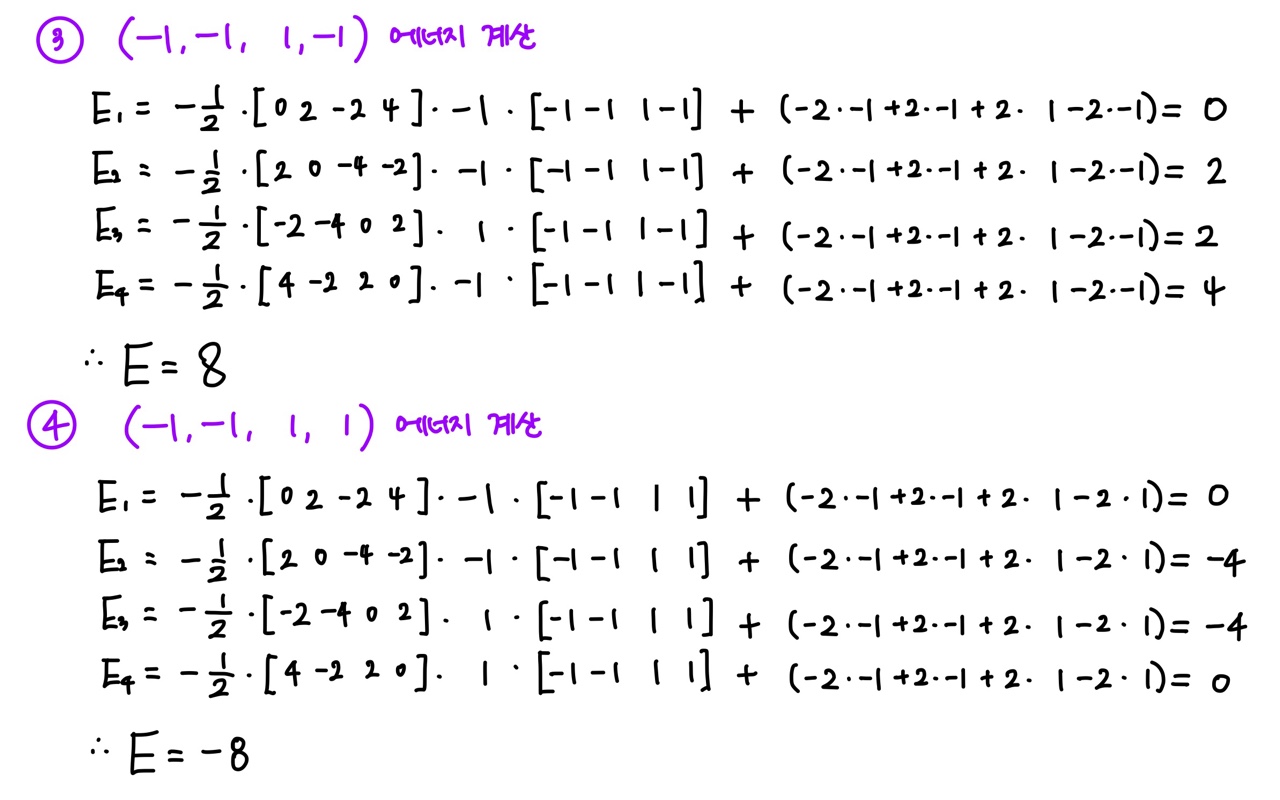
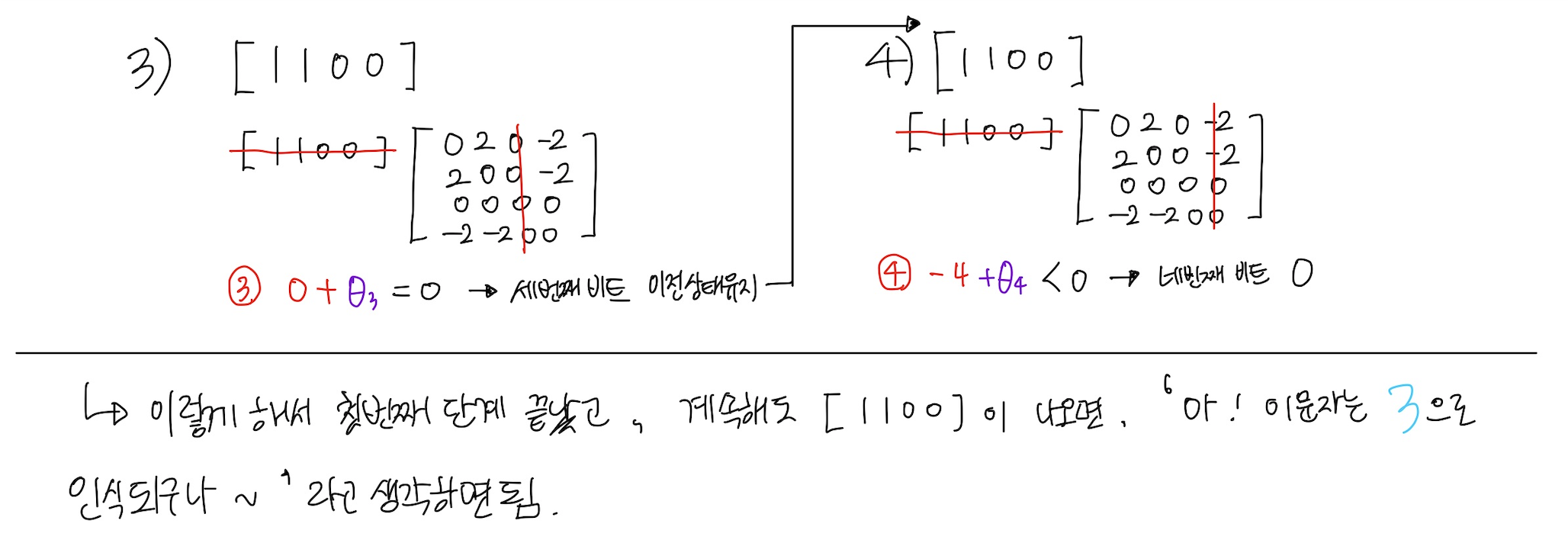
이렇게 해서 총 16개의 에너지 값을 계산하면, 아래와 같은 결과가 나오게 된다.

• 

---

👑 QUIZ

✔️ 문제

1. 영어 26개, 숫자 10개에 대해 "hopfield Net"를 쓴다면 최소 몇개의 뉴런이 필요한가?

2. 영어 26개, 숫자 10개에 대해 "퍼샙트론"을 쓴다면 최소 몇개의 뉴런이 필요한가?

✔️ 정답

1. 241 개
   ➡️ M < 0.15 * N 이므로 M/0.15 < N
   36 / 0.15 = 240 < N
   따라서 241 개이다.

2. 6 개
   ➡️ 36은 2의 5승 보다 크고 2의 6승보다 작기 때문에 최소 6개가 필요하다.

---

참고한 자료
https://untitledtblog.tistory.com/7