본 < 지능형 시스템 > 시리즈는 부산대 정보컴퓨터공학과 차의영 교수님의 '지능형 시스템' 강의에서 배운 내용을 바탕으로 작성합니다.
🧶 초기 퍼셉트론
Fank Rosenblatt 가 고안한 알고리즘이다.
다수의 신호(흐름이 있는)를 입력으로 받아 하나의 신호를 출력한다.
🧶 퍼셉트론의 학습 알고리즘
✔️ 원리
- weight와 threshold의 초기화
- input value에 대응되는 target value의 제시
- actual output 계산
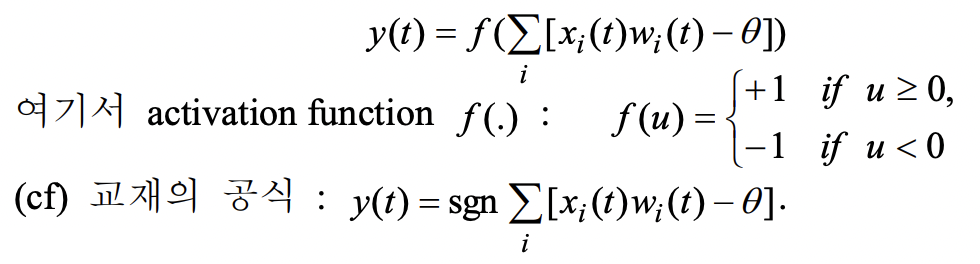
- weight 조정

- 여기서 "학습률"이 너무 크면 수렴이 안돼서 진동을 하고, 너무 작으면 수렴하는데에 무한대의 시간이 걸린다. 그래서 보통 0.001 정도로 학습률을 잡는다.
- d(t) 는 계산된 결과값, y(t)는 실제 결과값 이다.
- (3)으로 가서 desire output이 나올 때까지 반복하기
✔️ 예시
문자 “으”, “이”, “아”, “우”를 인식하는 신경망이 있다고 해보자.
이때, 4개의 문자가 입력될 때마다 아래 표처럼 인식 가능하게 학습한다고 하자.
초기가중치는 아래와 같다.
(지금은 손계산 편의성을 위해 다음과 같이 정의했지 실제로는 랜덤 넘버 generation을 해야한다.)4개의 문자의 입력 값과 희망하는 출력값은 아래와 같다.
손계산 편의성을 위해 학습률은 1로 가정한다.
(실제로는 0과 1사이 예를 들어 0.01 과 같은 수로 둬야함.)
1. 첫번째 학습
- 신경망에 "이" 입력하기

- 신경망에 "으"입력하기

- 신경망에 "아" 입력하기

- 신경망에 "우" 입력하기

2. 두번째 학습
3. 세번째 학습

- 이렇게 해서 모든 경우를 만족하는 최종 가중치를 구했다!
- 신경망 학습 끝.
= 지금까지의 위 단계를 학습 단계(learning phase).
= 실제 문자인식에 적용하는 것은 인식 단계(recognition phase).
🧶 퍼셉트론의 인식
방금까지 학습 단계를 통해 최종 가중치를 구했다.
실제 문자인식에 적용을 해보자.
아래 그림의 잡영이 들어간 문자를 벡터로 표현하면 [100000111] 이다.
이것을 최종 가중치와 곱해서 어떤 desired output이 나오는 지 살핀다.

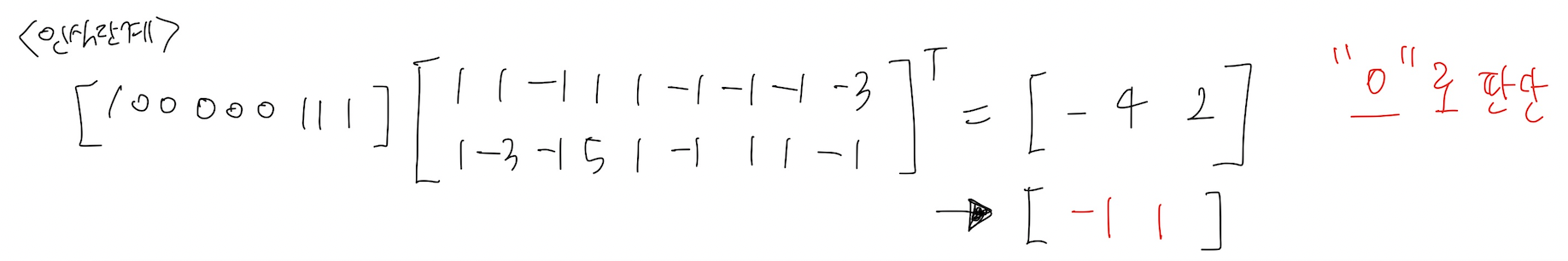
🧶 Single neural network 퍼셉트론의 한계와 극복
< 퍼셉트론의 한계 >
지금까지의 이 퍼셉트론은 Single neural network이다. 이것의 가장 대표적인 문제점은 XOR problem 이다.
아래와 같은 퍼셉트론이 있다고 할 때 Net 값을 식으로 표현할 수 있다. 이때 Net 값을 세타라고 두고 식을 y에 대해 고치면 일차 방정식 (직선) 이 나온다.
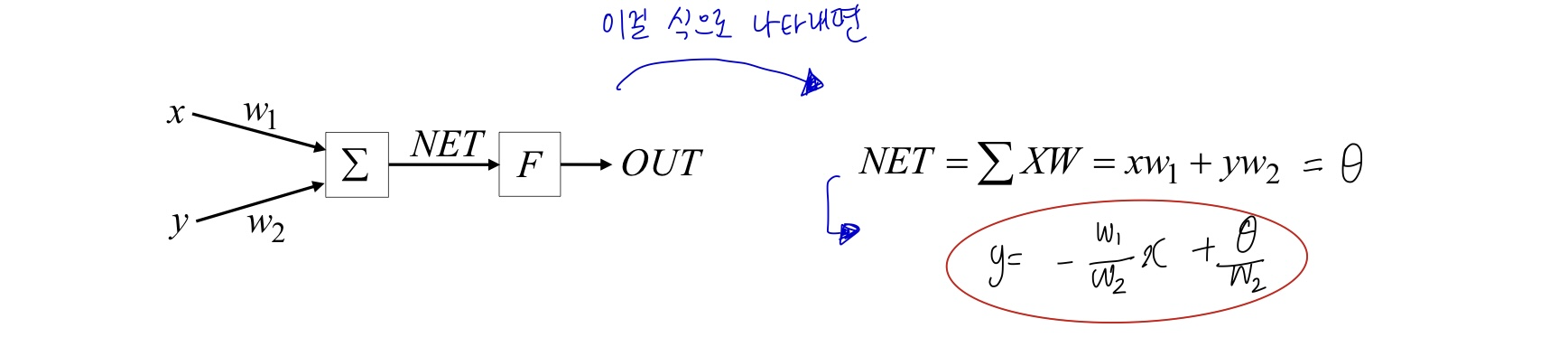
x,y 값에 따른 출력값이 다음과 같다고 할 때, 우리는 직선 하나만 가지고 0 영역과 1영역을 분류하지 못한다.
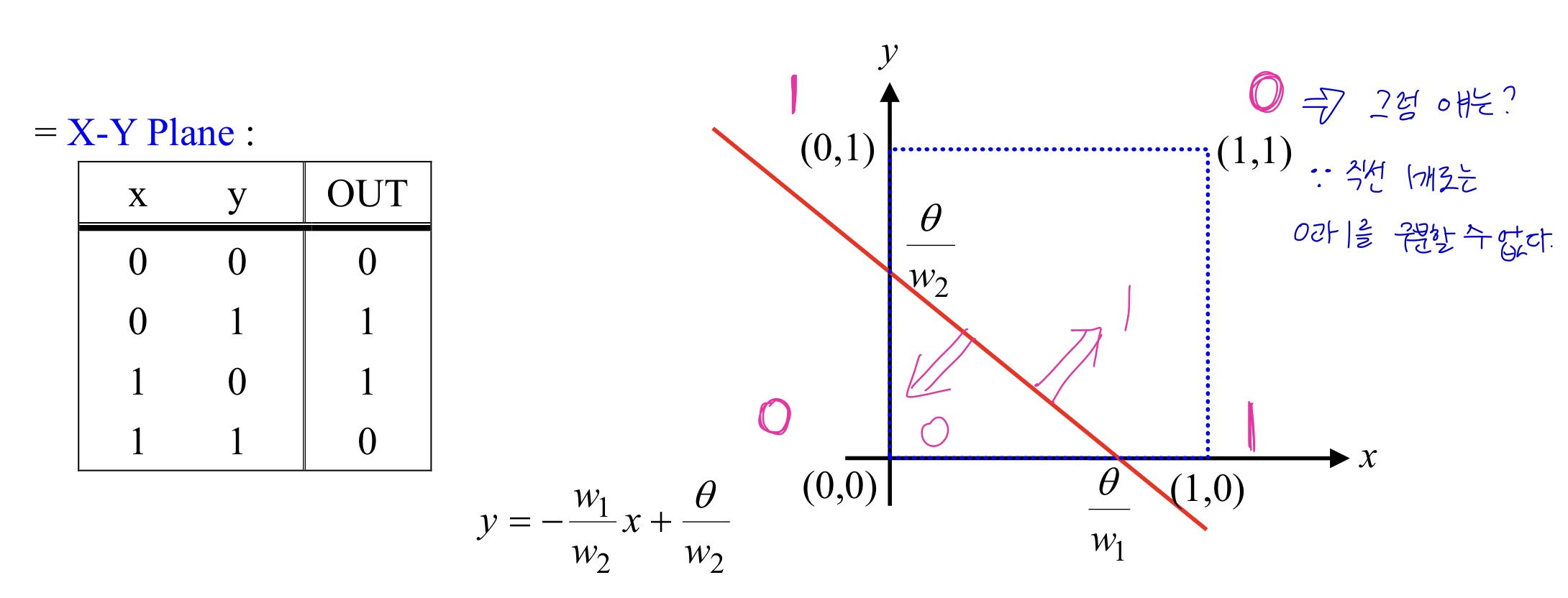
이 "선형 구분의 제한"이 바로 퍼셉트론의 한계라는 점이다.
< 퍼셉트론의 한계점 극복>
- 계층을 더한다.
➡️ 그럼 two-layer network가 된다.
볼록한 구역에 대한 분류가 가능해짐. - 계층을 한번 더 더한다.
➡️ 그럼 three-layer network가 된다.
오목한 구역에 대한 분류까지도 가능해짐.
🧶 아달린 (Adaline)
- Bernard Widrow 와 Marcian Hoff 이 향상 시킨 퍼셉트론을 발표함.
- Adaline (Adaptive Linear Neuron)
Madaline (a network of multiple Adalines)
앞서 설명한 Rosenblatt 의 퍼셉트론에서 사용하는 식과는 약간의 다른 식을 사용한다.
➡️ 학습 규칙
- 초기 퍼셉트론과 달리 활성화 함수 (sgn 함수)를 사용하지 않는다.
- 그래서 가중치 수정이 계속적으로 일어나고, 정보의 손실을 막을 수 있다.
- Widrow 와 Hoff 는 '시험값과 훈련값 사이의 오류' 제곱 합을 최소화 하도록 시스템이 생성한다는 것을 수학적으로 증명.
➡️ 이게 바로 최소 평균 제곱법이다 !
🧶 최소평균제곱법(Least Mean Squares Law)
✔️ 개요
Error = e1 + e2 + e3 + e4 = (d1 – y1) + ... + (d4 – y4)라고 했을 때 이대로 error를 구하면 각 뉴런에서의 error가 서로 상쇄되어 버린다.
이것을 방지하기위해 절대값을 취하거나 제곱을 한다.
그리고 미분에 대비하기위해 식에 1/2을 추가하는데, 이 모양이 평균 공식과 비슷하고, error를 최소화하는 방향으로 나아간다. 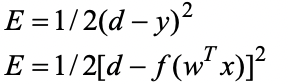
✔️ 예시
아래와 같이 모든 경우를 만족할 때까지 가중치를 구해나간다.



👑 Quiz
<문제>
(Single-layer 신경망의 입장에서) 신경회로망의 설계시,
0-9 까지의 숫자를 학습할려고 하고 숫자의 해상도가 8*6 크기라면..

- 입력단의 크기는 ?
- 필요한 뉴런의 개수는 ?
- W 행렬의 크기는 ?
<답>
- 8X6 = 48
- 4
0-9까지 10개의 숫자를 학습하려고 한다.
10은 2의 3승보다 크고 2의 4승 보다 작으니 필요한 뉴런의 개수는 4개이다. - 48 * 4 ( 입력단 크기 X 뉴런의 개수 )





