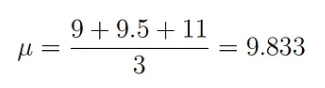Probability vs Likelihood
- 가장 먼저 likelihood의 정의에 대해서 알아야 합니다.
- probability: 확률 분포가 고정되어 있을 때, 어떤 사건이 일어날 가능성
- 고정된 확률 분포에 대한 파라미터에서 특정 데이터가 등장할 가능성
- 동전 던지기(확률 분포 고정)에서 앞면이 나올 가능성은 50%
- likelihood: 데이터가 주어졌을 때, 이 데이터들을 설명하는 확률 분포의 파라미터가 특정 값일 가능성
- 데이터들이 주어졌고, 확률 분포 모델이 정해졌을 때, 특정 분포 파라미터가 이 데이터들을 얼마나 잘 설명하는가
- 동전을 10번 던져서 7번이 앞면이 나왔다면, 확률 분포(50:50)이 아닐 수 있음
- 어떤 확률 분포의 파라미터를 찾는 데에 사용됨
Maximum Likelihood Estimation
- 데이터들이 주어지고 확률 모델을 정했을 때, 이 데이터들을 가장 잘 설명할 수 있는 모수(parameter)를 찾는 것입니다.
- Likelihood Function
- 확률 분포의 모수(parameter)를 input으로 받아서 각 데이터가 등장할 확률을 뱉는 함수입니다.
- 데이터에 가장 알맞은 모수(parameter)를 넣는다면 이 확률은 높게 나올 것입니다.
Maximum Likelihood Estimation 진행 과정
-
들어가기에 앞서 몇 가지 가정을 하겠습니다.
- 데이터들은 모두 독립적으로 생성된다.
- 확률 분포는 Gaussian distribution이다.
-
먼저 수식은 아래와 같을 것입니다.
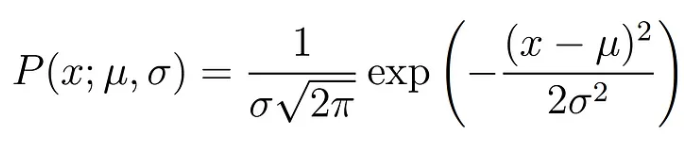
-
모든 데이터는 독립적이기 때문에, 데이터가 3개 있다고 가정하면 특정 파라미터에서 3개의 데이터가 등장할 확률은 각각의 확률을 곱한 것과 같습니다.
-
데이터 3개가 x: (9, 9.5, 11)이라고 가정해봅시다. 가우시안 분포로 확률 모델을 설정했기 때문에, 파라미터는 평균과 표준편차입니다.
-
따라서, likelihood function인 위의 수식에 각각의 데이터를 넣고 곱하면 최종 확률이 나오게 됩니다.
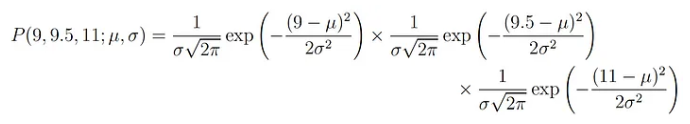
-
이제 해야 할 일은 이 값을 최대로 만드는 평균과 표준편차를 구하는 일입니다.
-
우리가 아는 최대값을 구하는 방법은 극값을 구하는 것이고, 이는 미분을 통해 구할 수 있습니다.
-
즉, 최대값인지 검증하는 과정은 거쳐야겠지만, 위의 식을 미분했을 때 0이 되는 평균과 분산이 Maximum Likelihood Estimation의 결과입니다.
Log likelihood
- 보통 MLE를 계산할 때에는 log likelihood로 변환하여 계산합니다. 그 이유는 아래와 같습니다.
- 곱셈보다는 덧셈
- 최종 확률을 위해서는 모든 데이터에 대한 확률값을 곱해야 합니다.
- 데이터가 많다면 이 확률값은 매우 작아질 수 있고, 소수점 이하 값들이 사라질 수 있습니다.
- log를 씌운 함수를 활용하면 곱셈이 덧셈으로 변환되므로 수치적으로 안정적입니다.
- 계산 효율성
- 가우시안 분포 곱셈을 보면 미분하기 매우 어렵습니다.
- 덧셈 자체가 계산적으로 더 쉽기 대문에 효율적입니다.
- 극점 유지
- log함수는 단조 증가함수이므로 적용하더라도 극값은 변하지 않습니다. 따라서 최적화 과정에서 문제가 없습니다.
-
다시 위의 식으로 돌아와서, log 함수를 적용해보면 아래와 같습니다.
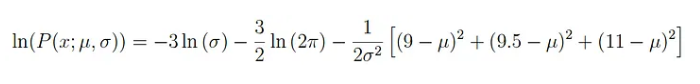
-
이제 극값을 찾기 위해 미분해야 합니다. 먼저 평균을 구하기 위해 평균에 대해 편미분하면 아래와 같습니다.
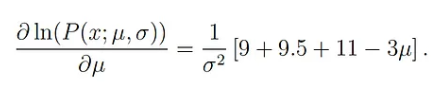
-
이제 이 함수가 0이 되는 극값을 찾으면 Maximum Likelihood Estimation의 전 과정을 마친 것입니다.