2.0 Linear Algebra

이 시리즈는 Mathematics for Machine Learning의 내용을 번역 및 재해석해서 작성한 글입니다. 이 책의 내용에 이해를 돕는 글을 첨부하였으며 완전한 번역본이 아님을 알려드립니다.

Linear Algebra

Vector symbol and their Operations
직관적인 개념을 공식화 할 때, 수를 지칭하는 대상을 기호화하고 대상 간의 작용(operation) 을 만듭니다. 대수(Algebra)라고 불리기도 하는데, 이 중 Linear Algebra는 vector와 vector를 계산하는 작동 방식에 대해 배웁니다. 일반적으로 벡터는, 서로 더하거나, 실수를 곱하여 같은 타입의 벡터를 생성할 수 있습니다. 그리고 벡터로 표현될 수 있는 몇 가지 예를 보겠습니다.

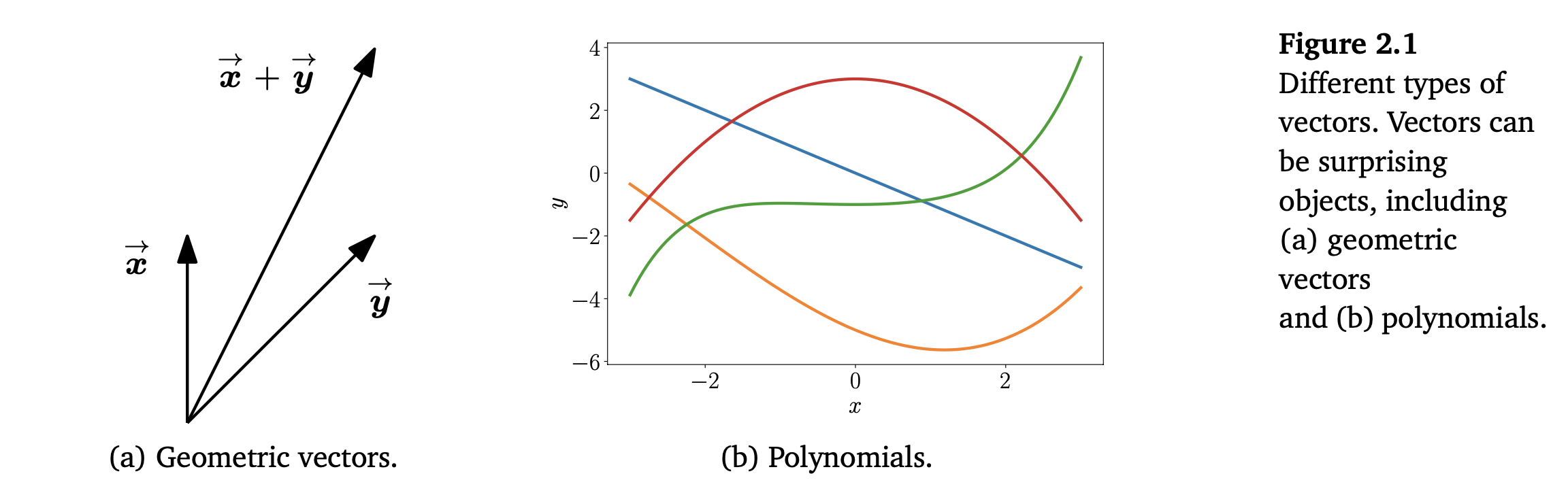
1. Geometric Vector
   아래처럼 서로 더해지고 실수곱이 가능하기 때문에 표현되기도 합니다.

2. Polynomials are also vectors
   Geometric vetor보다 자주 사용하진 않지만 서로 더해지고 실수곱이 가능하기 때문에 표현되기도 합니다.

3. Audion Siganls are vectors

4. Elements of $R^n$ (tuples of n real numbers) are vectors.

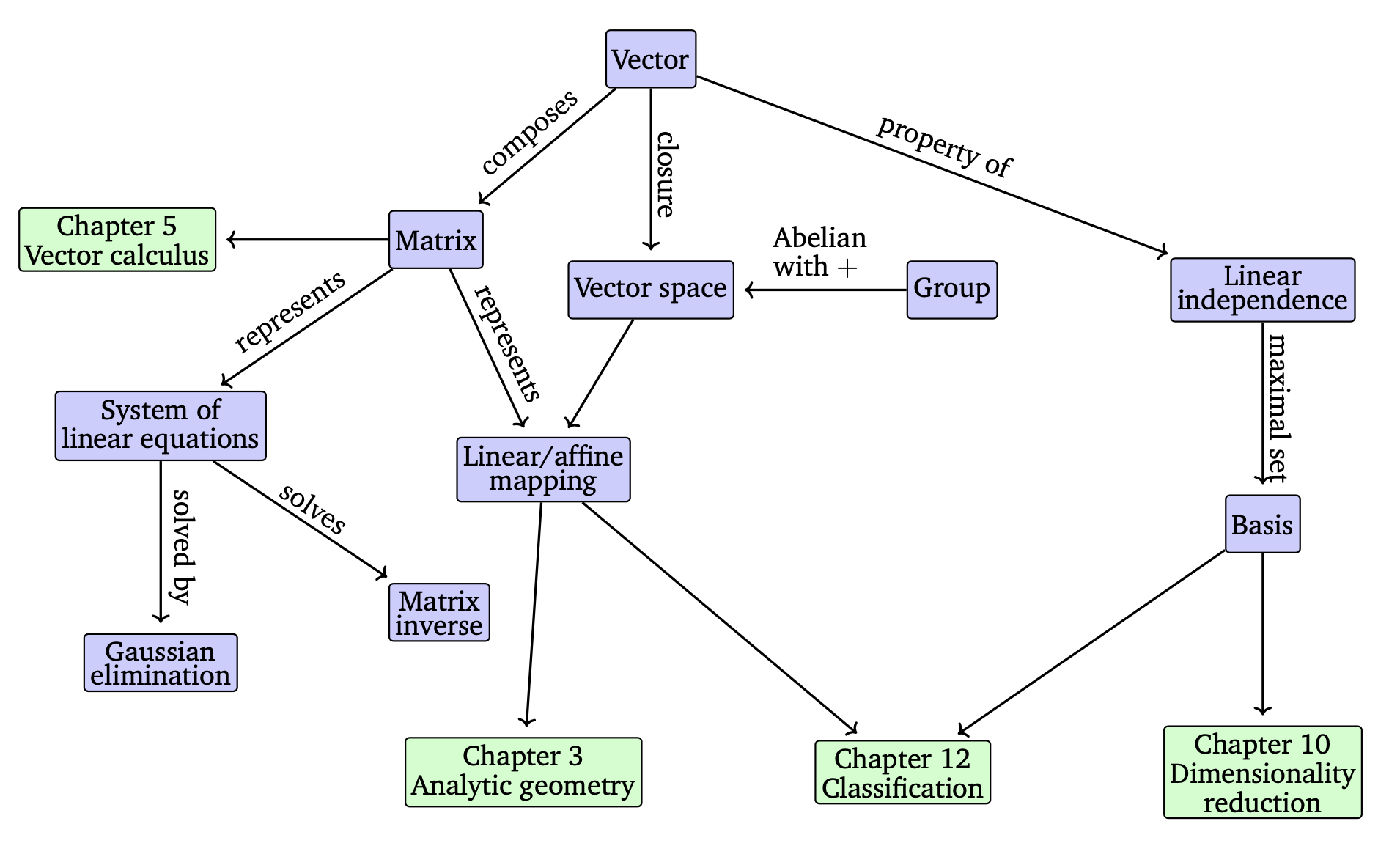
closure

$\vec{x}+\vec{y} = \vec{z}$에서 $\vec{x},\vec{y}$를 연산(operaction)하여 나온 작업물 $\vec{z}$ 은 어느 집합에 속하게 될까요? 벡터인 경우에는, 몇 개의 벡터로 이루어진 Small Set으로부터 서로 더해지고, 실수 배 연산을 통해 초기의 작은 Set과 Operation은 결국 Vector Space가 됩니다. Closure의 특징과 Vector Space는 (2.4)에서 다루도록 하겠습니다.

Contributor

Matt J
맹준영